Особенности работы гирокомпаса при стационарном движении судна

В рассматриваемом случае ускорения относительного движения судна и порождаемые его качкой, равны нулю. Кроме этого, будем учитывать то обстоятельство, что период прецессионных колебаний чувствительного элемента гирокомпаса, составляющий десятки минут, значительно больше постоянной времени акселерометра, которая, например, в гирокомпасе “Вега” не превышает одной минуты. Указанное обстоятельство позволяет опустить из рассмотрения первое слагаемое третьего уравнения исходной системы (3.9), определяющее динамические параметры акселерометра. В результате эта система уравнений примет следующий вид:

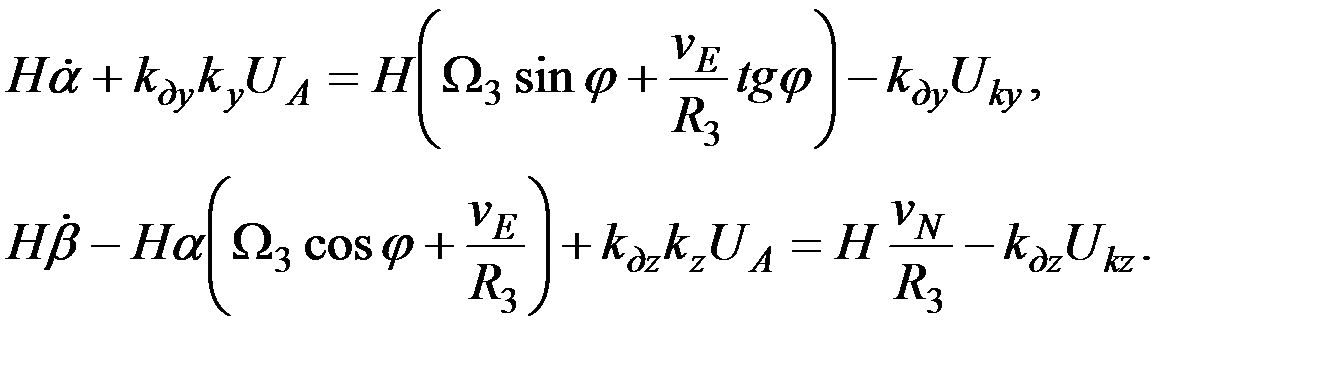
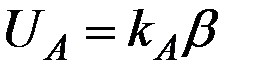. (3.10)

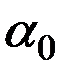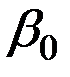Полученная система уравнений является неоднородной с постоянными коэффициентами. Решение этой системы складывается из общего решения и однородной системы

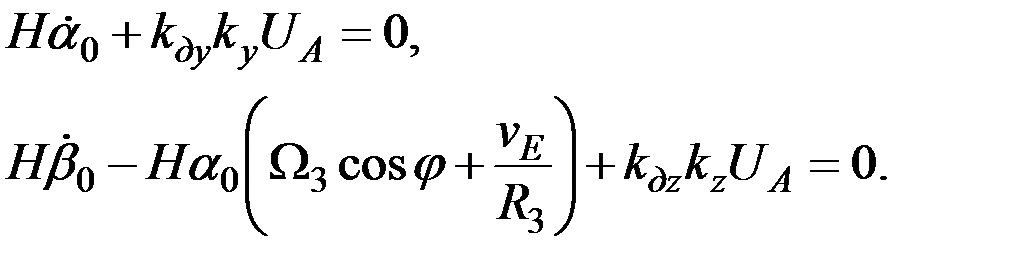
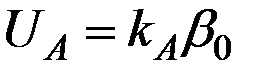(3.11)

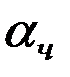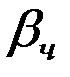и частного и решения неоднородной системы, в которой, учитывая практическую неизменность во времени значений правых частей исходного уравнения, можно опустить члены, содержащие 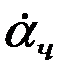и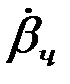

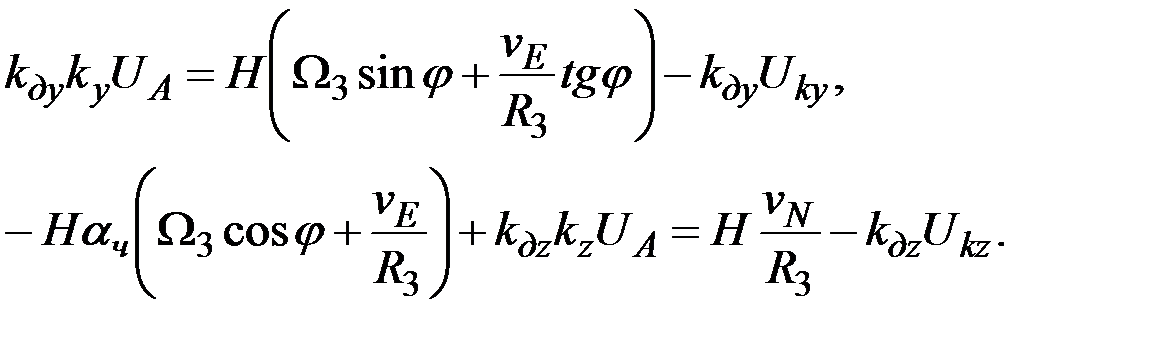
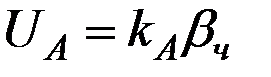. (3.12)

Определим вначале частное решение системы, характеризующее положение главной оси гироскопа после того, когда прекратятся все переходные процессы.

Для этого подставим третье уравнение системы (3.12) в первые два уравнения. В результате получим:

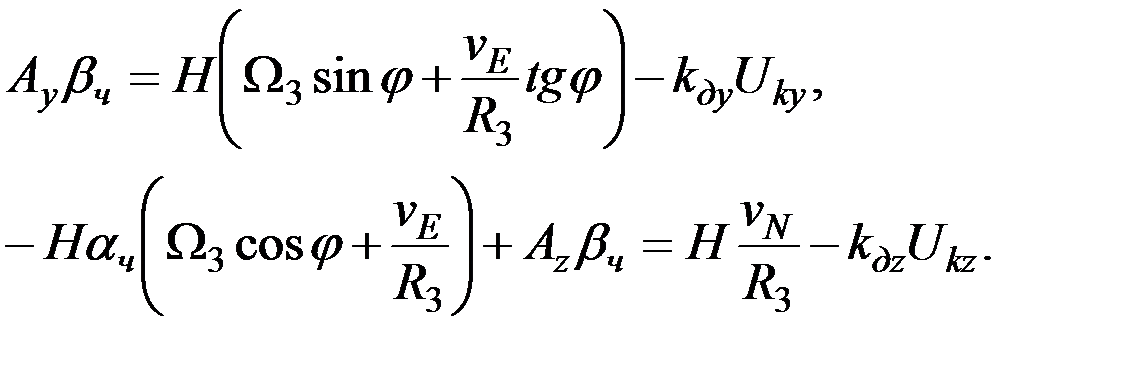(3.13)

где , .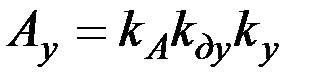

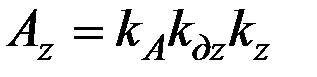Равенства (3.13) свидетельствуют о том, что при отсутствии сигналов U_ky и U_kz, вырабатываемых внешними системами коррекции,

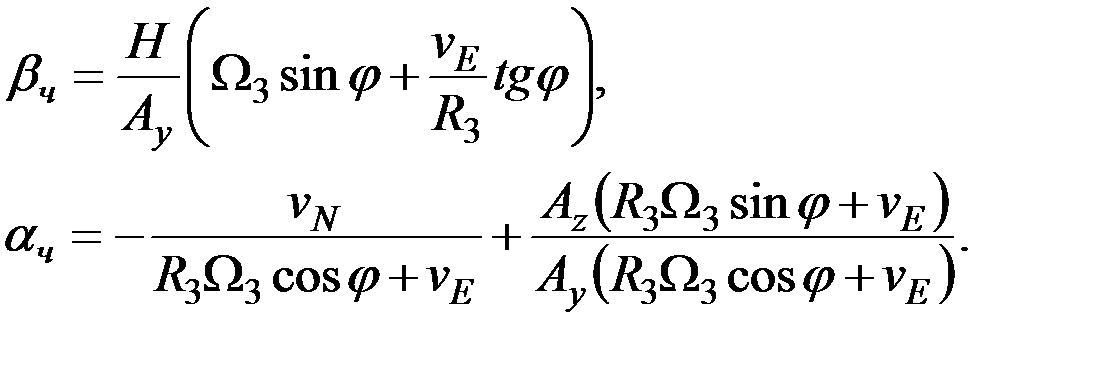(3.14)

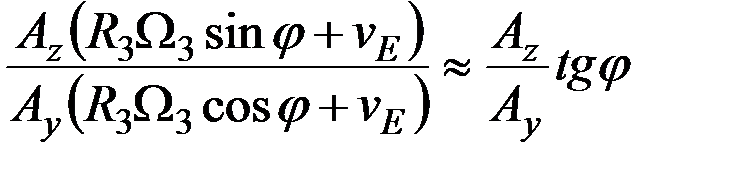Сравнивая полученные выражения с аналогичными выражениями (2.23) для двухгироскопного компаса, замечаем, что установившееся отклонение α_ч главной оси гирокомпаса от направления меридиана содержит кроме скоростной девиации составляющую

. (3.15)

Приближенное равенство в (3.15) возможно ввиду малости v_E по сравнению с R₃Ω₃. Эта составляющая, называемая широтной девиацией, обусловлена выбранным способом гашения прецессионных колебаний гироскопа и становится равной нулю, если разорвать контур демпфирования, т.е. сделать .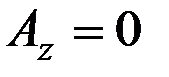

Что касается угла β_ч отклонения главной оси гироскопа от плоскости горизонта, то он в точности соответствует аналогичной координате двухгироскопного компаса с учетом того, что роль модуля 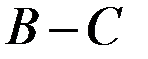играет .

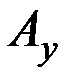Как нетрудно заметить из уравнений (3.13), можно сформировать сигналы U_ky и U_kz коррекции гироскопа таким образом, чтобы углы α_ч и β_ч стали равными нулю при любых стационарных параметрах движения судна. Для этого необходимо выполнить следующие условия:

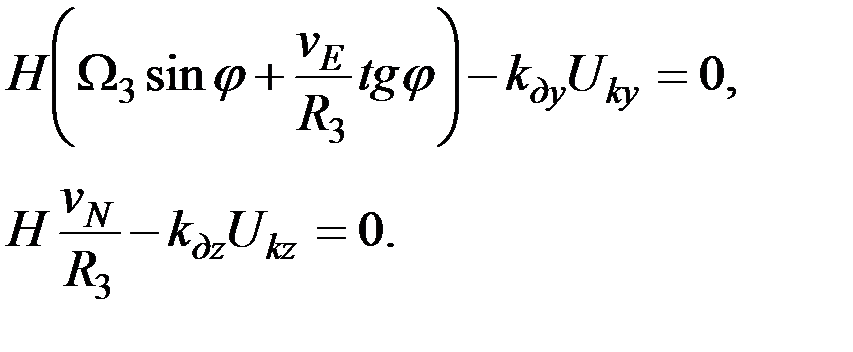
(3.16)

Последние равенства будут иметь место, если

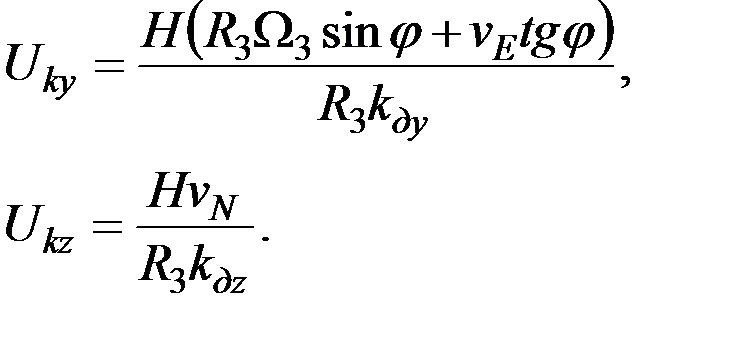(3.17)

Для формирования указанных напряжений необходима внешняя информация о скорости движения судна и широте его места. Информацию о курсе судна, требуемую для определения v_N и v_Е, снимают с датчика курса гирокомпаса.

Перейдем к анализу собственного движения главной оси гироскопа. Для этого обратимся к уравнениям (3.11). Если подставить третье уравнение названной системы в первые два уравнения, то они примут следующий вид:

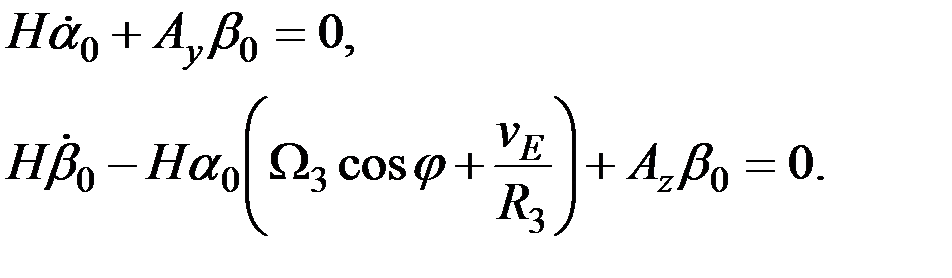(3.18)

Запишем характеристический определитель этих уравнений, составленный из коэффициентов левой их части: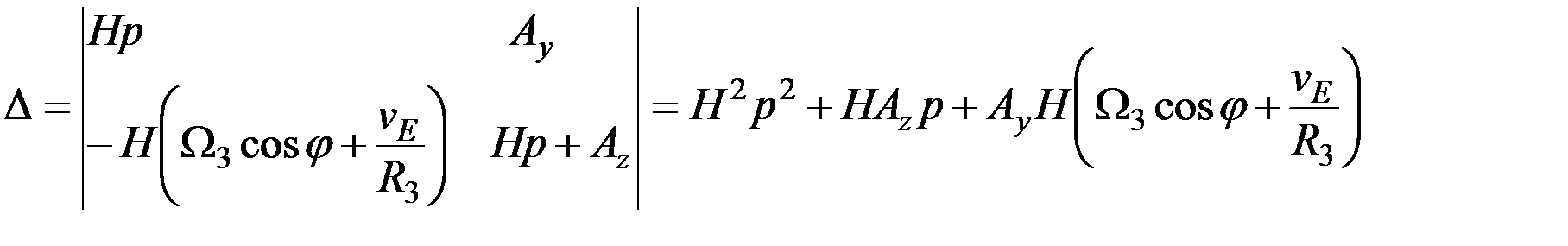

(3.19)

В силу того, что определители для переменных α и β равны нулю, уравнения для этих переменных будут идентичны. Так, уравнение для α примет вид:

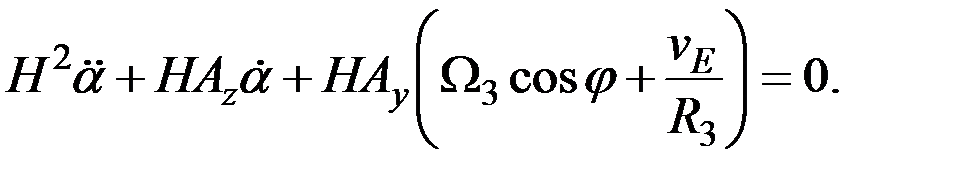(3.20)

Если поделить все его слагаемые на коэффициент при первом члене, то оно приобретет стандартную форму:

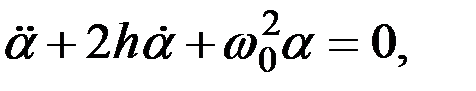(3.21)
где

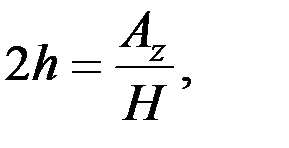(3.22)

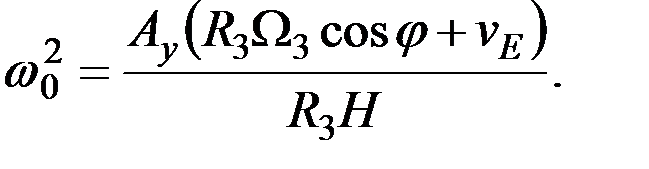(3.23)

Используя последнее выражение найдем период Т₀ незатухающих колебаний оси гироскопа:

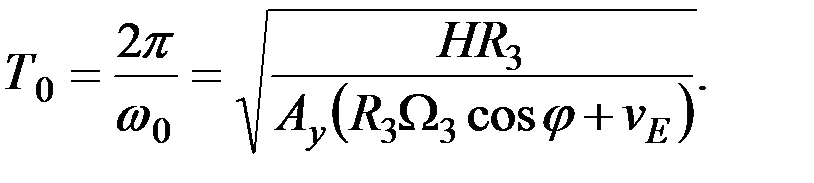(3.24)

Полученное выражение аналогично выражению для периода незатухающих колебаний гирокомпаса с непосредственной коррекцией. Как и ранее, этот период зависит от широты места судна и скорости его движения.

Общее решение уравнения (3.21), как известно, имеет вид

(3.25)
где q – частота затухающих колебаний гироскопа, определяемая выражением

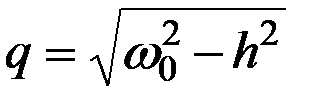, (3.26)

С₁ и С₂ – произвольные постоянные интегрирования, зависящие от начальных условий. Если сигналы коррекции U_ky и U_kz подобраны таким образом, что выполняются условия (3.16), закон изменения угла α примет вид:

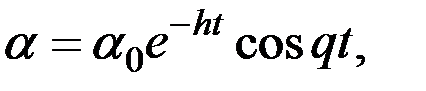(3.27)
где α₀ – начальное отклонение главной оси гироскопа относительно направления меридиана. Как следует из последнего равенства, в процессе установления в меридиан чувствительный элемент гирокомпаса совершает чисто гармонические колебания. Отсутствие экспоненциальной составляющей решения, имевшей место в двухгироскопных компасах, обусловлено тем, что постоянная времени акселерометра значительно меньше постоянной времени, определяющей скорость перетекания жидкости из сосуда в сосуд в гидравлическом успокоителе колебаний, и практически не влияет на характер переходного процесса.

Подводя итог сказанному отметим, что:

§

Важно!

процесс установления главной оси гироскопа в меридиан носит гармонический характер;

§ период затухающих колебаний чувствительного элемента зависит как от параметров прибора, так и от широты места судна и скорости его движения;

§ при отсутствии сигналов коррекции, сформированных внешними устройствами, после завершения переходного процесса гирокомпас будет иметь широтную и скоростную девиации;

введением сигналов внешней коррекции можно скомпенсировать систематические ошибки гирокомпаса.