Принцип действия гиротахометра

Принципиальная схема простейшего гиротахометра (ГТ), построенного на гироскопе с двумя степенями свободы, представлена на рис. 3.4. Ротор гироскопа установлен в кольце К карданового подвеса. Поворот кольца вокруг оси оу₀ ограничивается пружиной Пр, необходимой для создания восстанавливающего момента. Погашение собственных колебаний гироскопа осуществляется демпфером Д. Показания прибора, пропорциональные углу поворота кольца вокруг своей оси подвеса, снимаются в виде напряжения с потенциометра П. Оси ох₀у₀z₀ связаны с судном, а оси охуz, совмещенные в начальном положении (при β=0) с осями ох₀у₀z₀, - с рамкой прибора и в данном случае являются осями Резаля. Ось оz₀ является осью чувствительности или входной осью, так как гиротахометр реагирует, в основном, на поворот судна вокруг этой оси; ось оу называется выходной, ввиду того, что снимаемый с потенциометра П сигнал пропорционален углу поворота (прецессии) кольца К вокруг этой оси. Эту ось также называют осью прецессии.

Составим уравнения, описывающие работу гиротахометра. Результирующую угловую скорость вращения основания прибора будем представлять ее составляющими ω_х0, ω_у0 и ω_z0 по осям, связанным с судном. В общем случае к ротору гироскопа будут приложены следующие моменты (рис. 3.4):

§ момент М_г гироскопической реакции на внешние воздействия;

§ момент М_и сил инерции рамки и связанных с ней элементов, в частности ротора гироскопа;

§ момент М_д демпфирующих сил, порождаемых, в основном, демпфером Д;

§ момент М_пр упругих сил, порождаемый пружиной:

§ возмущающий момент (момент внешних сил) М_в.

В соответствие с принципом Даламбера сумма указанных моментов относительно оси оу должна быть равна нулю. Найдем выражения для указанных моментов.

Как известно, момент гироскопической реакции равен по модулю произведению кинетического момента гироскопа на составляющую абсолютной угловой скорости вращения его ротора вокруг оси oz:

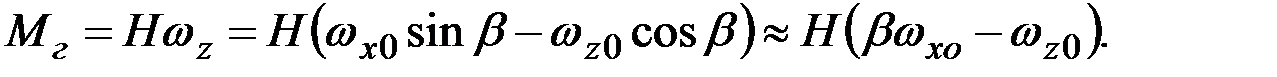(3.1)
Приближение, принятое в полученном выражении, допустимо вследствие малости значений угла β.

Момент сил инерции ротора и рамки подвеса будет определяться угловыми ускорениями 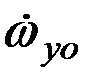вращения основания прибора и прецессии гироскопа:

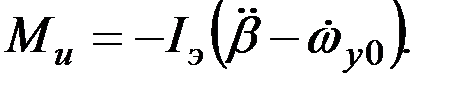(3.2)

Момент демпфирующих сил можно представить в следующем виде:

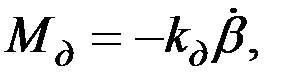(3.3)

где k_д – коэффициент демпфирования. Аналогично выглядит и выражение для момента упругих сил:

(3.4)
где с – коэффициент упругости, равный моменту, прикладываемому пружиной к рамке гироскопа, при единичном значении угла β.

Момент внешних сил определяется трением М_т в опорах подвеса рамки гироскопа, а также воздействиями f(t), возникающими из-за конструктивного и технологического несовершенства прибора:

(3.5)

Используя полученные выражения, уравнения, описывающие закон изменения угла поворота рамки подвеса, можно записать в виде:

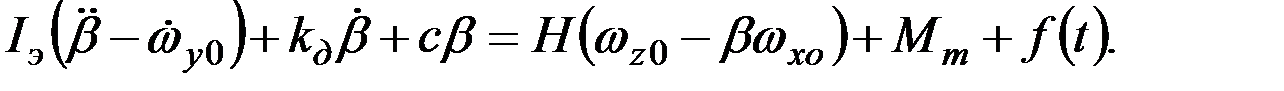(3.6)

Если основание прибора вращается в пространстве только с угловой скоростью ω_zo, а моменты сил трения в опорах подвеса и другие возмущающие моменты отсутствуют, то установившийся угол β_у отклонения главной оси от положения равновесия будет определяться следующим выражением:

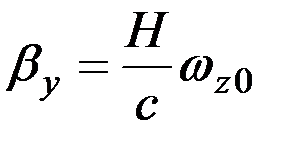. (3.7)

Полученное выражение показывает, что угол β, а, следовательно, и сигнал, снимаемый с потенциометра П (рис. 3.4), будут пропорциональны измеряемой угловой скорости ω_zo.

Однако факторы, опущенные в данном случае из рассмотрения, могут оказывать заметное влияние на точность показаний прибора. Так, влияние перекрестной составляющей ω_х0 угловой скорости вращения основания прибора увеличивается с увеличением угла β прецессии гироскопа. Поэтому на практике стремятся этот угол сделать по возможности минимальным или свести его вообще к нулю. Стремятся снизить также величину момента сил сухого трения или исключить его полностью. Для этого используют различного рода подвесы ротора гироскопа. В частности, широ

У

ДУ

Р

ДМ

Рис. 3.5

кое применение находят двухстепенные гироскопы, использующие гидростатический (поплавковый) или воздушный подвес чувствительного элемента. В этих моделях с целью повышения точности работы прибора механическая пружина заменяется “электрической” (рис. 3.5), представляющей собой сочетание датчика угла ДУ, формирующего напряжение, пропорциональное β, усилителя У и датчика момента ДМ. Последний прикладывает к рамке гироскопа момент, пропорциональный углу ее отклонения β. Сигнал об измеренной угловой скорости снимается с усилителя У.

Уравнения (3.6) можно представить и в ином виде [36]:

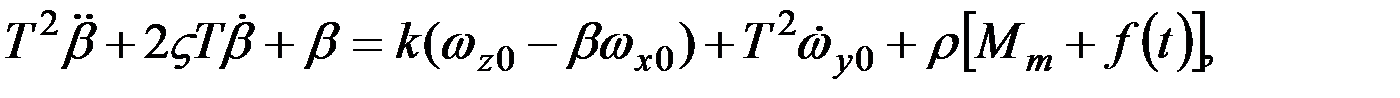(3.8)
где

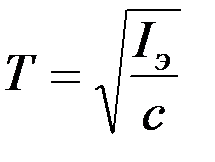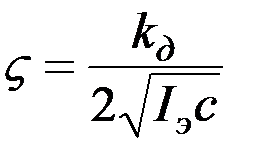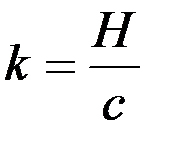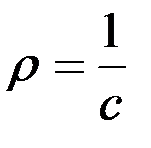, , , . (3.9)
Достоинством последней формы записи уравнений является то, что на их базе легко получить передаточные функции гиротахометра по отношению к рассматриваемым внешним воздействиям. Так, представляя уравнения в преобразованиях по Лапласу-Карсону [16], передаточную функцию по отношению к полезному воздействию можно записать в виде:

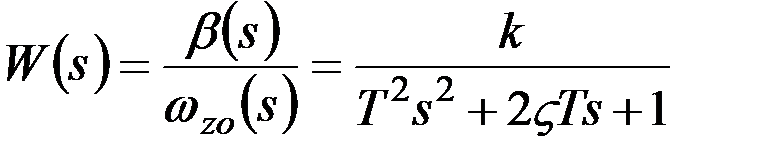. (3.10)

Как известно, выражение (3.10) позволяет не только оценить динамические характеристики исследуемого прибора, но широко используется при анализе работы различных систем автоматического управления, в которых применяются ГТ.