Лекция №4 Тема 2.1 Кинематика точки
Вопросы:
2.1.1.Введение в кинематику.
2.1.2. Основная задача кинематики.
2.1.3. Закон движения точки и способы его задания.
2.1.4. Скорость движения точки и способы её определения.
2.1.5. Ускорение движения точки и способы его определения.
Термин кинематика.Термин движение.
Для определения положения движущегося тела (или точки) в разные моменты времени с телом, по отношению к которому изучается движение, жестко связывают какую-нибудь систему координат, образующую вместе с этим телом систему отсчета. В дальнейшем будем говорить о движении тела (или точки) по отношению к данной системе отсчета, подразумевая под этим движение по отношению к тому телу, с которым эта система отсчета связана. Изображать систему отсчета будем в виде трех координатных осей.
Движение тел совершается в пространстве с течением времени. Пространство в механике мы рассматриваем как трехмерное евклидово пространство. Все измерения в нем производятся на основании методов евклидовой геометрии. За единицу длины при измерении расстояний принимается 1 м. Время в механике считается универсальным, т.е. протекающим одинаково во всех рассматриваемых системах отсчета. За единицу времени принимается 1 с. Размерность длины обозначается символом L, а времени – символом Т.
Евклидово пространство и универсальное время отражают реальные свойства пространства и времени лишь приближенно. Однако, как показывает опыт, для движений, которые изучаются в механике (движения со скоростями, далекими от скорости света), это приближение дает вполне достаточную для практики точность.
Время является скалярной, непрерывно изменяющейся величиной. В задачах кинематики время t принимают за независимую переменную (аргумент). Все другие переменные величины (расстояния, скорости и т, д.) рассматриваются как изменяющиеся с течением времени, т.е. как функции времени t. Отсчет времени ведется от некоторого начального момента (t=0), о выборе которого в каждом случае условливаются. Всякий данный момент времени t определяется числом секунд, прошедших от начального момента до данного; разность между какими-нибудь двумя последовательными моментами времени называется промежутком времени.
Для решения задач кинематики надо, чтобы изучаемое движение было как-то задано (описано).
Кинематически задать движение или закон движения тела (точки) – значит задать положение этого тела (точки) относительно данной системы отсчета в любой момент времени. Установление математических способов задания движения точек или тел является одной из важных задач кинематики. Поэтому изучение движения любого объекта будем начинать с установления способов задания этого движения.
Термин траектория точки
Способы задания движения точки
Для задания движения точки можно применять одни из следующих трех способов: векторный, координатный или естественный.
1) Векторный способ задания движения точки
Пусть точка М движется по отношению к некоторой системе отсчета Охуz. Положение этой точки в любой момент времени можно определить, задав ее радиус-вектор 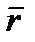 , проведенный из начала координат О в точку М (рисунок 2_1).
, проведенный из начала координат О в точку М (рисунок 2_1).
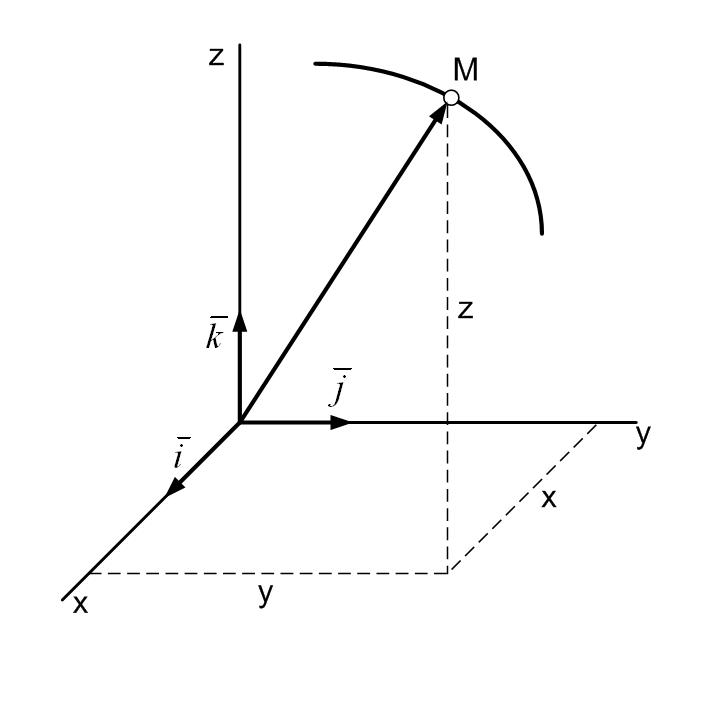
При движении точки М вектор 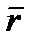 будет с течением времени изменяться и по модулю, и по направлению. Следовательно,
будет с течением времени изменяться и по модулю, и по направлению. Следовательно, 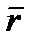 является переменным вектором (вектором-функцией), зависящим от аргумента t:
является переменным вектором (вектором-функцией), зависящим от аргумента t:
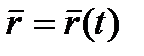
| (2.1) |
Равенство (2.1) и определяет закон движения точки в векторной форме, так как оно позволяет в любой момент времени построить соответствующий вектор 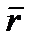 и найти положение движущейся точки.
и найти положение движущейся точки.
Геометрическое место концов вектора 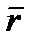 , т. е. годограф этого вектора, определяет траекторию движущейся точки.
, т. е. годограф этого вектора, определяет траекторию движущейся точки.
Аналитически, как известно, вектор задается его проекциями на координатные оси. В прямоугольных декартовых координатах для вектора 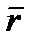 будет:
будет: 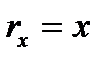 ,
, 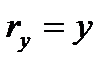 ,
, 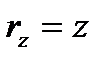 (рисунок 2_1), где х, у, z – декартовы координаты точки. Тогда, если ввести единичные векторы (орты)
(рисунок 2_1), где х, у, z – декартовы координаты точки. Тогда, если ввести единичные векторы (орты) 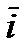 ,
, 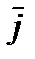 ,
, 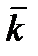 координатных осей, получим для
координатных осей, получим для 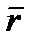 выражение
выражение
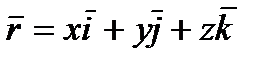
| (2.2) |
Следовательно, зависимость (2.1) 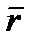 от t будет известна, если будут заданы координаты х, у, z точки как функции времени. Такой способ задания движения точки (координатный) рассмотрим ниже. Вектор
от t будет известна, если будут заданы координаты х, у, z точки как функции времени. Такой способ задания движения точки (координатный) рассмотрим ниже. Вектор 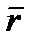 может быть задан, как известно, и иными способами, например его модулем и углами с осями или проекциями на оси других систем координат. Для получения общих формул, не зависящих от того, как конкретно задан вектор
может быть задан, как известно, и иными способами, например его модулем и углами с осями или проекциями на оси других систем координат. Для получения общих формул, не зависящих от того, как конкретно задан вектор 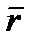 , будем исходить из векторного закона движения, представленного равенством (2.1).
, будем исходить из векторного закона движения, представленного равенством (2.1).
2) Координатный способ задания движения точки
Положение точки можно непосредственно определять ее декартовыми координатами х, у, z, которые при движении точки будут с течением времени изменяться. Чтобы знать закон движения точки, т. е. ее положение в пространстве в любой момент времени, надо знать значения координат точки для каждого момента времени, т. е. знать зависимости
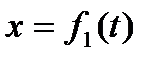 , , 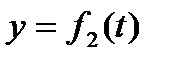 , , 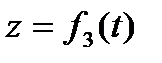 . .
| (2.3) |
Уравнения (2.3) представляют собой уравнения движения точки в прямоугольных декартовых координатах. Они определяют закон движения точки при координатном способе задания движения.
Если движение точки происходит все время в одной и той же плоскости, то, приняв эту плоскость за плоскость Оху, получим в этом случае два уравнения движения:
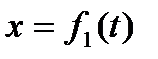 , , 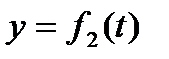 . .
| (2.4) |
Наконец, при прямолинейном движении точки, если вдоль ее траектории направить координатную ось Ох, движение будет определяться одним уравнением (законом прямолинейного движения точки)
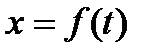
| (2.5) |
Уравнения (2.3) и (2.4) представляют собой одновременно уравнения траектории точки в параметрической форме, где роль параметра играет время t. Исключив из уравнений движения время t, можно найти уравнение траектории в обычной форме, т. е. в виде, дающем зависимость между координатами точки.
3) Естественный способ задания движения точки.
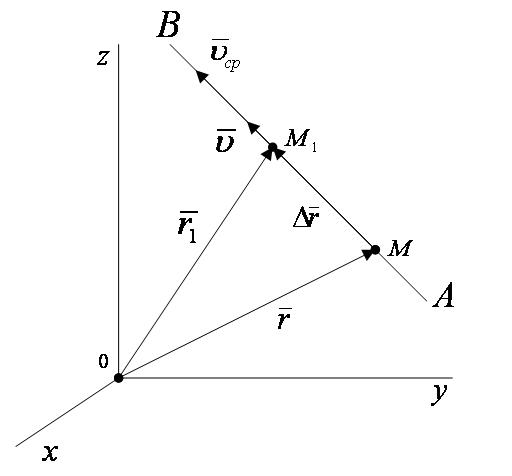
Естественным (или траекторным) способом задания движения удобно пользоваться в тех случаях, когда траектория движущейся точки известна заранее. Пусть кривая АВ является траекторией точки М при ее движении относительно системы отсчета Oxyz (рисунок 2_2).
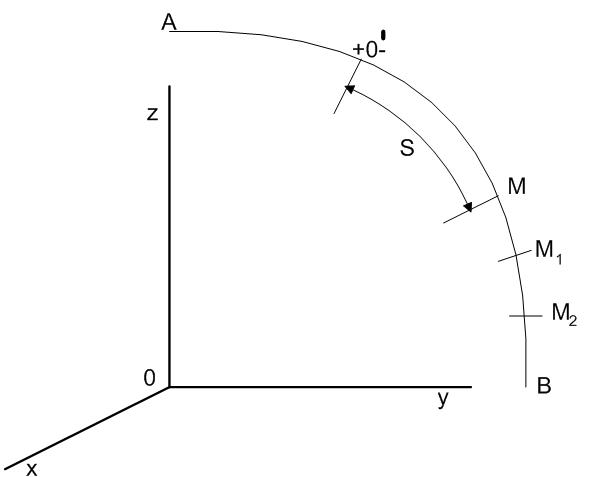
Выберем на этой траектории какую-нибудь неподвижную точку О', которую примем за начало отсчета, и установим на траектории положительное и отрицательное направления отсчета (как на координатной оси). Тогда положение точки М на траектории будет однозначно определяться криволинейной координатой s, которая равна расстоянию от точки О' до точки М, измеренному вдоль дуги траектории и взятому с соответствующим знаком. При движении точка М перемещается в положения 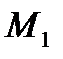 ,
, 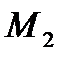 , …, следовательно, расстояние будет с течением времени изменяться. Чтобы знать положение точки М на траектории в любой момент времени, надо знать зависимость
, …, следовательно, расстояние будет с течением времени изменяться. Чтобы знать положение точки М на траектории в любой момент времени, надо знать зависимость
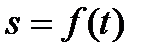
| (2.6) |
Уравнение (2.6) и выражает закон движения точки М вдоль траектории.
Таким образом, чтобы задать движение точки естественным способом, надо задать: 1) траекторию точки; 2) начало отсчета на траектории с указанием положительного и отрицательного направлений отсчета; 3) закон движения точки вдоль траектории в виде 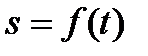 .
.
Вектор скорости точки
Одной из основных кинематических характеристик движения точки является векторная величина, называемая скоростью точки. Введем сначала понятие о средней скорости точки за какой-нибудь промежуток времени. Пусть движущаяся точка находится в момент времени t в положении М, определяемом радиусом-вектором 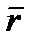 , а в момент
, а в момент 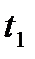 приходит в положение
приходит в положение 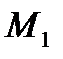 , определяемое вектором
, определяемое вектором 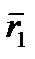 (рисунок 2_3).
(рисунок 2_3).
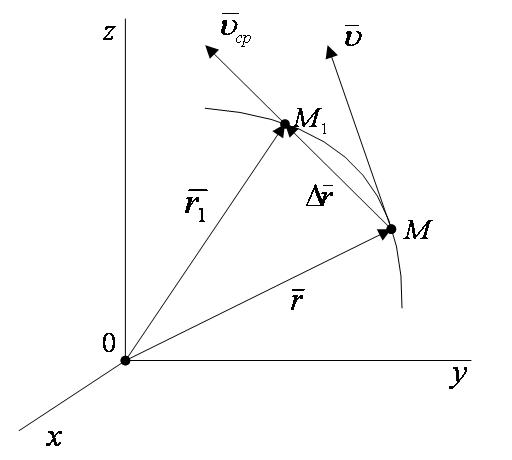
Тогда перемещение точки за промежуток времени 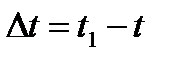 определяется вектором
определяется вектором 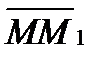 ,который будем называть вектором перемещения точки. Этот вектор направлен по хорде, если точка движется, криволинейно (рисунок 2_3), и вдоль самой траектории АВ, когда движение является прямолинейным (рисунок 2_4).
,который будем называть вектором перемещения точки. Этот вектор направлен по хорде, если точка движется, криволинейно (рисунок 2_3), и вдоль самой траектории АВ, когда движение является прямолинейным (рисунок 2_4).
Из треугольника 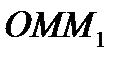 видно, что
видно, что 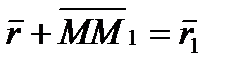 ; следовательно,
; следовательно, 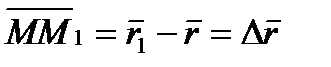 . Таким образом средняя скорость за промежуток времени
. Таким образом средняя скорость за промежуток времени 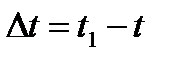 определяется по формуле:
определяется по формуле:
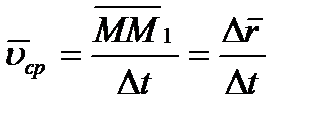
| (2.7) |
Направлен вектор 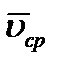 так же, как и вектор
так же, как и вектор 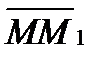 , т. е. при криволинейном движении вдоль хорды
, т. е. при криволинейном движении вдоль хорды 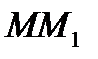 в сторону движения точки, а при прямолинейном движении – вдоль самой траектории (от деления на
в сторону движения точки, а при прямолинейном движении – вдоль самой траектории (от деления на 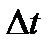 направление вектора не изменяется).
направление вектора не изменяется).
Очевидно, что чем меньше будет промежуток времени 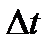 , для которого вычислена средняя скорость, тем величина
, для которого вычислена средняя скорость, тем величина 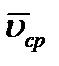 будет точнее характеризовать движение точки. Чтобы получить точную характеристику движения, вводят понятие о скорости точки в данный момент времени, которую определяет векторная величина
будет точнее характеризовать движение точки. Чтобы получить точную характеристику движения, вводят понятие о скорости точки в данный момент времени, которую определяет векторная величина 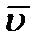 , к которой стремится средняя скорость
, к которой стремится средняя скорость 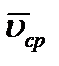 при стремлении промежутка времени
при стремлении промежутка времени 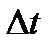 к нулю. Согласно определения:
к нулю. Согласно определения: 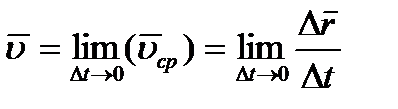 . Предел отношения
. Предел отношения 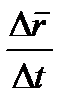 при
при 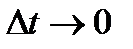 представляет собой первую производную от вектора
представляет собой первую производную от вектора 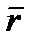 по аргументу t и обозначается, как и производная от скалярной функции, символом
по аргументу t и обозначается, как и производная от скалярной функции, символом 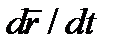 . Окончательно получаем
. Окончательно получаем
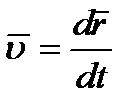
| (2.8) |
Итак, вектор скорости точки в данный момент времени равен первой производной от радиуса-вектора точки по времени.
Так как предельным направлением секущей 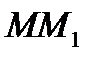 является касательная, то вектор скорости точки в данный момент времени направлен по касательной к траектории точки в сторону движения.
является касательная, то вектор скорости точки в данный момент времени направлен по касательной к траектории точки в сторону движения.
Формула (1.8) показывает также, что вектор скорости 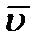 равен отношению элементарного перемещения точки
равен отношению элементарного перемещения точки 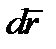 , направленного по касательной к траектории, к соответствующему промежутку времени
, направленного по касательной к траектории, к соответствующему промежутку времени 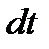 .
.
При прямолинейном движении вектор скорости 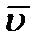 все время направлен вдоль прямой, по которой движется точка, и может изменяться лишь численно; при криволинейном движении кроме числового значения все время изменяется и направление вектора скорости точки. Размерность скорости L/T, т. е. длина/время; в качестве единиц измерения применяют обычно м/с или км/ч.
все время направлен вдоль прямой, по которой движется точка, и может изменяться лишь численно; при криволинейном движении кроме числового значения все время изменяется и направление вектора скорости точки. Размерность скорости L/T, т. е. длина/время; в качестве единиц измерения применяют обычно м/с или км/ч.
Вектор ускорения точки
Термин ускорение.
Пусть в некоторый момент времени t движущаяся точка находится в положении М и имеет скорость 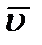 , а в момент
, а в момент 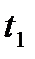 приходит в положение
приходит в положение 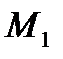 и имеет скорость
и имеет скорость 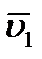 (рисунок 2_5).
(рисунок 2_5).
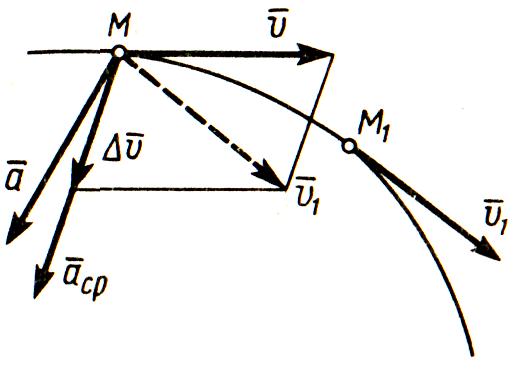
Тогда за промежуток времени 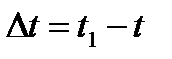 скорость точки получает приращение
скорость точки получает приращение 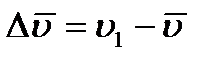 . Для построения вектора
. Для построения вектора 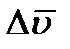 отложим от точки М вектор, равный
отложим от точки М вектор, равный 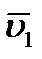 и построим параллелограмм, в котором диагональю будет
и построим параллелограмм, в котором диагональю будет 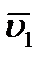 , a одной из сторон
, a одной из сторон 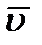 . Тогда, очевидно, вторая сторона и будет изображать вектор
. Тогда, очевидно, вторая сторона и будет изображать вектор 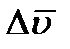 . Заметим, что вектор
. Заметим, что вектор 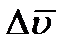 всегда направлен в сторону вогнутости траектории.
всегда направлен в сторону вогнутости траектории.
Отношение приращения вектора скорости 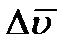 к соответствующему промежутку времени
к соответствующему промежутку времени 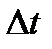 определяет вектор среднего ускорения точки за этот промежуток времени:
определяет вектор среднего ускорения точки за этот промежуток времени:
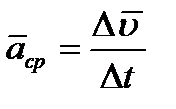
| (2.9) |
Вектор среднего ускорения имеет то же направление, что и вектор 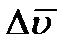 , т. е. направлен в сторону вогнутости траектории.
, т. е. направлен в сторону вогнутости траектории.
Ускорение точки в данный момент времени t характеризует векторная величина 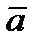 , к которой стремится среднее ускорение
, к которой стремится среднее ускорение 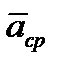 при стремлении промежутка времени
при стремлении промежутка времени 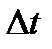 к нулю:
к нулю: 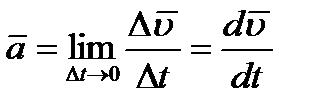 или, с учетом равенства (2.8),
или, с учетом равенства (2.8),
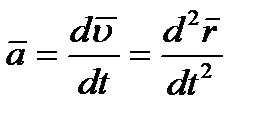
| (2.10) |
Следовательно, вектор ускорения точки в данный момент времени равен первой производной от вектора скорости или второй производной от радиуса-вектора точки по времени.
Размерность ускорения L/T2, т.е. длина/(время)2; в качестве единицы измерения применяется обычно м/с2.
Из формулы (2.10) следует также, что вектор ускорения точки 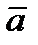 равен отношению элементарного приращения вектора скорости
равен отношению элементарного приращения вектора скорости 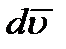 к соответствующему промежутку времени
к соответствующему промежутку времени 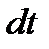 .
.
Найдем, как располагается вектор а по отношению к траектории точки. При прямолинейном движении вектор 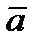 направлен вдоль прямой, по которой движется точка. Если траекторией точки является плоская кривая, то вектор ускорения
направлен вдоль прямой, по которой движется точка. Если траекторией точки является плоская кривая, то вектор ускорения 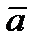 , так же как и вектор
, так же как и вектор 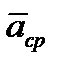 , лежит в плоскости этой кривой и направлен в сторону ее вогнутости. Если траектория не является плоской кривой, то вектор
, лежит в плоскости этой кривой и направлен в сторону ее вогнутости. Если траектория не является плоской кривой, то вектор 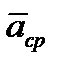 направлен в сторону вогнутости траектории и лежит в плоскости, проходящей через касательную к траектории в точке М и прямую, параллельную касательной в соседней точке
направлен в сторону вогнутости траектории и лежит в плоскости, проходящей через касательную к траектории в точке М и прямую, параллельную касательной в соседней точке 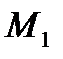 (рисунок 2_5).
(рисунок 2_5).

В пределе, когда точка 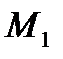 стремится к М, эта плоскость занимает положение так называемой соприкасающейся плоскости, т. е. плоскости, в которой происходит бесконечно малый поворот касательной к траектории при элементарном перемещении движущейся точки. Следовательно, в общем случае вектор ускорения
стремится к М, эта плоскость занимает положение так называемой соприкасающейся плоскости, т. е. плоскости, в которой происходит бесконечно малый поворот касательной к траектории при элементарном перемещении движущейся точки. Следовательно, в общем случае вектор ускорения 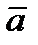 лежит в соприкасающейся плоскости и направлен в сторону вогнутости кривой.
лежит в соприкасающейся плоскости и направлен в сторону вогнутости кривой.
Определение скорости и ускорения точки при координатном способе задания движения
Найдем, как вычисляются скорость и ускорение точки, если ее движение задано уравнениями (2.3) или (2.4).
Формулы (2.8) и (2.10), определяющие значения 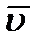 и
и 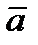 , содержат производные по времени от векторов
, содержат производные по времени от векторов 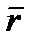 и
и 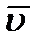 . В равенствах, содержащих производные от векторов, переход к зависимостям между их проекциями осуществляется с помощью следующей теоремы: проекция производной от вектора на ось, неподвижную в данной системе отсчета, равна производной от проекции дифференцируемого вектора на ту же ось, т. е.,
. В равенствах, содержащих производные от векторов, переход к зависимостям между их проекциями осуществляется с помощью следующей теоремы: проекция производной от вектора на ось, неподвижную в данной системе отсчета, равна производной от проекции дифференцируемого вектора на ту же ось, т. е.,
если 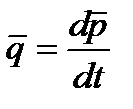 , то , то 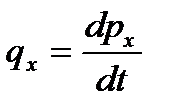 , , 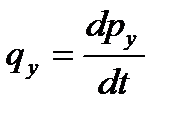 , , 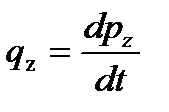 . .
| (2.11) |
Вектор скорости точки 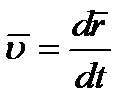 . Отсюда на основании формул (2.11), учитывая, что
. Отсюда на основании формул (2.11), учитывая, что 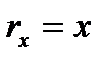 ,
, 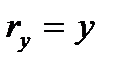 ,
, 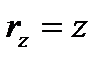 , найдем:
, найдем:
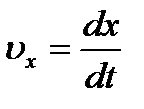 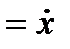 , , 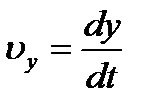 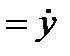 , , 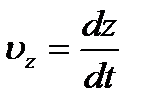 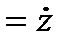 . .
| (2.12) |
где точка над буквой есть символ дифференцирования по времени. Таким образом, проекции скорости точки на координатные оси равны первым производным от соответствующих координат точки по времени.
Зная проекции скорости, найдем ее модуль и направление (т. е. углы α, β, γ, которые вектор 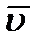 образует с координатными осями) по формулам
образует с координатными осями) по формулам
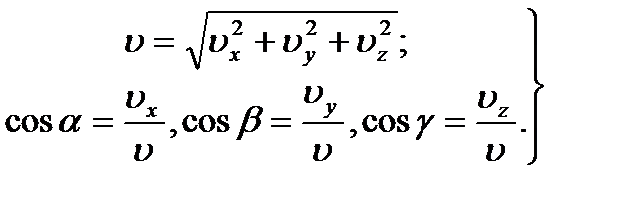
| (2.13) |
Вектор ускорения точки 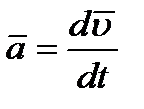 . Отсюда на основании формул (2.11) получаем:
. Отсюда на основании формул (2.11) получаем:
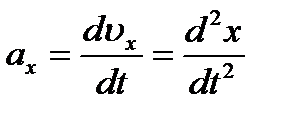 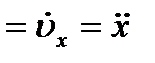 , , 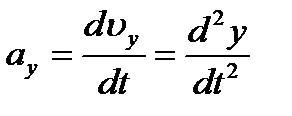 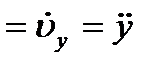 , , 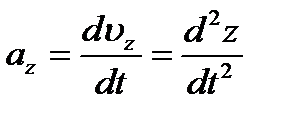 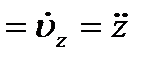
| (2.14) |
т. е. проекции ускорения точки на координатные оси равны первым производным от проекций скорости или вторым производным от соответствующих координат точки по времени. Модуль и направление ускорения найдутся из формул
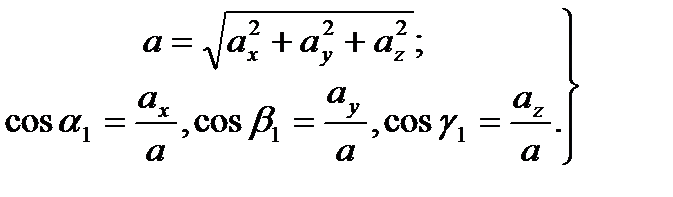
| (2.15) |
где 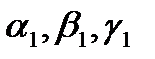 – углы, образуемые вектором ускорения с координатными осями.
– углы, образуемые вектором ускорения с координатными осями.
Итак, если движение точки задано в декартовых прямоугольных координатах уравнениями (2.3) или (2.4), то скорость точки определяется по формулам (2.12) и (2.13), а ускорение – по формулам (2.14) и (2.15). При этом в случае движения, происходящего в одной плоскости, во всех формулах должна быть отброшена проекция на ось z.
В случае же прямолинейного движения, которое задается одним уравнением 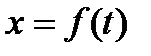 , будет
, будет
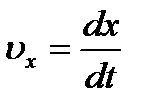 , , 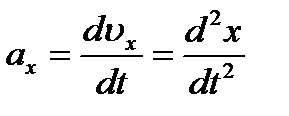
| (2_16) |
Равенства (2.16) и определяют значения скорости и ускорения точки в этом случае.
2.1.6 Оси естественного трехгранника. Числовое значение скорости
Рассмотрим, как вычисляются скорость и ускорение точки при естественном способе задания движения, т.е. когда заданы траектория точки и закон движения точки вдоль этой траектории в виде 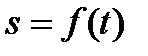 .
.
В этом случае значения векторов 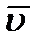 и
и 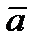 определяют по их проекциям не на оси системы отсчета Oxyz, а на подвижные оси
определяют по их проекциям не на оси системы отсчета Oxyz, а на подвижные оси 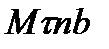 , имеющие начало в точке М и движущиеся вместе с нею (рисунок 2_6).
, имеющие начало в точке М и движущиеся вместе с нею (рисунок 2_6).
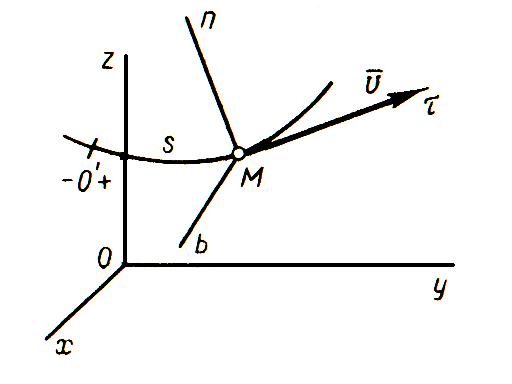
Эти оси, называемые осями естественного трехгранника (или скоростными осями), направлены следующим образом: ось 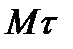 – по касательной к траектории в сторону положительного отсчета расстояния s; ось
– по касательной к траектории в сторону положительного отсчета расстояния s; ось 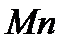 – по нормали к траектории, лежащей в соприкасающейся плоскости и направленной в сторону вогнутости траектории; ось
– по нормали к траектории, лежащей в соприкасающейся плоскости и направленной в сторону вогнутости траектории; ось 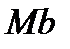 – перпендикулярно к первым двум так, чтобы она образовала с ними правую систему осей. Нормаль
– перпендикулярно к первым двум так, чтобы она образовала с ними правую систему осей. Нормаль 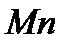 , лежащая в соприкасающейся плоскости (в плоскости самой кривой, если кривая плоская), называется главной нормалью, а перпендикулярная ей нормаль
, лежащая в соприкасающейся плоскости (в плоскости самой кривой, если кривая плоская), называется главной нормалью, а перпендикулярная ей нормаль 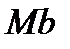 – бинормалью.
– бинормалью.
Скорость точки, направленная по касательной к траектории (рисунок 2_6),

определяется в осях 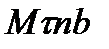 только одной проекцией
только одной проекцией 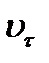 на ось
на ось 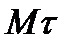 . При этом
. При этом 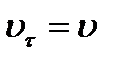 или
или 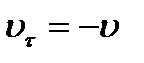 . Следовательно,
. Следовательно, 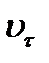 или совпадает с модулем скорости
или совпадает с модулем скорости 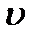 , или отличается от
, или отличается от 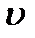 только знаком. Условимся поэтому в дальнейшем обозначать
только знаком. Условимся поэтому в дальнейшем обозначать 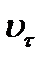 тоже символом
тоже символом 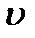 , опуская индекс
, опуская индекс 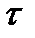 , и называть
, и называть 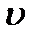 числовым (или алгебраическим) значением скорости. Модуль скорости во всех случаях, когда это не может вызвать недоразумений, будем тоже обозначать символом
числовым (или алгебраическим) значением скорости. Модуль скорости во всех случаях, когда это не может вызвать недоразумений, будем тоже обозначать символом 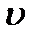 , а когда надо подчеркнуть, что речь идет о модуле скорости, – применять символ
, а когда надо подчеркнуть, что речь идет о модуле скорости, – применять символ 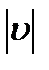 .
.
Найдем значение 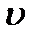 . Если за промежуток времени
. Если за промежуток времени 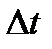 точка совершит вдоль дуги траектории перемещение
точка совершит вдоль дуги траектории перемещение 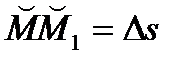 , где одновременно
, где одновременно 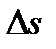 – приращение координаты s, то численно средней скоростью точки за этот промежуток времени будет
– приращение координаты s, то численно средней скоростью точки за этот промежуток времени будет 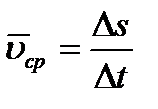 и в пределе найдем, что
и в пределе найдем, что
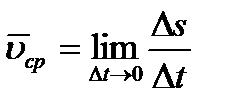 или или 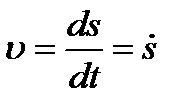
| (2.17) |
Таким образом, числовое значение скорости точки в данный момент времени равно первой производной от расстояния (криволинейной координаты) s этой точки по времени.
Значение 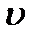 можно также находить как отношение элементарного перемещения ds точки к соответствующему промежутку времени dt. Так как всегда
можно также находить как отношение элементарного перемещения ds точки к соответствующему промежутку времени dt. Так как всегда 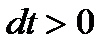 , то знак
, то знак 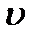 совпадает со знаком ds. Следовательно, когда
совпадает со знаком ds. Следовательно, когда 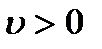 , скорость направлена в сторону положительного отсчета расстояния s, а когда
, скорость направлена в сторону положительного отсчета расстояния s, а когда 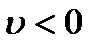 , – в противоположную, сторону. Таким образом, величина
, – в противоположную, сторону. Таким образом, величина 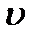 одновременно определяет и модуль скорости, и сторону, куда она направлена.
одновременно определяет и модуль скорости, и сторону, куда она направлена.
Касательное и нормальное ускорения точки
Ранее было установлено, что ускорение 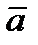 точки лежит в соприкасающейся плоскости, т. е. в плоскости
точки лежит в соприкасающейся плоскости, т. е. в плоскости 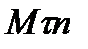 . Следовательно, проекция вектора
. Следовательно, проекция вектора 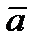 на бинормаль
на бинормаль 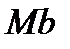 равна нулю
равна нулю 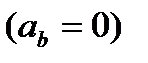 . Найдем проекции
. Найдем проекции 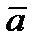 на две другие оси. Проектируя обе части равенства (2.10) на оси
на две другие оси. Проектируя обе части равенства (2.10) на оси 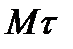 и
и 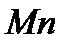 и обозначая символами
и обозначая символами 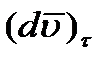 и
и 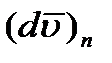 проекции вектора
проекции вектора 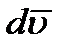 на эти оси, получим:
на эти оси, получим:
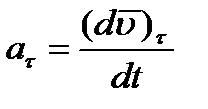 , , 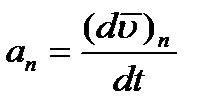
| (2.18) |
Вектор 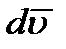 представляет собой разность между скоростями в двух соседних точках М и М' (рисунок 2_7),
представляет собой разность между скоростями в двух соседних точках М и М' (рисунок 2_7),
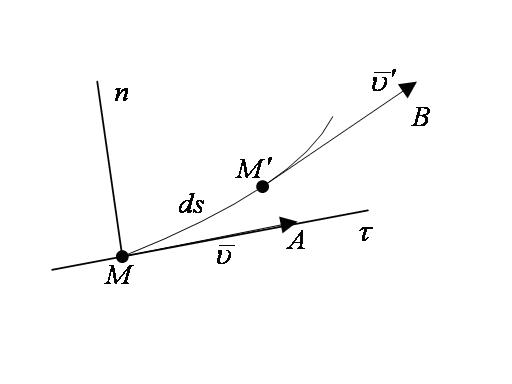
т. е. 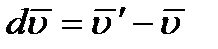 . Отложим векторы
. Отложим векторы 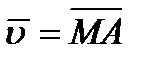 и
и 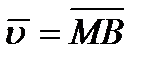 от общего начала (рисунок 2_8);
от общего начала (рисунок 2_8);
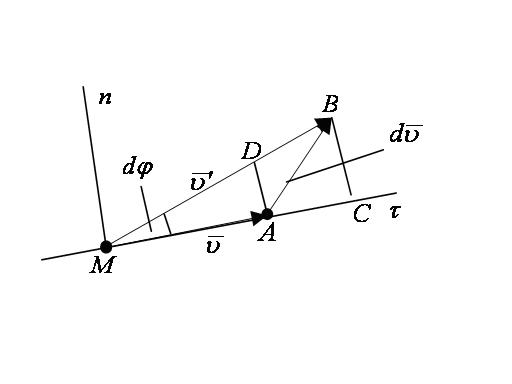
тогда 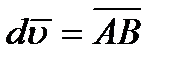 , а фигуру ACBD при бесконечно малом угле
, а фигуру ACBD при бесконечно малом угле 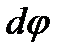 можно рассматривать как прямоугольник.
можно рассматривать как прямоугольник.
Отсюда 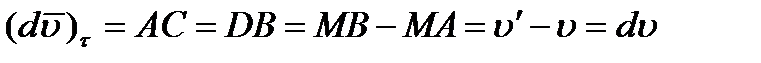 , где
, где 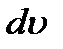 – элементарное приращение числового значения скорости. Далее, поскольку предел отношения дуги к хорде равен единице, можно AD рассматривать как элементарную дугу радиуса МА, размер которой определяется произведением радиуса на центральный угол. Тогда
– элементарное приращение числового значения скорости. Далее, поскольку предел отношения дуги к хорде равен единице, можно AD рассматривать как элементарную дугу радиуса МА, размер которой определяется произведением радиуса на центральный угол. Тогда 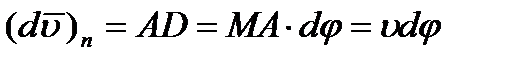 .
.
Подставляя найденные значения 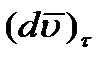 и
и 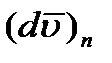 в равенства (2.18), получим:
в равенства (2.18), получим:
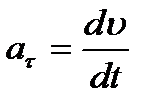 , , 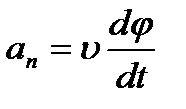
| (2.19) |
Термин угол смежности (4). Тогда dφ – элементарный угол смежности. Напомним, что отношение dφ к ds , равное 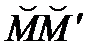 , определяет кривизну кривой в точке М, а кривизна k является величиной, обратной радиусу кривизны ρ в этой точке, т. е.
, определяет кривизну кривой в точке М, а кривизна k является величиной, обратной радиусу кривизны ρ в этой точке, т. е.
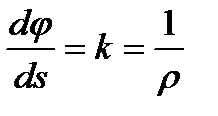
| (2.20) |
Введем эту величину во второе из равенств (2.19) и преобразуем его, учтя еще равенство (2.17), к виду 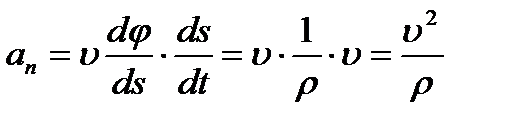 .
.
В результате окончательно получим:
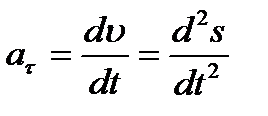 , , 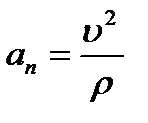 , , 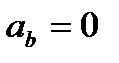
| (2.21) |
Таким образом, мы доказали, что проекция ускорения точки на касательную равна первой производной от числового значения скорости или второй производной от расстояния (криволинейной координаты) s по времени, а проекция ускорения на главную нормаль равна квадрату скорости, деленному на радиус кривизны траектории в данной точке кривой; проекция ускорения на бинормаль равна нулю. Это одна из важных теорем кинематики. Величины 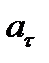 и
и 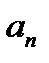 называют касательным и нормальным ускорениями точки.
называют касательным и нормальным ускорениями точки.
При движении точки М в одной плоскости касательная 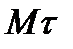 поворачивается вокруг бинормали
поворачивается вокруг бинормали 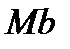 с угловой скоростью
с угловой скоростью 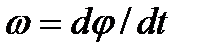 .
.
Отложим вдоль касательной 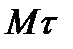 и главной нормали
и главной нормали 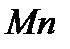 векторы
векторы 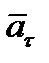 и
и 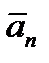 , т. е. касательную и нормальную составляющие ускорения (рисунок 2_9).
, т. е. касательную и нормальную составляющие ускорения (рисунок 2_9).
При этом составляющая 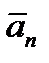 будет всегда направлена в сторону вогнутости кривой, так как всегда
будет всегда направлена в сторону вогнутости кривой, так как всегда 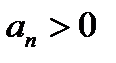 , а составляющая
, а составляющая 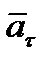 может быть направлена или в положительном, или в отрицательном направлении оси
может быть направлена или в положительном, или в отрицательном направлении оси 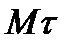 в зависимости от знака проекции
в зависимости от знака проекции 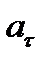 (рисунки 2_9, 2_10).
(рисунки 2_9, 2_10).

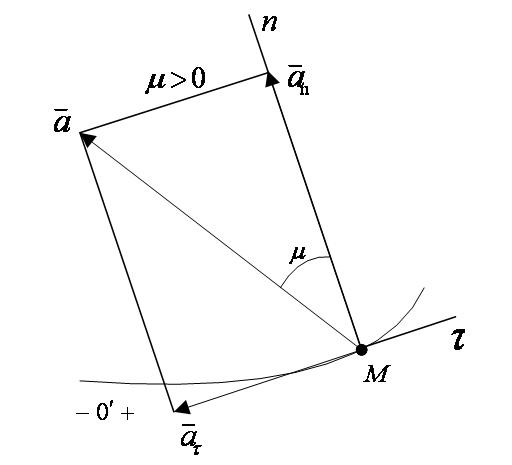
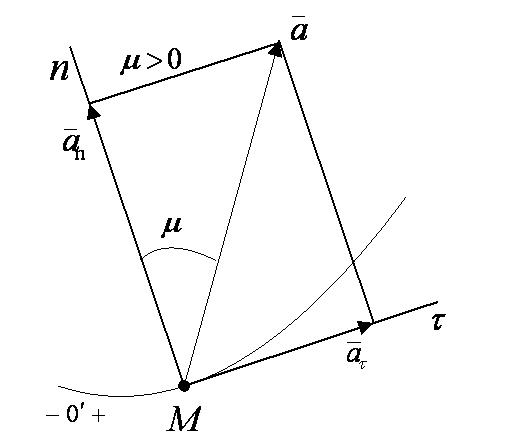
Вектор ускорения точки 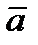 изображается диагональю параллелограмма, построенного на составляющих
изображается диагональю параллелограмма, построенного на составляющих 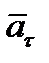 и
и 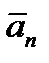 . Так как эти составляющие взаимно перпендикулярны, то модуль вектора
. Так как эти составляющие взаимно перпендикулярны, то модуль вектора 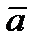 и угол μ его отклонения от нормали
и угол μ его отклонения от нормали 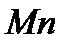 определятся формулами:
определятся формулами:
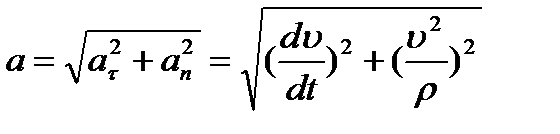 , , 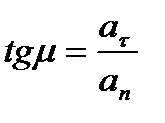
| (2.22) |
где 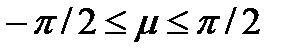 ; при
; при 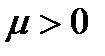 вектор
вектор 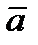 отклонен от нормали
отклонен от нормали 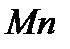 в сторону оси
в сторону оси 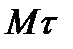 , а при
, а при 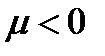 – в противоположную сторону (рисунок 2_10).
– в противоположную сторону (рисунок 2_10).

Таким образом, если движение точки задано естественным способом, то, зная траекторию (а следовательно, и ее радиус кривизны ρ в любой точке) и закон движения, т. е. зависимость 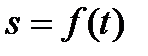 , можно по формулам (2.17) и (2.21), (2.22) определить модуль и направление векторов скор
, можно по формулам (2.17) и (2.21), (2.22) определить модуль и направление векторов скор
Дата добавления: 2021-06-28; просмотров: 591;











