II. Формализация процесса формирования математических моделей
Существующие методы формализации процесса формирования математических моделей электрических цепей широко используют понятия теории графов [27]. Здесь будет применен подход, в котором нет необходимости предварительного изучения теории графов. Для простоты ограничимся формированием математических моделей цепей состоящих из двухполюсных элементов, представленных на рис 2.
В качестве примера для формирования модели выберем цепь, представленную на рис. 3 (а). Соотношения на индуктивных элементах:
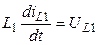 ;
; 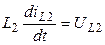 .
.
На емкостных элементах:
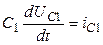 ;
; 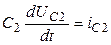 .
.
Закон Ома на резистивных элементах:
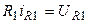 ;
; 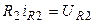 .
.
| Символ элемента | Тип элемента | Характеризующий его параметр |

| Резистор | R |
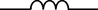
| Индуктивность | L |

| Емкость | C |

| Источник напряжения | U |
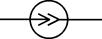
| Источник тока | I |
Рис. 2
I закон Кирхгофа выпишем для узлов 2, 3, 4, 5; причем условимся за положительное направление тока через элементы выбирать направление от узла с меньшим номером к узлу с большим номером.
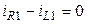 ;
; 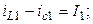
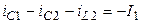 ;
; 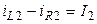 .
.
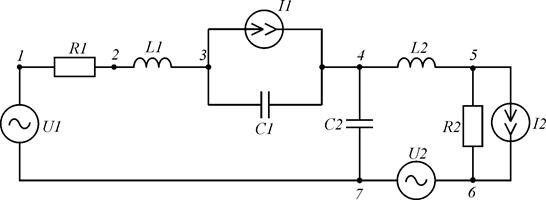
а)
| 2 | 4 | 3 | 4 | 1 | 5 | 3 | 5 | 1 | 7 |
| L1 | L2 | C1 | C2 | R1 | R2 | I1 | I2 | U1 | U2 |
| 3 | 5 | 4 | 7 | 2 | 6 | 4 | 6 | 7 | 6 |
б)
| 2 | 4 | 4 | 4 | 1 | 6 | 6 | 7 | 7 | 7 |
| L1 | L2 | C1 | I1 | R1 | R2 | I2 | C2 | U1 | U2 |
| 3 | 5 | 3 | 3 | 2 | 5 | 5 | 4 | 1 | 6 |
в)
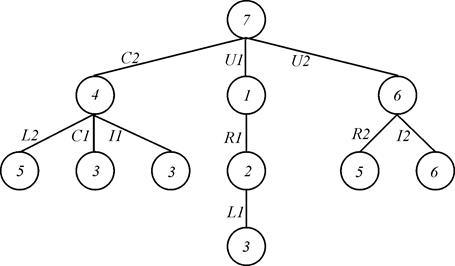
г)
3 – L1 – 2 – R1 – 1 – U1 – 7 – C2 – 4 – C1 – 3
5 – L2 – 4 – C2 – 7 – U2 – 6 – R2 – 5
д)
Рис. 3
Выберем контуры
1 – R1 – 2 – L1 – 3 – C1 – 4 – C2 – 7 – U1 – 1
4 – L2 – 5 – R2 – 6 – U2 – 7 – C2 – 4
и выпишем для них II закон Кирхгофа:
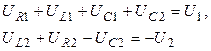
Из уравнений для токов и закона Ома находим
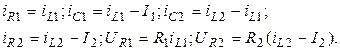
Используя соотношения, полученные на основании II закона Киргофа, найдем
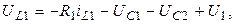
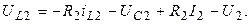
Окончательно математическая модель имеет вид
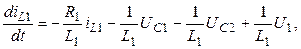 (1)
(1)
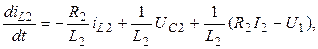
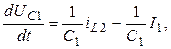
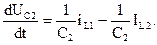
Компактно эту модель можно представить в матрично-векторной записи
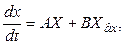 (2)
(2)
где
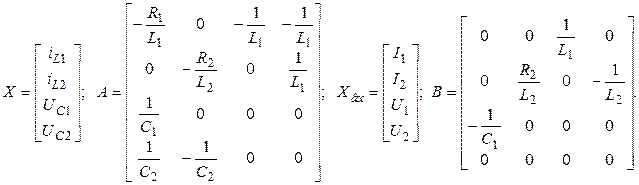
В общем случае математическую модель при заданной топологии цепи (фиксированная структура) представляется в виде системы матрично-векторных уравнений.
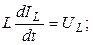 (3)
(3)
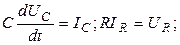
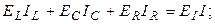
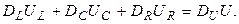
Здесь 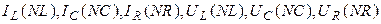 - вектора токов и напряжений на соответствующих элементах; NL, NC, NR – число индуктивных, емкостных и резистивных элементов, определяющих размерность векторов; L(NL, NL), C(NC, NC), R(NR, NR) – диагональные матрицы из индуктивностей, емкостей и сопротивлений; I(NI), U(NU) – вектора входных токов и напряжений; NI, NU – число источников тока и напряжения;
- вектора токов и напряжений на соответствующих элементах; NL, NC, NR – число индуктивных, емкостных и резистивных элементов, определяющих размерность векторов; L(NL, NL), C(NC, NC), R(NR, NR) – диагональные матрицы из индуктивностей, емкостей и сопротивлений; I(NI), U(NU) – вектора входных токов и напряжений; NI, NU – число источников тока и напряжения; 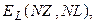
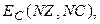
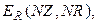
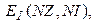
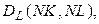
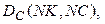
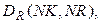
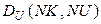 - топологические матрицы; NZ – число узлов, для которых записывается I закон Кирхгофа; NK- число контуров, для которых записывается II закон Кирхгофа.
- топологические матрицы; NZ – число узлов, для которых записывается I закон Кирхгофа; NK- число контуров, для которых записывается II закон Кирхгофа.
Для рассмотренного примера
NL, NC, NR, NI, NU=2, NZ=4, NK=2.
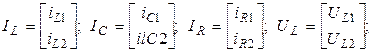
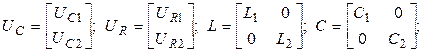
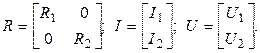
Задача формирования модели состоит, во-первых, в нахождении элементов топологических матриц и, во-вторых, в преобразовании модели к некоторому удобному для реализации виду.
Преобразуем модель (3) к виду (2), где
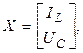
а матрицы A и B следует найти.
Обозначим
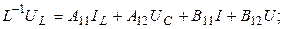
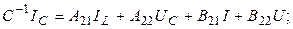
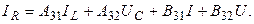
Размерность введенных матриц и векторов
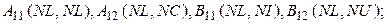
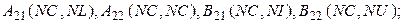
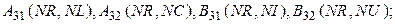
Подставляя 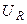 из третьей группы уравнений (3) в последнюю, представим две последние группы уравнений (3), с учетом введенных обозначений, в виде
из третьей группы уравнений (3) в последнюю, представим две последние группы уравнений (3), с учетом введенных обозначений, в виде
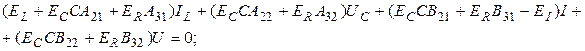
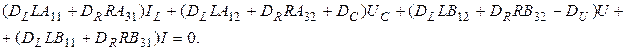
Поскольку элементы векторов 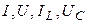 могут принимать совершенно произвольные значения, следует приравнять нулю выражения в круглых скобках; присоединяя к ним оставшиеся уравнения, получим
могут принимать совершенно произвольные значения, следует приравнять нулю выражения в круглых скобках; присоединяя к ним оставшиеся уравнения, получим
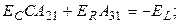
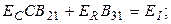
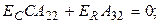
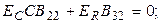
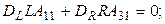
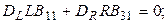
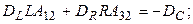
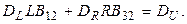
Компактная запись этой системы
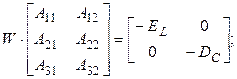 (4)
(4)
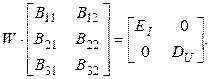
Обе группы уравнений (4) имеют одну и ту же матрицу
W= 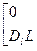
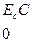
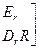
размерность которой
(NL+NC+NR)*(NZ+NK).
Определение. Если выполнено условие
NL+NC+NR=NZ+NK
и
detïWï¹0,
то цепь называется невырожденной и вырожденной, если эти условия не выполнены.
В случае невырожденной цепи системы уравнений (4) разрешимы, причем
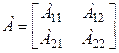 ,
, 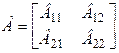 ,
, 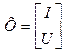 .
.
Если же цепь вырождена, необходимо преобразовать системы (4) в соответствии с рангом матрицы W.
Методологию формирования топологических матриц лучше всего проследить на примере цепи рис. 3 (а). Матрицы группы Е можно сразу выписать
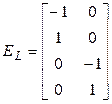 ,
, 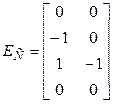 ,
, 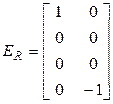 ,
, 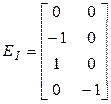 .
.
Первые строки этих матриц формируются на основе 2-го узла цепи. Ток через элемент 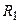 втекает в этот узел. Поэтому в матрице элемент первой строки и первого столбца равен 1. Ток через элемент
втекает в этот узел. Поэтому в матрице элемент первой строки и первого столбца равен 1. Ток через элемент 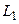 вытекает из этого узла. Поэтому в матрице
вытекает из этого узла. Поэтому в матрице 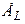 элемент первой строки и первого столбца равен -1. Все остальные элементы первых строк равны нулю, поскольку другие элементы цепи с узлом не связаны. Аналогично формируются элементы других строк матриц группы Е.
элемент первой строки и первого столбца равен -1. Все остальные элементы первых строк равны нулю, поскольку другие элементы цепи с узлом не связаны. Аналогично формируются элементы других строк матриц группы Е.
Прежде чем формировать матрицы группы D, необходимо построить методологию выделения контуров цепи. Структура цепи рассматриваемого примера представлена на рис. 3 (б) в виде трех массивов. Один из этих массивов характеризует тип элемента. Два других массива из целых чисел содержат номера узлов соответствующих элементов. Массивы 3 (в) формируются следующим образом. Выбираем все элементы, имеющие узлы с каким-то одним номером (выбран узел 7). Эти элементы располагают так, чтобы узлы 7 находились в одной строке (вверху). Так формируется первый уровень. Второй уровень образуют элементы с узлами, расположенными в нижней строке первого уровня (узлы 4, 1, 6). Причем эти узлы располагаются в верхней строке. Узлы нижней строки второго уровня служат основой для формирования элементов третьего уровня и т.д. Структура массива рис. 3 (в) представляется в виде корневого дерева рис. 3 (г). Пусть 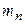 - число повторяющихся узлов с номером n на всех уровнях дерева. Для рассматриваемого примера имеем
- число повторяющихся узлов с номером n на всех уровнях дерева. Для рассматриваемого примера имеем
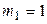 ,
, 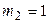 ,
, 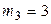 ,
, 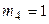 ,
, 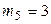 ,
, 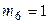 ,
,
общее число контуров, для которых записывается 2-ой закон Кирхгофа
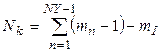 ,
,
где NY-число всех узлов, 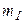 - число контуров, содержащих источники тока.
- число контуров, содержащих источники тока.
Формирование контура начинается с узла, расположенного на самом низком уровне движением вверх, до корня дерева, а затем движением вниз до узла с тем же номером. Для рассматриваемой цепи из четырех возможных контуров два содержат источники тока ( 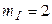 ). Два других выписаны на рис. 3 (д). Топологические матрицы группы D имеют вид
). Два других выписаны на рис. 3 (д). Топологические матрицы группы D имеют вид
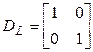 ;
; 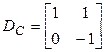 ;
; 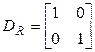 ;
; 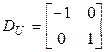 .
.
Рассмотрим, как формируются первые строки этих матриц. Для этого используем первый контур. Поскольку он содержит единственный индуктивный элемент 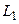 и знак напряжения на этом элементе будет положителен (противоположен знаку тока), то
и знак напряжения на этом элементе будет положителен (противоположен знаку тока), то 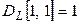 ,
, 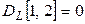 . Контур содержит 2 емкостных элемента с положительным напряжением на них, поэтому
. Контур содержит 2 емкостных элемента с положительным напряжением на них, поэтому 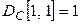 ,
, 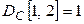 Аналогично формируются другие элементы матриц группы D.
Аналогично формируются другие элементы матриц группы D.
Рассмотренную методику формирования математической модели можно реализовать на ЭВМ и тем самым автоматизировать процесс формирования модели. В принципе эта методика не изменится, если к элементам рис. 2 добавить ключевые (управляемый ключ, диод). Если же цепь содержит транзисторы, тиристоры, трансформаторы и т.д., то можно использовать схемы замещения этих элементов из 2-х полюсных компонент.
Дата добавления: 2022-02-05; просмотров: 1068;











