Проекция силы на ось и на плоскость
Проекция силы (как и любого другого вектора) на ось есть алгебраическая величина, равная произведению модуля силы на косинус угла между силой и положительным направлением оси.Если этот угол острый – проекция положительна, если тупой – отрицательна, а если сила перпендикулярна оси – ее проекция на ось равна нулю.Так, для сил, изображенных на рисунке 1_19:
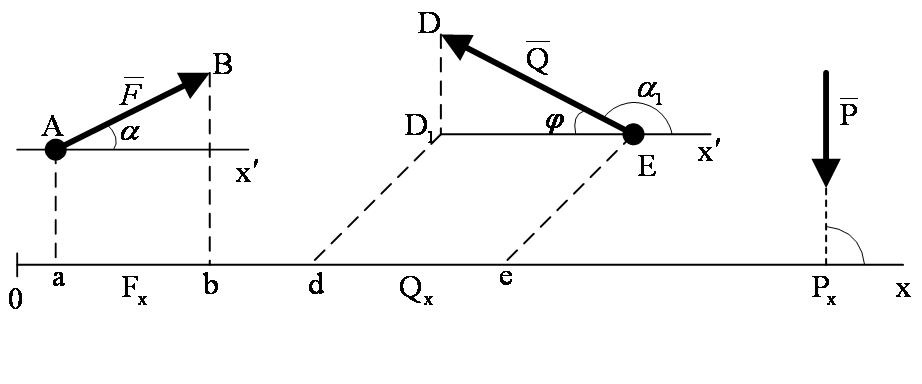
 , ,  , , 
| (1.3) |
Проекцией силы 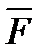 на плоскость Оху является вектор
на плоскость Оху является вектор 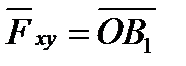 , заключенный между проекциями начала и конца силы
, заключенный между проекциями начала и конца силы 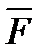 на эту плоскость(рисунок 1_20).
на эту плоскость(рисунок 1_20).
Таким образом, в отличие от проекции силы на ось, проекция силы на плоскость есть величина векторная, так как она характеризуется не только своими числовыми значениями, но и направлением в плоскости Оху. По модулю 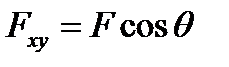 , где
, где 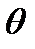 – угол между направлением силы
– угол между направлением силы 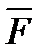 и ее проекцией
и ее проекцией 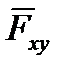 .
.
Аналитический способ задания и сложения сил
Для аналитического задания силы необходимо выбрать систему координатных осей Oxyz, по отношению к которой будет определяться направление силы в пространстве.
В механике мы будем пользоваться правой системой координат, т. е. такой системой, в которой кратчайшее совмещение оси Ох с осью Оу происходит, если смотреть с положительного конца оси Oz, против хода часовой стрелки (рисунок 1_21).
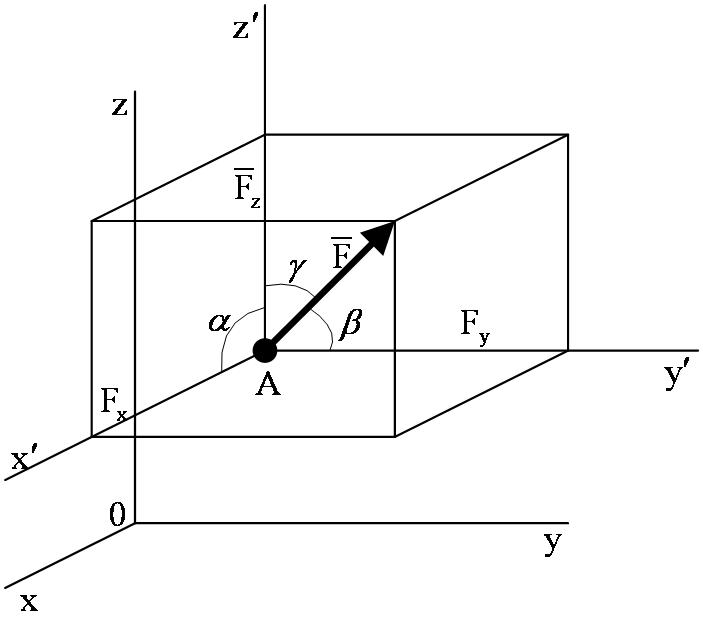
Вектор, изображающий силу 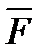 , можно построить, если известны модуль F этой силы и углы
, можно построить, если известны модуль F этой силы и углы 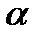 ,
, 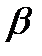 ,
, 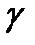 , которые сила образует с координатными осями. Таким образом, величины
, которые сила образует с координатными осями. Таким образом, величины 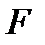 ,
, 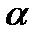 ,
, 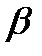 ,
, 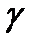 , и задают силу
, и задают силу 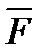 . Точка
. Точка 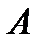 приложения силы должна быть задана отдельно ее координатами
приложения силы должна быть задана отдельно ее координатами 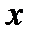 ,
, 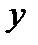 ,
, 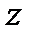 .
.
Для решения задач механики удобнее задавать силу ее проекциями 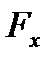 ,
, 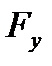 ,
, 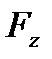 на координатные оси. Зная эти проекции, можно определить модуль силы и углы, которые она образует с координатными осями, по формулам:
на координатные оси. Зная эти проекции, можно определить модуль силы и углы, которые она образует с координатными осями, по формулам:
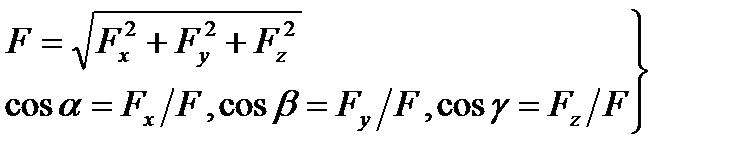
| (1.4) |
Если все рассматриваемые силы расположены в одной плоскости, то каждую из сил можно задать ее проекциями на две оси 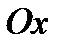 и
и 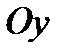 . Тогда формулы, определяющие силу по ее проекциям, примут вид:
. Тогда формулы, определяющие силу по ее проекциям, примут вид:
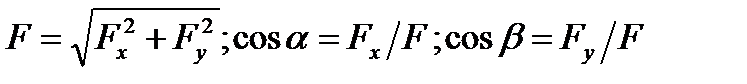
| (1.5) |
Переход от зависимостей между векторами к зависимостям между их проекциями осуществляется с помощью следующей теоремы геометрии: проекция вектора суммы на какую-нибудь ось равна алгебраической сумме проекций слагаемых векторов на ту же ось. Согласно этой теореме, если 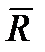 есть сумма сил
есть сумма сил 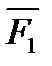 ,
, 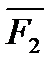 , . . . ,
, . . . , 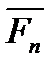 ,т. е.
,т. е. 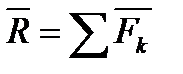 , то
, то
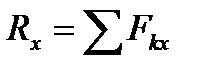 , , 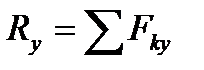 , , 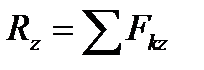
| (1.6) |
Зная 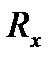 ,
, 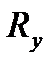 и
и 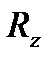 , по формулам (1.4) находим:
, по формулам (1.4) находим:
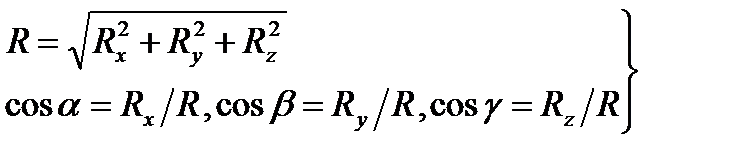
| (1.7) |
Если силы заданы их модулями и углами с осями, то для применения аналитического метода сложения надо предварительно вычислить проекции этих сил на координатные оси.
Равновесие системы сходящихся сил
Для равновесия системы сходящихся сил, приложенных к твердому телу, необходимо и достаточно, чтобы равнодействующая, а, следовательно, и главный вектор этих сил были равны нулю. Условия, которым при этом должны удовлетворять сами силы, можно выразить в геометрической или в аналитической форме.
Так как главный вектор 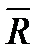 системы сил определяется как замыкающая сторона силового многоугольника, построенного из этих сил, то
системы сил определяется как замыкающая сторона силового многоугольника, построенного из этих сил, то 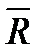 может обратиться в нуль только тогда, когда конец последней силы в многоугольнике совпадает с началом первой силы, т. е. когда многоугольник замкнется.
может обратиться в нуль только тогда, когда конец последней силы в многоугольнике совпадает с началом первой силы, т. е. когда многоугольник замкнется.
Следовательно, геометрическое условие равновесия формулируется следующим образом: для равновесия системы сходящихся сил необходимо и достаточно, чтобы силовой многоугольник, построенный из этих сил, был замкнутым.
Аналитически модуль главного вектора системы сил определяется формулой 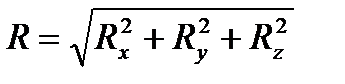 . Так как под корнем стоит сумма положительных слагаемых, то
. Так как под корнем стоит сумма положительных слагаемых, то 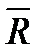 обратится в нуль только тогда, когда одновременно
обратится в нуль только тогда, когда одновременно 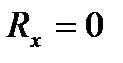 ,
, 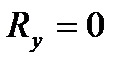 ,
, 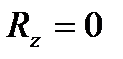 ,т.е., как это следует из формул (1.6), когда действующие на тело силы будут удовлетворять равенствам:
,т.е., как это следует из формул (1.6), когда действующие на тело силы будут удовлетворять равенствам:
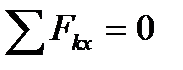 , , 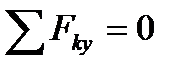 , , 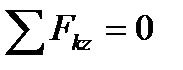
| (1.8) |
Равенства (1.8) выражают условия равновесия в аналитической форме: для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы суммы проекций этих сил на каждую из трех координатных осей были равны нулю.
Если все действующие на тело сходящиеся силы лежат в одной плоскости, то они образуют плоскую систему сходящихся сил.В случае плоской системы сходящихся сил получим, очевидно, только два условия равновесия:
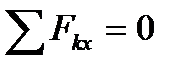 , , 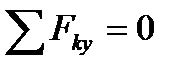
| (1.9) |
При решении задач статики иногда удобно пользоваться теоремой о трех силах: если твердое тело находится в равновесии под действием трех непараллельных сил, лежащих в одной плоскости, то линии действия этих сил пересекаются в одной точке.
Для доказательства теоремы рассмотрим сначала какие-нибудь две из действующих на тело сил, например  и
и  . Так как по условиям теоремы эти силы лежат в одной плоскости и не параллельны, то их линии действия пересекаются в некоторой точке А (рисунок 1_22).
. Так как по условиям теоремы эти силы лежат в одной плоскости и не параллельны, то их линии действия пересекаются в некоторой точке А (рисунок 1_22).
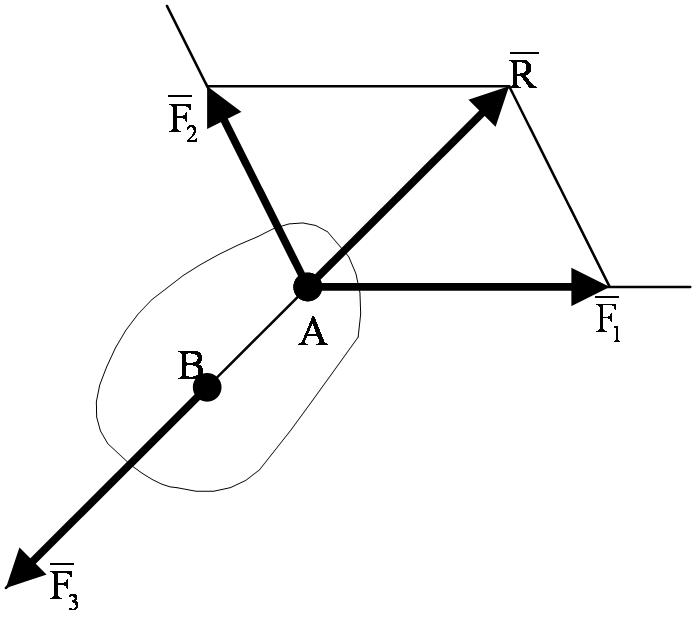
Приложим силы 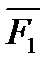 и
и 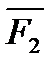 в этой точке и заменим их равнодействующей
в этой точке и заменим их равнодействующей 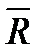 . Тогда на тело будут действовать две силы: сила
. Тогда на тело будут действовать две силы: сила 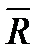 и сила
и сила 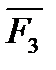 ,приложенная в какой-то точке В тела. Если тело при этом находится в равновесии, то силы
,приложенная в какой-то точке В тела. Если тело при этом находится в равновесии, то силы 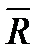 и
и 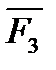 должны быть направлены по одной прямой, т.е. вдоль АВ. Следовательно, линия действия силы
должны быть направлены по одной прямой, т.е. вдоль АВ. Следовательно, линия действия силы 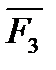 тоже проходит через точку А, что и требовалось доказать.
тоже проходит через точку А, что и требовалось доказать.
Обратная теорема места не имеет, т. е. если линии действия трех сил пересекаются в одной точке, то тело под действием этих сил может и не находиться в равновесии; следовательно, теорема выражает только необходимоеусловие равновесия тела под действием трех сил.
Решение задач статики
Решаемые методами статики задачи могут быть одного из следующих двух типов:
1) задачи, в которых известны (полностью или частично) действующие на тело силы и требуется найти, в каком положении или при каких соотношениях между действующими силами тело будет находиться в равновесии
2) задачи, в которых известно, что тело заведомо находится в равновесии и требуется найти, чему равны при этом все или некоторые из действующих на тело сил.
Реакции связей являются величинами, наперед неизвестными во всех задачах статики.
Приступая к решению любой задачи, следует прежде всего установить, равновесие какого тела (или каких тел) надо рассмотреть, чтобы найти искомые величины.
Процесс решения сводится к следующим операциям:
1) Выбор тела (или тел), равновесие которого должно быть рассмотрено.
Когда заданные силы действуют на одно тело, а искомые на другое или когда те и другие силы действуют одновременно на несколько тел, может оказаться необходимым рассмотреть равновесие системы этих тел или последовательно равновесие каждого тела в отдельности.
2) Изображение действующих сил
Установив, равновесие какого тела или тел рассматривается (и только после этого), следует на чертеже изобразить все действующие на это тело, (или тела) внешние силы, включая как заданные, так и искомые силы, в том числе реакции всех связей.
3) Составление условий равновесия
4) Определение искомых величин, проверка правильности решения и исследование полученных результатов
Все расчеты при решении задач рекомендуется, как правило, производить в общем виде (алгебраически). Тогда для искомых величин будут получаться формулы, дающие возможность проанализировать найденные результаты. Кроме того, решение в общем виде позволяет иногда обнаружить сделанные ошибки путем проверки размерностей (размерности каждого из слагаемых в обеих частях равенства должны быть одинаковыми). Числа, если решение производится в общем виде, подставляются только в окончательные результаты.
Для решения задач на равновесие системы сходящихся сил можно пользоваться геометрическим или аналитическим методом.
Геометрическим методом удобно пользоваться, когда общее число действующих на тело сил (и заданных, и искомых) равно трем. При равновесии треугольник, построенный из этих сил, должен быть замкнутым (построение следует начинать с заданной силы). Решая этот треугольник, найдем искомые величины.
Аналитическим методом можно пользоваться при любом числе приложенных сил. Для составления условий равновесия, которых в случае плоской системы сходящихся сил будет два, а в случае пространственной системы три, надо сначала выбрать координатные оси. Этот выбор можно производить произвольно, но полученные уравнения будут решаться проще, если одну из осей направить перпендикулярно какой-либо неизвестной силе.
Момент силы относительно центра (или точки)
Введем важное понятие о моменте силы относительно точки.
Если под действием приложенной силы тело может совершать вращение вокруг некоторой точки, то момент силы относительно этой точки будет характеризовать вращательный эффект силы.
Рассмотрим силу  , приложенную к телу в точке
, приложенную к телу в точке 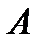 (рисунок 1_23).
(рисунок 1_23).
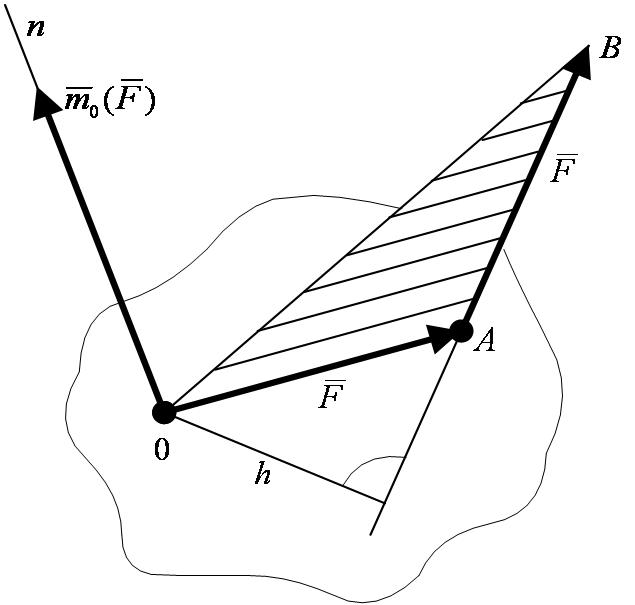
Из некоторого центра  опустим перпендикуляр на линию действия силы
опустим перпендикуляр на линию действия силы  ; длину
; длину 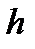 этого перпендикуляра называют плечом силы
этого перпендикуляра называют плечом силы 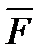 относительно центра
относительно центра  . Момент силы относительно центра
. Момент силы относительно центра  определяется: 1) модулем момента, равным произведению
определяется: 1) модулем момента, равным произведению 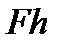 ; 2) положением в пространстве плоскости
; 2) положением в пространстве плоскости 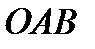 («плоскости поворота»), проходящей через центр
(«плоскости поворота»), проходящей через центр  и силу
и силу 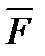 ; 3) направлением поворота в этой плоскости.
; 3) направлением поворота в этой плоскости.
Из геометрии известно, что положение плоскости в пространстве определяется направлением нормали (перпендикуляра) к этой плоскости. Таким образом, момент силы относительно центра характеризуется не только его числовым значением, но и направлением в пространстве, т. е. является величиной векторной.
Таким образом, моментом силы 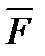 относительно центра
относительно центра  называется приложенный в центре
называется приложенный в центре  вектор
вектор 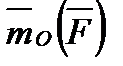 , модуль которого равен произведению модуля
, модуль которого равен произведению модуля 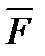 силы на ее плечо
силы на ее плечо 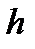 и который направлен перпендикулярно плоскости, проходящей через центр
и который направлен перпендикулярно плоскости, проходящей через центр  и силу, в ту сторону, откуда сила видна стремящейся повернуть тело вокруг центра
и силу, в ту сторону, откуда сила видна стремящейся повернуть тело вокруг центра  против хода часовой стрелки (рисунок 1_23).
против хода часовой стрелки (рисунок 1_23).
Согласно этому определению
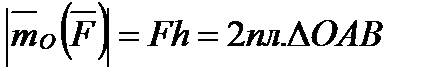
| (1.10) |
Последний результат следует из того, что пл. 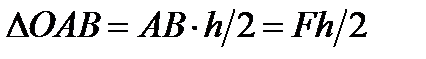 . Измеряется момент силы в ньютон-метрах (Н·м).
. Измеряется момент силы в ньютон-метрах (Н·м).
Найдем формулу, выражающую вектор 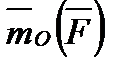 . Для этого рассмотрим векторное произведение
. Для этого рассмотрим векторное произведение 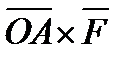 векторов
векторов 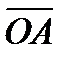 и
и 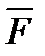 . По определению векторным произведением
. По определению векторным произведением 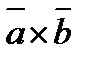 векторов
векторов 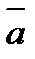 и
и 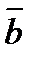 называется вектор
называется вектор 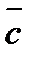 , равный по модулю площади параллелограмма, построенного на векторах
, равный по модулю площади параллелограмма, построенного на векторах 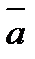 и
и 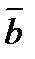 , и направленный перпендикулярно плоскости этих векторов в ту сторону, откуда кратчайшее совмещение
, и направленный перпендикулярно плоскости этих векторов в ту сторону, откуда кратчайшее совмещение 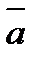 с
с 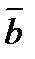 видно происходящим против хода часовой стрелки. Модуль с определяется еще равенством
видно происходящим против хода часовой стрелки. Модуль с определяется еще равенством 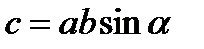 где
где 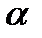 – угол между векторами
– угол между векторами 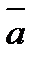 и
и 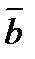 . Если векторы
. Если векторы 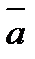 и
и 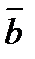 параллельны, то
параллельны, то 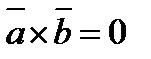 . Тогда
. Тогда 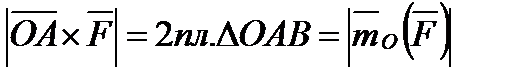 .
.
Направлен вектор 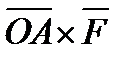 перпендикулярно плоскости
перпендикулярно плоскости 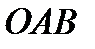 в ту сторону, откуда кратчайшее совмещение
в ту сторону, откуда кратчайшее совмещение 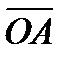 с
с 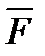 (если их отложить от одной точки) видно происходящим против хода часовой стрелки т.е. так же, как вектор
(если их отложить от одной точки) видно происходящим против хода часовой стрелки т.е. так же, как вектор 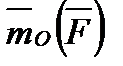 . Следовательно, векторы
. Следовательно, векторы 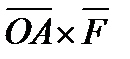 и
и 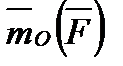 совпадают и по модулю, и по направлению, и, как легко видеть, по размерности, т. е. выражают одну и ту же величину. Отсюда
совпадают и по модулю, и по направлению, и, как легко видеть, по размерности, т. е. выражают одну и ту же величину. Отсюда
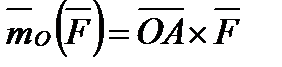 или или 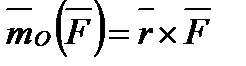
| (1.11) |
где 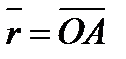 – радиус-вектор точки
– радиус-вектор точки 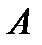 , проведенный из центра
, проведенный из центра  .
.
Таким образом, момент силы 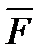 относительно центра
относительно центра  равен векторному произведению радиуса-вектора
равен векторному произведению радиуса-вектора 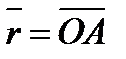 , проведенного из центра
, проведенного из центра  в точку
в точку 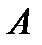 , где приложена сила, на саму силу. Этот результат может служить другим определением понятия о моменте силы относительно центра.
, где приложена сила, на саму силу. Этот результат может служить другим определением понятия о моменте силы относительно центра.
Отметим следующие свойства момента силы: 1) момент силы относительно центра не изменяется при переносе точки приложения силы вдоль ее линии действия; 2) момент силы относительно центра  равен нулю или когда сила равна нулю, или когда линия действия силы проходит через центр
равен нулю или когда сила равна нулю, или когда линия действия силы проходит через центр  (плечо равно нулю).
(плечо равно нулю).
Пара сил. Момент пары
Термин пара сил(рисунок 1_24).
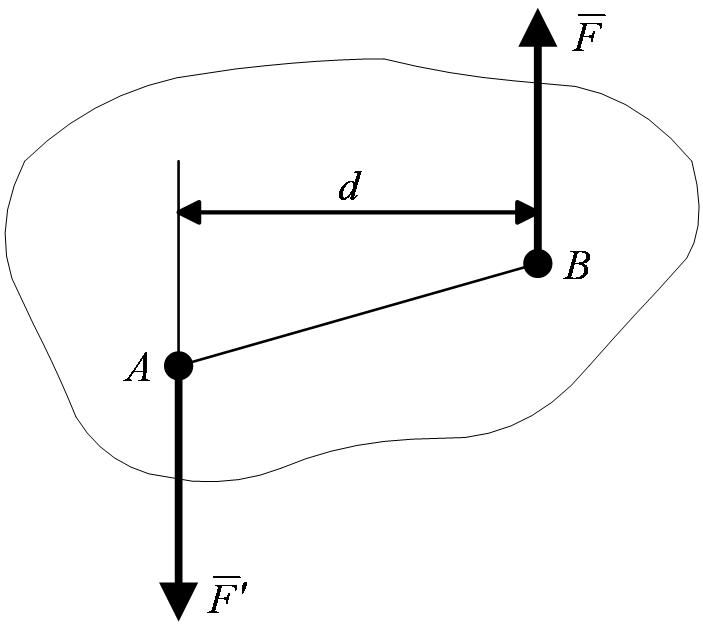
Система сил  ,
,  , образующих пару, очевидно, не находится в равновесии (эти силы не направлены вдоль одной прямой). В то же время пара сил не имеет равнодействующей, поскольку, как будет доказано, равнодействующая любой системы сил равна ее главному вектору
, образующих пару, очевидно, не находится в равновесии (эти силы не направлены вдоль одной прямой). В то же время пара сил не имеет равнодействующей, поскольку, как будет доказано, равнодействующая любой системы сил равна ее главному вектору 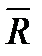 , т. е. сумме этих сил, а для пары
, т. е. сумме этих сил, а для пары 
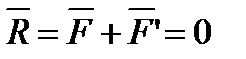 . Поэтому свойства пары сил, как особой меры механического взаимодействия тел, должны быть рассмотрены отдельно.
. Поэтому свойства пары сил, как особой меры механического взаимодействия тел, должны быть рассмотрены отдельно.
Термин плоскость действия пары.
Термин плечо пары (рисунок 1_24).
Действие пары сил на твердое тело сводится к некоторому вращательному эффекту, который характеризуется моментом пары. Этот момент определяется: 1) его модулем, равным произведению 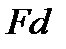 ; 2) положением в пространстве плоскости действия пары; 3) направлением поворота пары в этой плоскости. Таким образом, как и момент силы относительно центра, это величина векторная.
; 2) положением в пространстве плоскости действия пары; 3) направлением поворота пары в этой плоскости. Таким образом, как и момент силы относительно центра, это величина векторная.
Термин момент пары (рисунок 1_25).
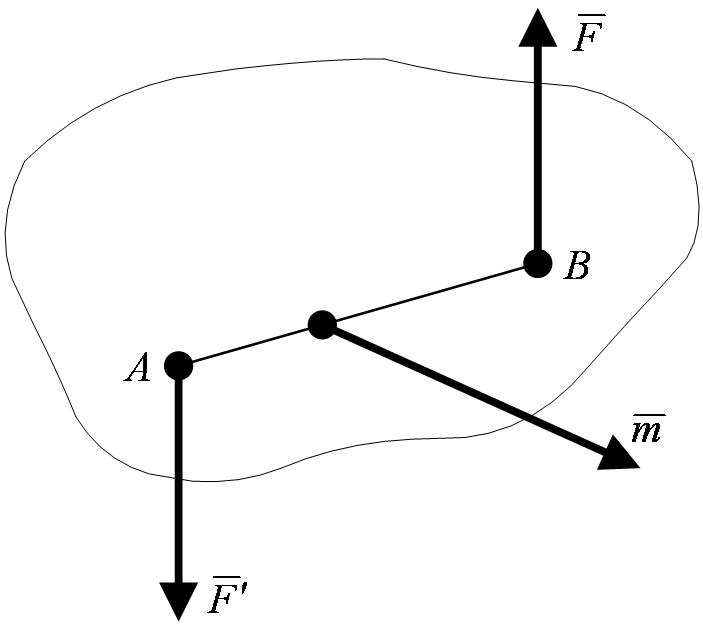
Заметим еще, что, так как плечо силы 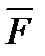 относительно точки
относительно точки 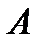 равно
равно 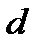 , а плоскость, проходящая через точку
, а плоскость, проходящая через точку 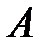 и силу
и силу 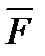 , совпадает с плоскостью действия пары, то одновременно
, совпадает с плоскостью действия пары, то одновременно 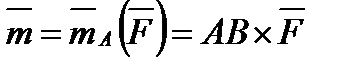 . Но в отличие от момента силы вектор
. Но в отличие от момента силы вектор 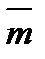 , как будет показано ниже, может быть приложен в любой точке (такой вектор называется свободным). Измеряется момент пары, как и момент силы, в ньютон-метрах.
, как будет показано ниже, может быть приложен в любой точке (такой вектор называется свободным). Измеряется момент пары, как и момент силы, в ньютон-метрах.
Покажем, что моменту пары можно дать другое выражение: момент пары равен сумме моментов относительно любого центра  сил, образующих пару, т. е.
сил, образующих пару, т. е.
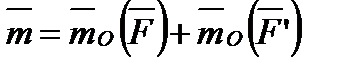
| (1.12) |
Для доказательства проведем из произвольной точки  (рисунок 1_26) радиусы-векторы
(рисунок 1_26) радиусы-векторы 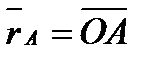 и
и 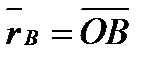 .
.
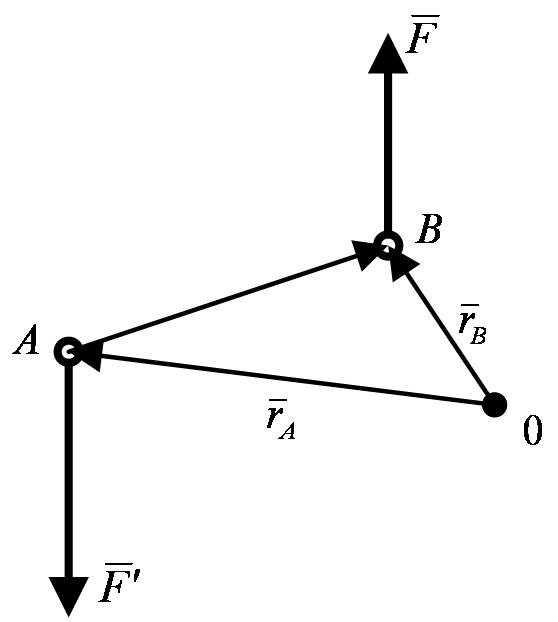
Тогда согласно формуле (1.11), учтя еще, что 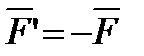 , получим
, получим 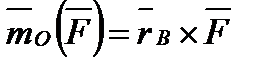 ,
, 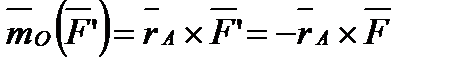 и, следовательно,
и, следовательно, 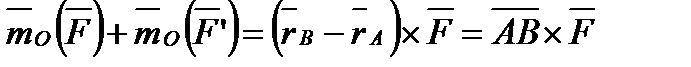 .
.
Так как 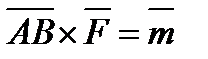 , то справедливость равенства (1.12) доказана. Отсюда, в частности, следует уже отмеченный выше результат:
, то справедливость равенства (1.12) доказана. Отсюда, в частности, следует уже отмеченный выше результат:
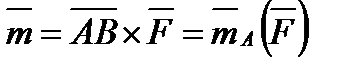 или или 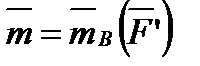
| (1.13) |
т. е. что момент пары равен моменту одной из ее сил относительно точки приложения другой силы. Отметим еще, что модуль момента пары
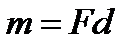
| (1.14) |
Если принять, что действие пары сил на твердое тело (ее вращательный эффект) полностью определяется значением суммы моментов сил пары относительно любого центра  , то из формулы (1.12) следует, что две пары сил, имеющие одинаковые моменты, эквивалентны, т.е. оказывают на тело одинаковое механическое действие. Иначе это означает, что две пары сил, независимо от того, где каждая из них расположена в данной плоскости (или в параллельных плоскостях) и чему равны в отдельности модули их сил и их плечи, если их моменты имеют одно и то же значение
, то из формулы (1.12) следует, что две пары сил, имеющие одинаковые моменты, эквивалентны, т.е. оказывают на тело одинаковое механическое действие. Иначе это означает, что две пары сил, независимо от того, где каждая из них расположена в данной плоскости (или в параллельных плоскостях) и чему равны в отдельности модули их сил и их плечи, если их моменты имеют одно и то же значение 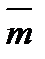 , будут эквивалентны. Так как выбор центра
, будут эквивалентны. Так как выбор центра  произволен, то вектор
произволен, то вектор 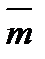 можно считать приложенным в любой точке, т. е. это вектор свободный.
можно считать приложенным в любой точке, т. е. это вектор свободный.
В дальнейшем будем обычно на чертеже вместо пары изображать полностью ее характеризующий вектор 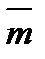 . При этом модуль
. При этом модуль 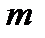 определяет модуль момента пары (формула 1.14), а направление
определяет модуль момента пары (формула 1.14), а направление 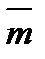 определяет плоскость действия пары и направление поворота в этой плоскости.
определяет плоскость действия пары и направление поворота в этой плоскости.
Из формулы (1.12) следует еще, что если на тело действует несколько пар с моментами 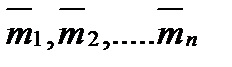 , то сумма моментов всех сил, образующих эти пары, относительно любого центра будет равна
, то сумма моментов всех сил, образующих эти пары, относительно любого центра будет равна 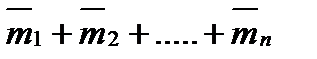 , а следовательно, вся совокупность этих пар эквивалентна одной паре с моментом
, а следовательно, вся совокупность этих пар эквивалентна одной паре с моментом 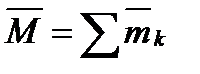 . Этот результат выражает теорему о сложении.
. Этот результат выражает теорему о сложении.
Дата добавления: 2021-06-28; просмотров: 1173;











