Работа силы. Мощность

Для характеристики действия, оказываемого силой на тело при некотором его перемещении, вводится понятие о работе силы, широко используемое не только в механике. Сначала введем понятие об элементарной работе.

Элементарной работой силы 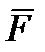, приложенной в точке М (рисунок 3_1),

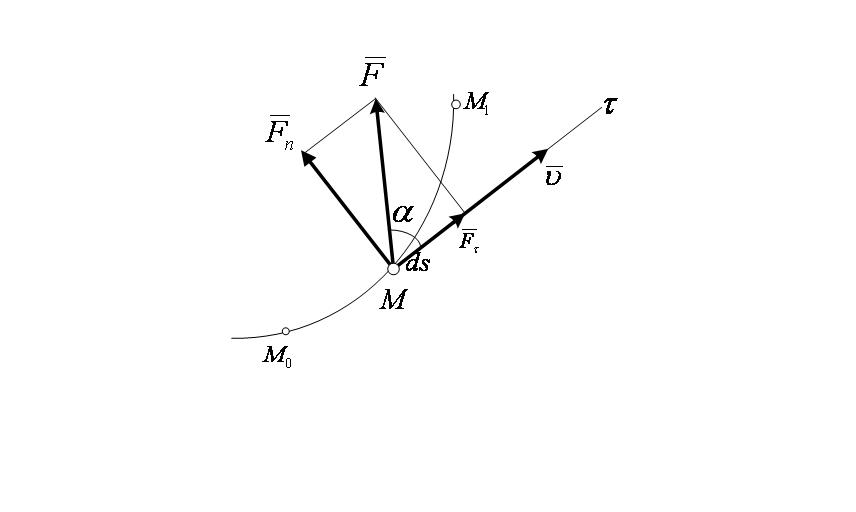
называется скалярная величина

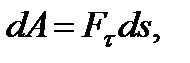
(3.23)

где 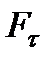– проекция силы 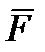на касательную 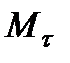к траектории точки М, направленную в сторону перемещения этой точки (или проекция 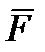на направление скорости точки М);

ds – модуль элементарного перемещения точки М.

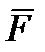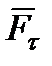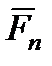Такое определение соответствует представлению о работе как о мере того действия силы, которое приводит к изменению модуля скорости точки. Если разложить силу на составляющие и , то изменять модуль скорости будет 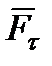, так как 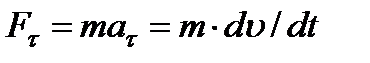(составляющая 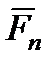, изменяет или направление вектора, или при несвободном движении – силу давления на связь).

Замечая, что 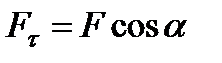а, где 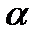– угол между 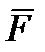и 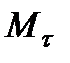, получим из другое выражение для :

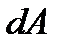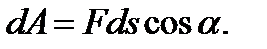
(3.24)

Если угол 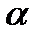острый, то работа положительна. В частности, при 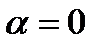элементарная работа .

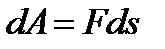Если угол 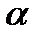тупой, то работа отрицательна. В частности, при 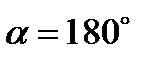элементарная работа .

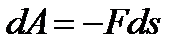Если угол 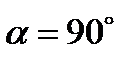, т. е. если сила направлена перпендикулярно перемещению, то элементарная работа силы равна нулю.

Знак работы имеет следующий смысл: работа положительна, когда составляющая 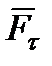, направлена в сторону движения (сила ускоряет движение); работа отрицательна, когда составляющая 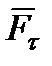направлена противоположно направлению движения (сила замедляет движение);

Если учесть, что 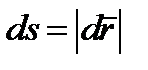, где 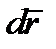– вектор элементарного перемещения точки, то равенство (3.24) можно представить в виде

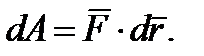
(3.25)

Следовательно, элементарная работа силы равна скалярному произведению силы на вектор элементарного перемещения точки ее приложения.

Если в формуле (3.25) выразить скалярное произведение через проекции векторов 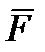и 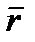на координатные оси и учесть, что 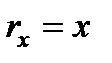, , 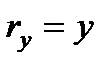, 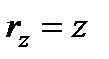то получим аналитическое выражение элементарной работы

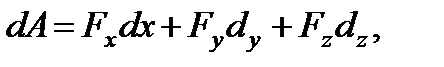
(3.26)

в котором х, у, z – координаты точки приложения силы .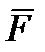

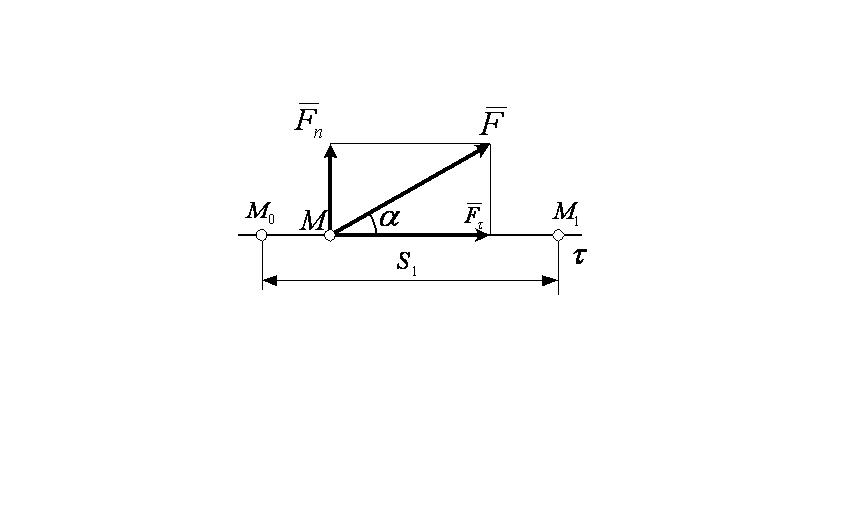
Работа силы на любом конечном перемещении 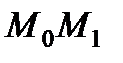(рисунок 3_1)

вычисляется как предел интегральной суммы соответствующих элементарных работ

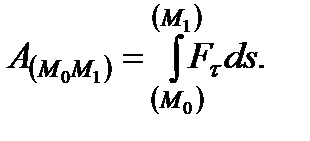
(3.27)

Следовательно, работа силы на любом перемещении 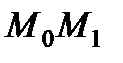равна взятому вдоль этого перемещения интегралу от элементарной работы. Пределы интеграла соответствуют значениям переменных интегрирования в точках 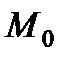и 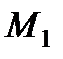(точнее говоря, интеграл берется вдоль кривой 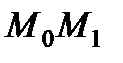, т. е. является криволинейным).

Если величина 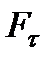постоянна 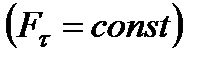, то из (3.27), обозначая перемещение 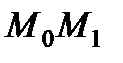через 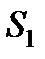, получим .

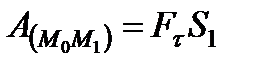В частности, такой случай может иметь место, когда действующая сила постоянна по модулю и направлению 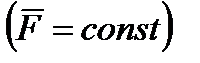, а точка, к которой приложена сила, движется прямолинейно (рисунок 3_2).

В этом случае 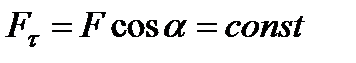и

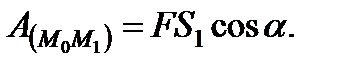
(3.28)

Единицей измерения работы является в СИ является 1 джоуль.

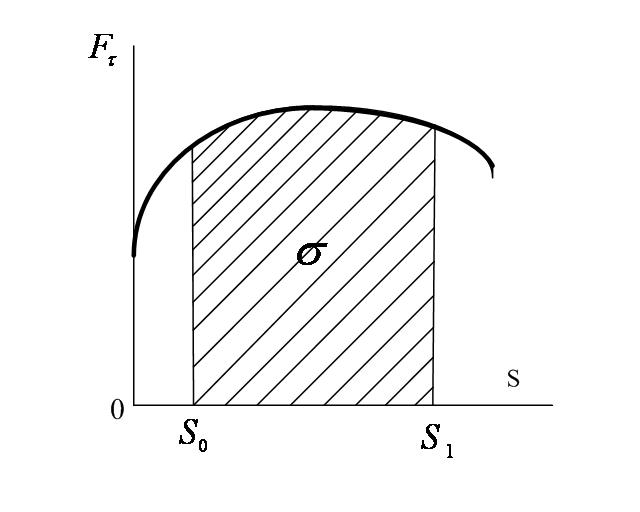
Графический способ вычислении работы. Если сила зависит от расстояния s и известен график зависимости 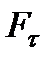от s (рисунок 3_3), то работу силы можно вычислить графически.

Пусть в положении 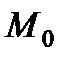точка находится от начала отсчета на расстоянии 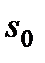, а в положении 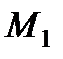на расстоянии 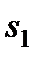. Тогда по формуле (3.27), учитывая геометрический смысл интеграла, получим

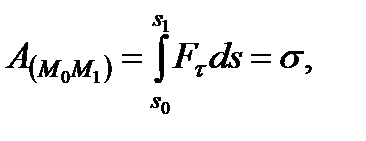
где величина заштрихованной на рисунке 3_3 площади, умноженной на масштабный коэффициент.

Термин мощность.

Если работа совершается равномерно, то мощность 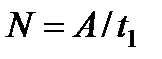, где 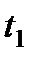– время, в течение которого произведена работа А. В общем случае

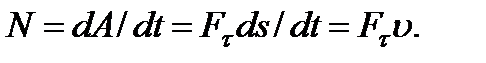
(3.29)

Следовательно, мощность равна произведению касательной составляющей силы на скорость.

Единицей измерения мощности в СИ является ватт (1 Вт=1 Дж/с). В технике за единицу мощности часто принимается 1 л. с., равная 736 Вт.

Работу, произведенную машиной, можно измерять произведением ее мощности на время работы. Отсюда возникла употребительная в технике единица измерения работы киловатт-час (1 кВтч=3,6 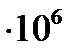Дж).

Из равенства 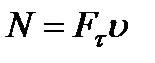видно, что у двигателя, имеющего данную мощность 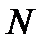, сила тяги 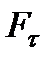будет тем больше, чем меньше скорость 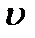. Поэтому, например, на подъеме или на плохом участке дороги у автомобиля включают низшие передачи, позволяющие при полной мощности двигаться с меньшей скоростью и развивать большую силу тяги.