Лекция №6 Тема 2.3 Кинематика плоскопараллельного движения абсолютно твердого тела и сложного движения точки
Вопросы:
2.3.1. Уравнения движения плоской фигуры. Распределение линейных скоростей точек плоской фигуры при плоском движении. Теорема о сложении скоростей. Мгновенный центр скоростей
2.3.2. Распределение линейных ускорений точек плоской фигуры при плоском движении.
2.3.3. Абсолютное, переносное и относительное движения. Переносная, относительная и абсолютная скорости движения точки. Теорема о сложении скоростей.
2.3.4. Переносное, относительное, кориолисово и абсолютное ускорения движения точки. Теорема о сложении ускорений (теорема Кориолиса).
Термин плоскопараллельное движение (рисунок 2_19).
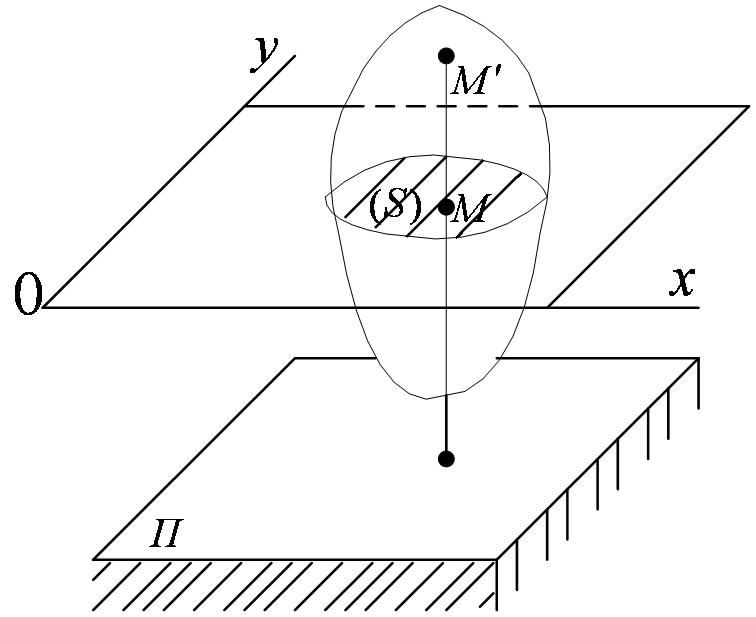
Рассмотрим сечение S тела какой-нибудь плоскостью Оху, параллельной плоскости П (рисунок 2_19). При плоскопараллельном движении все точки тела, лежащие на прямой ММ', перпендикулярной сечению S, т. е. плоскости П, движутся тождественно.
Отсюда заключаем, что для изучения движения всего тела достаточно изучить, как движется в плоскости Оху сечение S этого тела или некоторая плоская фигура S. Поэтому в дальнейшем вместо плоского движения тела будем рассматривать движение плоской фигуры S в ее плоскости, т.е. в плоскости Оху.
Положение фигуры S в плоскости Оху определяется положением какого-нибудь проведенного на этой фигуре отрезка АВ (рисунок 2_20).
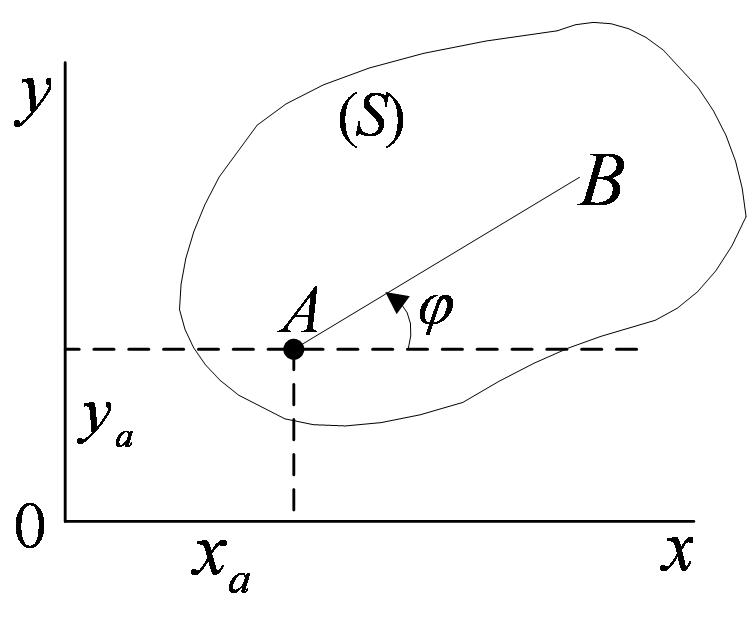
В свою очередь положение отрезка АВ можно определить, зная координаты 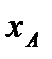 ,
, 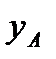 точки А и угол φ, который отрезок АВ образует с осью х. Точку A, выбранную для определения положения фигуры S, будем в дальнейшем называть полюсом.
точки А и угол φ, который отрезок АВ образует с осью х. Точку A, выбранную для определения положения фигуры S, будем в дальнейшем называть полюсом.
При движении фигуры величины 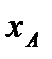 ,
, 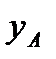 и φ будут изменяться. Чтобы знать закон движения, т. е. положение фигуры в плоскости Оху в любой момент времени, надо знать зависимости
и φ будут изменяться. Чтобы знать закон движения, т. е. положение фигуры в плоскости Оху в любой момент времени, надо знать зависимости
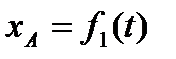 , , 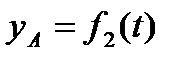 , , 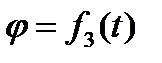 . .
| (2.37) |
Уравнения (2.37), называются уравнениями движения плоской фигуры в ее плоскости. Они же являются уравнениями плоскопараллельного движения твердого тела.
Первые два из уравнений (2.37) определяют то движение, которое фигура совершала бы при 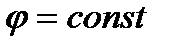 ; это, очевидно, будет поступательное движение, при котором все точки фигуры движутся так же, как полюс А. Третье уравнение определяет движение, которое фигура совершала бы при
; это, очевидно, будет поступательное движение, при котором все точки фигуры движутся так же, как полюс А. Третье уравнение определяет движение, которое фигура совершала бы при 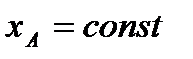 и
и 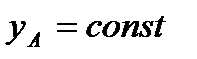 , т.е. когда полюс А неподвижен; это будет вращение фигуры вокруг полюса А. Отсюда можно заключить, что в общем случае движение плоской фигуры в ее плоскости может рассматриваться как слагающееся из поступательного движения, при котором все точки фигуры движутся так же, как полюс А, и из вращательного движения вокруг этого полюса.
, т.е. когда полюс А неподвижен; это будет вращение фигуры вокруг полюса А. Отсюда можно заключить, что в общем случае движение плоской фигуры в ее плоскости может рассматриваться как слагающееся из поступательного движения, при котором все точки фигуры движутся так же, как полюс А, и из вращательного движения вокруг этого полюса.
Основными кинематическими характеристиками рассматриваемого движения являются скорость и ускорение поступательного движения, равные скорости и ускорению полюса ( 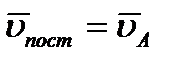 ,
, 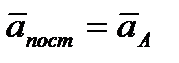 ), а также угловая скорость со и угловое ускорение вращательного движений вокруг полюса. Значения этих характеристик в любой момент времени t можно найти, воспользовавшись уравнениями (2.37).
), а также угловая скорость со и угловое ускорение вращательного движений вокруг полюса. Значения этих характеристик в любой момент времени t можно найти, воспользовавшись уравнениями (2.37).
Определение скоростей точек плоской фигуры.
Ранее было установлено, что движение плоской фигуры можно рассматривать как слагающееся из поступательного движения, при котором все точки фигуры движутся со скоростью 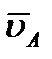 полюса А, и из вращательного движения вокруг этого полюса. Покажем, что скорость любой точки М фигуры складывается геометрически из скоростей, которые точка получает в каждом из этих движений.
полюса А, и из вращательного движения вокруг этого полюса. Покажем, что скорость любой точки М фигуры складывается геометрически из скоростей, которые точка получает в каждом из этих движений.
В самом деле, положение любой точки М фигуры определяется по отношению к осям Оху радиусом-вектором 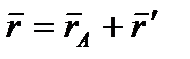 (рисунок 2_21),
(рисунок 2_21),
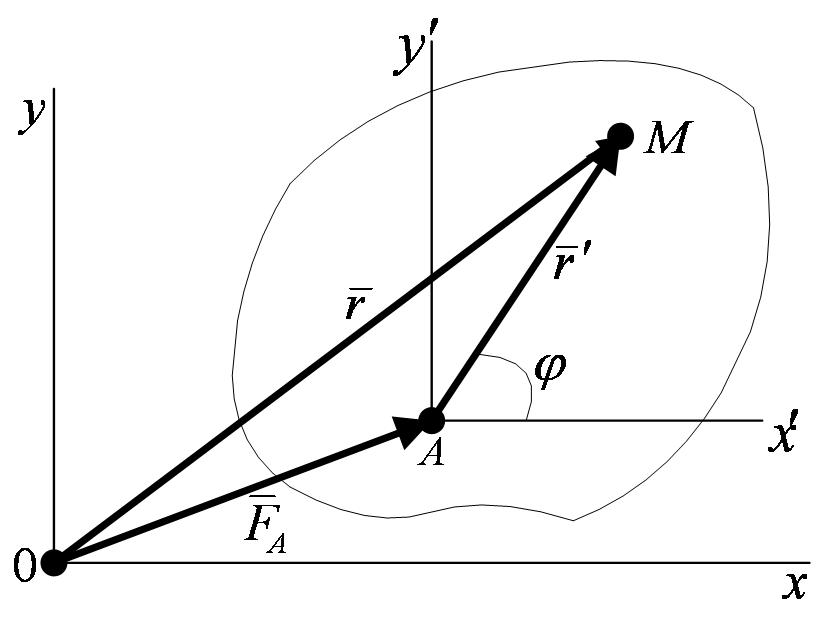
где 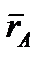 – радиус-вектор полюса А,
– радиус-вектор полюса А, 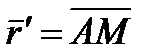 – вектор, определяющий положение точки М относительно осей Ах'у', перемещающихся вместе с полюсом А поступательно (движение фигуры по отношению к этим осям представляет собой вращение вокруг полюса А). Тогда
– вектор, определяющий положение точки М относительно осей Ах'у', перемещающихся вместе с полюсом А поступательно (движение фигуры по отношению к этим осям представляет собой вращение вокруг полюса А). Тогда 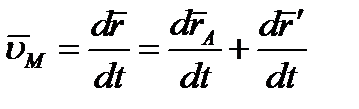 .
.
В полученном равенстве величина 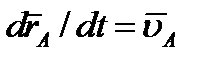 есть скорость полюса А; величина же
есть скорость полюса А; величина же 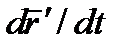 равна скорости
равна скорости 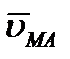 , которую точка М получает при вращении фигуры вокруг полюса А. Таким образом, из предыдущего равенства действительно следует, что
, которую точка М получает при вращении фигуры вокруг полюса А. Таким образом, из предыдущего равенства действительно следует, что
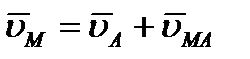
| (2.38) |
При этом скорость 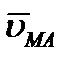 , которую точка М получает при вращении фигуры вокруг полюса A, будет:
, которую точка М получает при вращении фигуры вокруг полюса A, будет:
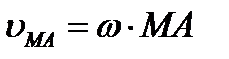 , , 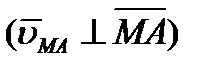
| (2.39) |
где ω – угловая скорость фигуры.
Таким образом, скорость любой точки М плоской фигуры геометрически складывается из скорости какой-нибудь другой точки А, принятой за полюс, и скорости, которую точка М получает, при вращении фигуры вокруг этого полюса. Модуль и направление скорости 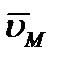 находятся построением соответствующего параллелограмма (рисунок 2_22).
находятся построением соответствующего параллелограмма (рисунок 2_22).
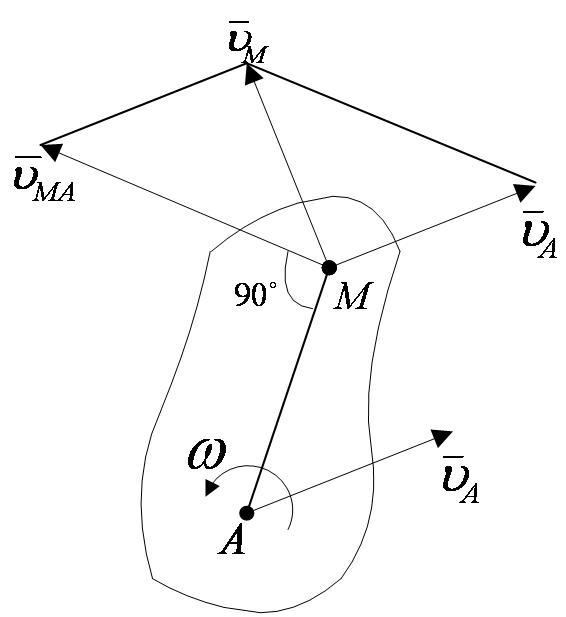
Теорема о проекциях скоростей двух точек тела
Определение скоростей точек плоской фигуры (или тела, движущегося плоскопараллельно) с помощью формулы (2.38) связано обычно с довольно сложными расчетами. Однако, исходя из этого основного результата, можно получить ряд других, практически более удобных и простых методов определения скоростей точек фигуры (или тела).
Один из таких методов дает теорема: проекции скоростей двух точек, твердого тела на ось, проходящую через эти точки, равны друг другу.
Рассмотрим какие-нибудь две точки А и В плоской фигуры (или тела). Принимая точку А за полюс (рисунок 2_23),
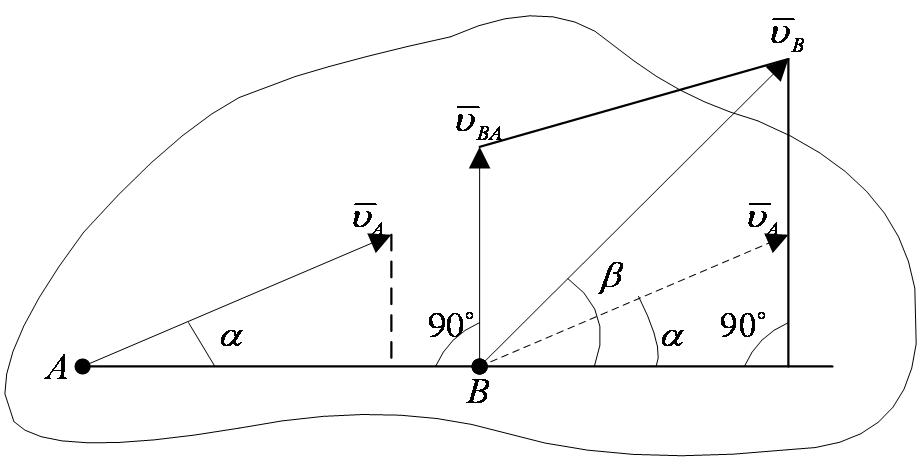
получаем по формуле (42), что 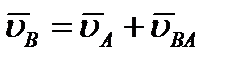 . Отсюда, проектируя обе части равенства на ось, направленную по АВ, и учитывая, что вектор
. Отсюда, проектируя обе части равенства на ось, направленную по АВ, и учитывая, что вектор 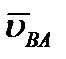 перпендикулярен АВ; находим
перпендикулярен АВ; находим
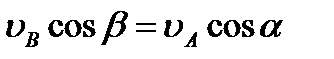
| (2.40) |
и теорема доказана.
Доказанная теорема позволяет легко находить скорость данной точки тела, если известны направление скорости этой точки и скорость какой-нибудь другой точки того же тела.
Мгновенный центр скоростей.
Другой простой и наглядный метод определения скоростей точек плоской фигуры (или тела при плоском движении) основан на понятии о мгновенном центре скоростей.
Термин мгновенный центр скоростей.
Легко убедиться, что если фигура движется непоступательно, то такая точка в каждый момент времени t существует и притом единственная. Пусть в момент времени t точки А и В плоской фигуры имеют скорости 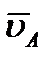 и
и 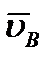 , не параллельные друг другу (рисунок 2_24).
, не параллельные друг другу (рисунок 2_24).
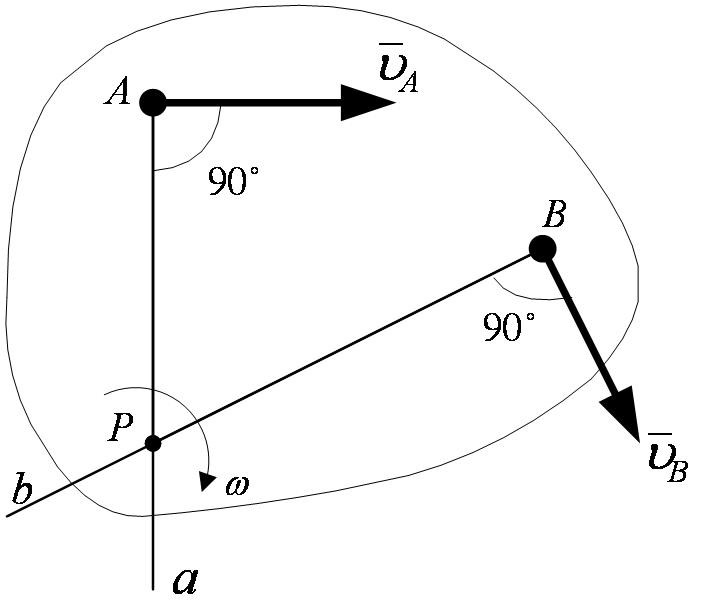
Тогда точка Р, лежащая на пересечении перпендикуляров Aa к вектору 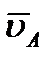 и Bb к вектору
и Bb к вектору 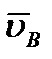 , и будет мгновенным центром скоростей, так как
, и будет мгновенным центром скоростей, так как 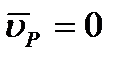 . В самом деле, если допустить, что
. В самом деле, если допустить, что 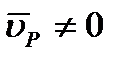 , то по теореме о проекциях скоростей вектор
, то по теореме о проекциях скоростей вектор 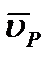 должен быть одновременно перпендикулярен и АР, (так как
должен быть одновременно перпендикулярен и АР, (так как 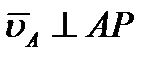 ) и ВР (так как
) и ВР (так как 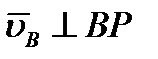 ), что невозможно. Из той же теоремы видно, что никакая другая точка фигуры в этот момент времени не может иметь скорость, равную нулю (например, для точки а проекция
), что невозможно. Из той же теоремы видно, что никакая другая точка фигуры в этот момент времени не может иметь скорость, равную нулю (например, для точки а проекция 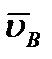 на линию Ba не равна нулю и, следовательно,
на линию Ba не равна нулю и, следовательно, 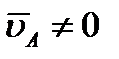 и т. д.).
и т. д.).
Если теперь в момент времени t взять точку Р за полюс, то по формуле (2.38) скорость точки А будет 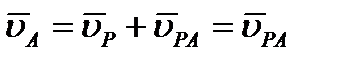 ,так как
,так как 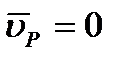 . Аналогичный результат получается для любой другой точки фигуры. Следовательно, скорости точек плоской фигуры определяются в данный момент времени так, как если бы движение фигуры было вращением вокруг мгновенного центра скоростей. При этом согласно соотношениям:
. Аналогичный результат получается для любой другой точки фигуры. Следовательно, скорости точек плоской фигуры определяются в данный момент времени так, как если бы движение фигуры было вращением вокруг мгновенного центра скоростей. При этом согласно соотношениям:
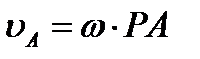 , , 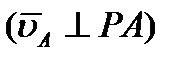 ; ; 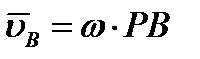 , , 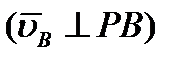 и т. д. и т. д.
| (2.41) |
Из равенств (2.41) следует еще, что
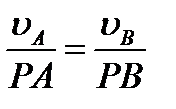
| (2.42) |
т. е. что скорости точек плоской фигуры пропорциональны их расстояниям от мгновенного центра скоростей.
Полученные результаты приводят к следующим выводам.
1) Для определения мгновенного центра скоростей надо знать только направления скоростей 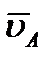 и
и 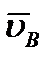 каких-нибудь двух точек А и В плоской фигуры (или траектории этих точек); мгновенный центр скоростей находится в точке пересечения перпендикуляров, восставленных из точек А и В к скоростям этих точек (или к касательным к траекториям).
каких-нибудь двух точек А и В плоской фигуры (или траектории этих точек); мгновенный центр скоростей находится в точке пересечения перпендикуляров, восставленных из точек А и В к скоростям этих точек (или к касательным к траекториям).
2) Для определения скорости любой точки плоской фигуры надо знать модуль и направление скорости какой-нибудь одной точки А фигуры и направление скорости другой ее точки В. Тогда, восстановив из точек А и В перпендикуляры к 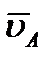 и
и 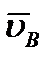 , построим мгновенный центр скоростей Р и по направлению
, построим мгновенный центр скоростей Р и по направлению 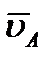 определим направление поворота фигуры. После этого, зная
определим направление поворота фигуры. После этого, зная 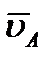 , найдем по формуле (2.42) скорость
, найдем по формуле (2.42) скорость 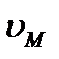 любой точки М плоской фигуры. Направлен вектор
любой точки М плоской фигуры. Направлен вектор 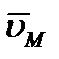 перпендикулярно РМ в сторону поворота фигуры.
перпендикулярно РМ в сторону поворота фигуры.
3) Угловая скорость плоской фигуры равна в каждый данный момент времени отношению скорости какой-нибудь точки фигуры к ее расстоянию от мгновенного центра скоростей Р:
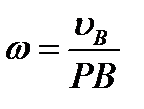
| (2.43) |
что видно из формул (2.41).
Рассмотрим некоторые частные случаи определения мгновенного центра скоростей.
а) Если плоскопараллельное движение осуществляется путем качения без скольжения одного цилиндрического тела по поверхности другого неподвижного, то точка Р катящегося тела, касающаяся неподвижной поверхности (рисунок 2_25),
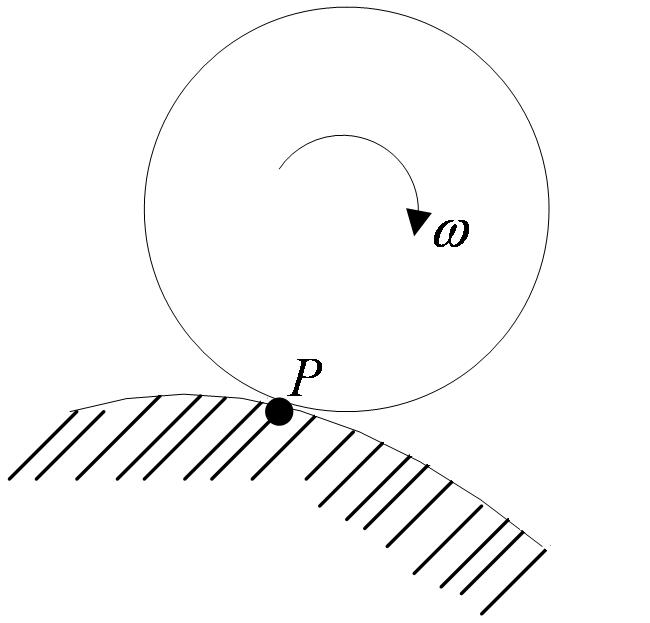
имеет в данный момент времени вследствие отсутствия скольжения скорость, равную нулю 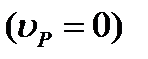 , и, следовательно, является мгновенным центром скоростей. Примером служит качение колеса по рельсу.
, и, следовательно, является мгновенным центром скоростей. Примером служит качение колеса по рельсу.
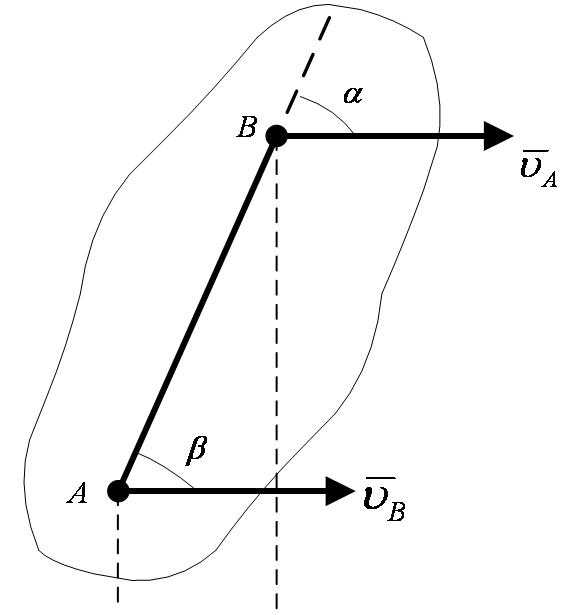
б) Если скорости точек А и В плоской фигуры параллельны друг другу, причем линия АВ не перпендикулярна 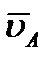 (рисунок 2_26),
(рисунок 2_26),
то мгновенный центр скоростей лежит в бесконечности и скорости всех точек параллельны 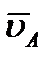 . При этом из теоремы о проекциях скоростей следует, что
. При этом из теоремы о проекциях скоростей следует, что 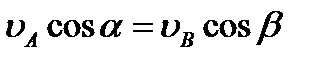 , т.е.
, т.е. 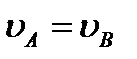 ; аналогичный результат получается для всех других точек. Следовательно, в рассматриваемом случае скорости всех точек фигуры в данный момент времени равны друг другу и по модулю, и по направлению, т.е. фигура имеет мгновенное поступательное распределение скоростей (такое состояние движения тела называют еще мгновенно поступательным). Угловая скорость ω тела в этот момент времени равна нулю.
; аналогичный результат получается для всех других точек. Следовательно, в рассматриваемом случае скорости всех точек фигуры в данный момент времени равны друг другу и по модулю, и по направлению, т.е. фигура имеет мгновенное поступательное распределение скоростей (такое состояние движения тела называют еще мгновенно поступательным). Угловая скорость ω тела в этот момент времени равна нулю.
в) Если скорости точек А и В плоской фигуры параллельны друг другу и при этом линия АВ перпендикулярна 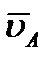 , то мгновенный центр скоростей Р определяется построением, показанным на рисунке 2_27.
, то мгновенный центр скоростей Р определяется построением, показанным на рисунке 2_27.
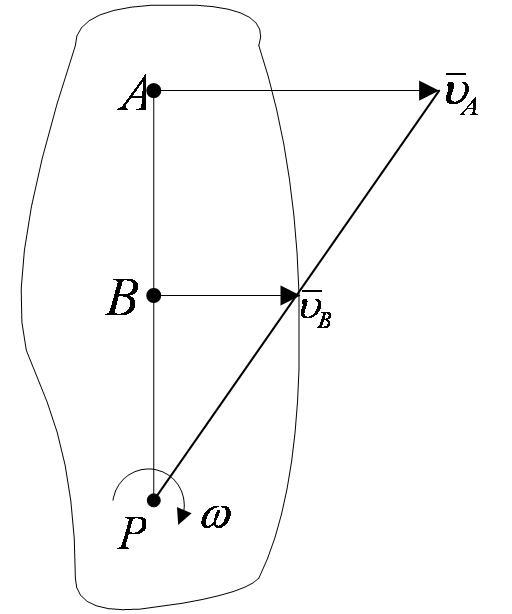
Справедливость построений следует из пропорции (2.42). В этом случае, в отличие от предыдущих, для нахождения центра P надо кроме направлений знать еще и модули скоростей 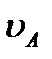 и
и 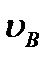 .
.
Определение ускорений точек плоской фигуры
Покажем, что ускорение любой точки М плоской фигуры (так же, как и скорость) складывается из ускорений, которые точка получает при поступательном и вращательном движениях этой фигуры. Положение точки М по отношению к осям Оху (рисунок 2_21)

определяется радиусом-вектором 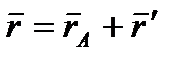 , где
, где 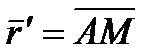 . Тогда
. Тогда 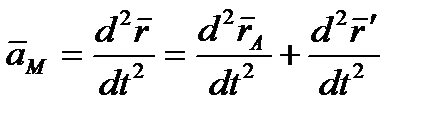 .
.
В правой части этого равенства первое слагаемое есть ускорение 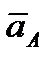 полюса А, а второе слагаемое определяет ускорение
полюса А, а второе слагаемое определяет ускорение 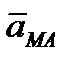 , которое точка М получает при вращении фигуры вокруг полюса А. Следовательно,
, которое точка М получает при вращении фигуры вокруг полюса А. Следовательно,
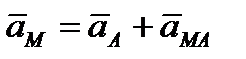
| (2.44) |
Значение 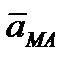 , как ускорения точки вращающегося твердого тела:
, как ускорения точки вращающегося твердого тела:
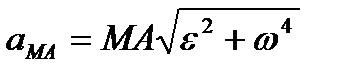 , , 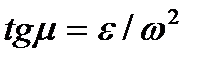 , ,
| (2.45) |
где ω и ε – угловая скорость и угловое ускорение фигуры, а μ – угол между вектором 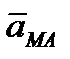 и отрезком МА.
и отрезком МА.
Таким образом, ускорение любой точки М плоской фигуры геометрически складывается из ускорения какой-нибудь другой точки А, принятой за полюс, и ускорения, которое точка М получает при вращении фигуры вокруг этого полюса. Модуль и направление ускорения 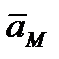 находятся построением соответствующего параллелограмма (рисунок 2_28).
находятся построением соответствующего параллелограмма (рисунок 2_28).
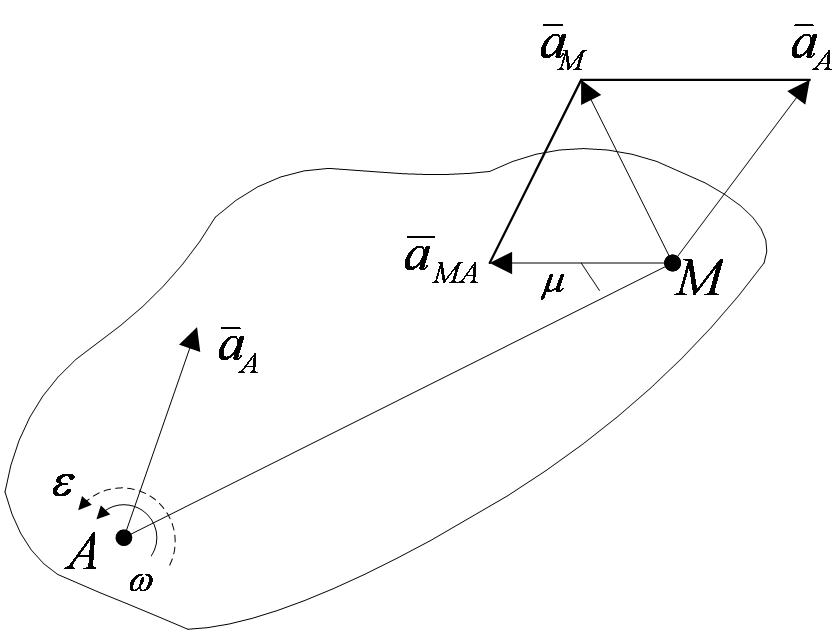
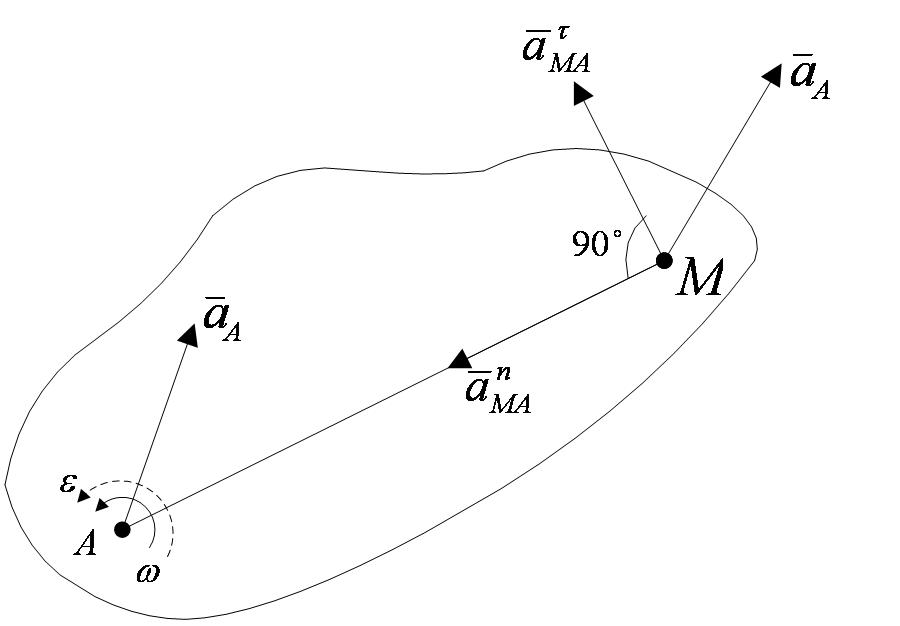
Однако вычисление 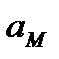 с помощью параллелограмма, изображенного на рисунке 2_28, усложняет расчет, так как предварительно надо будет находить значение угла μ, а затем – угла между векторами
с помощью параллелограмма, изображенного на рисунке 2_28, усложняет расчет, так как предварительно надо будет находить значение угла μ, а затем – угла между векторами 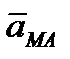 и
и 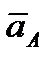 . Поэтому при решении задач удобнее вектор
. Поэтому при решении задач удобнее вектор 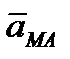 заменять его касательной
заменять его касательной 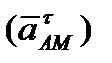 и нормальной
и нормальной 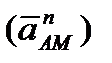 составляющими и представить равенство (2.44) в виде
составляющими и представить равенство (2.44) в виде
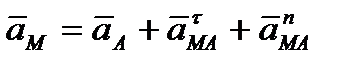
| (2.46) |
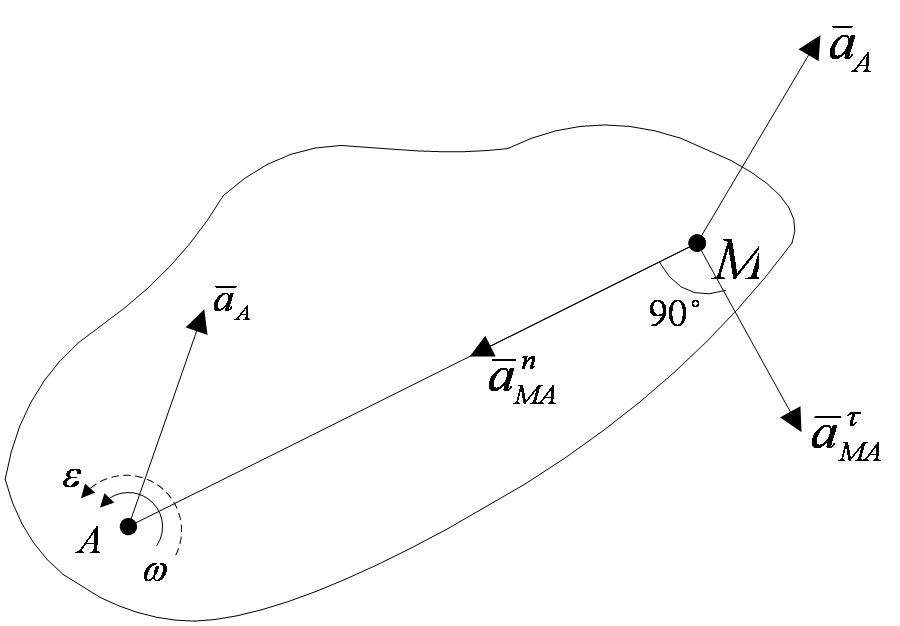
При этом вектор 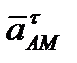 направлен перпендикулярно АМ в сторону вращения, если оно ускоренное (рисунок 2_29),
направлен перпендикулярно АМ в сторону вращения, если оно ускоренное (рисунок 2_29),
и против вращения, если оно замедленное; вектор 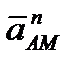 всегда направлен от точки М к полюсу А (рисунок 2_30).
всегда направлен от точки М к полюсу А (рисунок 2_30).
Численно же
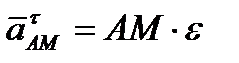 , , 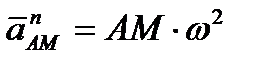 . .
| (2.47) |
Если полюс А движется не прямолинейно, то его ускорение можно тоже представить как сумму касательной 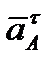 и нормальной
и нормальной 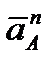 составляющих, тогда
составляющих, тогда
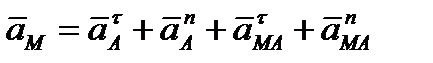
| (2.48) |
Наконец, когда точка М движется криволинейно и ее траектория известна, то 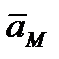 в левых частях равенств (2.46) и (2.48) можно заменить суммой
в левых частях равенств (2.46) и (2.48) можно заменить суммой 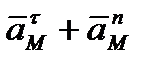 . Формулами (2.46-2.50) и пользуются обычно при решении задач.
. Формулами (2.46-2.50) и пользуются обычно при решении задач.
Мгновенный центр ускорений.
Термин мгновенный центр ускорений. Определяется положение мгновенного центра ускорений Q, если известны ускорение 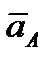 какой-нибудь точки А фигуры и величины ω и ε, следующим путем:
какой-нибудь точки А фигуры и величины ω и ε, следующим путем:
1) находим значение угла μ из формулы 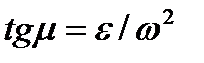 ;
;
2) от точки А под углом μ к вектору 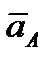 проводим прямую АЕ (рисунок 2_31);
проводим прямую АЕ (рисунок 2_31);
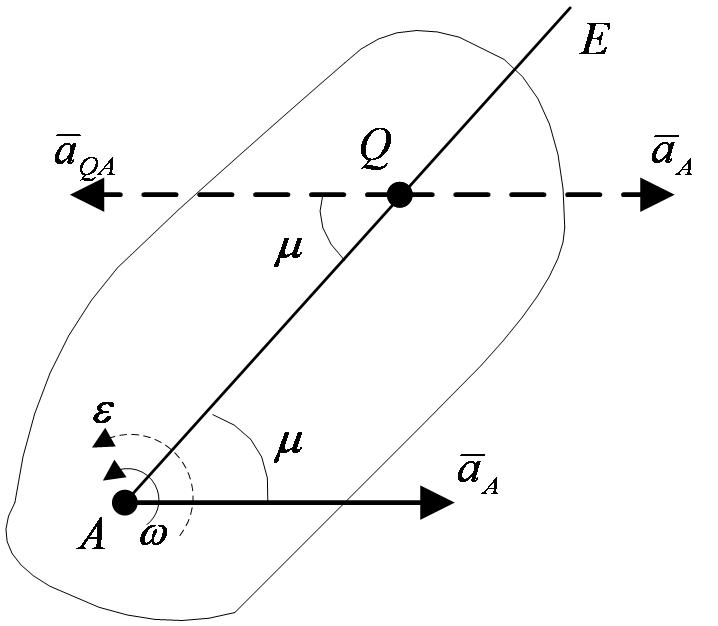
при этом прямая АЕ должна быть отклонена от 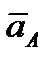 в сторону вращения фигуры, если вращение является ускоренным, и против вращения, если оно является замедленным, т. е. в сторону направления углового ускорения ε;
в сторону вращения фигуры, если вращение является ускоренным, и против вращения, если оно является замедленным, т. е. в сторону направления углового ускорения ε;
3) откладываем вдоль линии АЕ отрезок AQ, равный
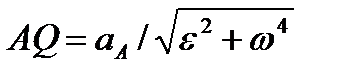
| (2.49) |
Построенная таким путем точка Q и будет мгновенным центром ускорений. В самом деле, по формулам (2.44) и (2.45) 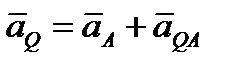 ,где численно
,где численно 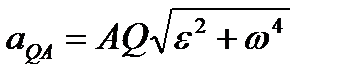 . Подставляя сюда значение AQ из равенства (2.49), находим, что
. Подставляя сюда значение AQ из равенства (2.49), находим, что 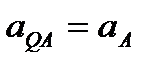 . Кроме того, вектор
. Кроме того, вектор 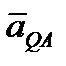 должен образовывать с линией AQ угол μ, следовательно, вектор
должен образовывать с линией AQ угол μ, следовательно, вектор 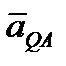 параллелен
параллелен 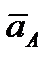 , но направлен в противоположную сторону. Поэтому
, но направлен в противоположную сторону. Поэтому 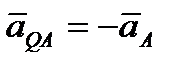 и
и 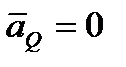 .
.
Если точку Q выбрать за полюс, то так как 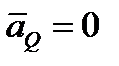 , ускорение любой точки М тела, согласно формуле (2.44) будет
, ускорение любой точки М тела, согласно формуле (2.44) будет
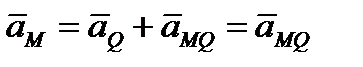
| (2.50) |
При этом из равенств (2.45) следует, что численно
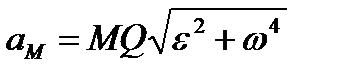
| (2.51) |
Следовательно, ускорения точек плоской фигуры определяются в данный момент времени так, как если бы движение фигуры было вращением вокруг мгновенного центра ускорений Q. При этом, как следует из (2.51),
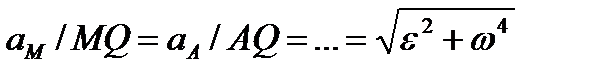
| (2.52) |
т. е. ускорения точек плоской фигуры пропорциональны их расстояниям от мгновенного центра ускорений.
Раздел 3 ДИНАМИКА
Лекция №7 Тема 3.1 Динамика свободной материальной точки.
Вопросы:
3.1.1.Введение в динамику. Предмет динамики. Динамика точки. Основные понятия и определения. Законы динамики.
3.1.2. Дифференциальные уравнения движения свободной материальной точки. Векторное уравнение движения. Уравнения движения в декартовой системе координат. Уравнения движения в естественном виде.
3.1.3. Две основные задачи динамики. Решение первой задачи. Вторая задача динамики. Интегрирование дифференциальных уравнений движения в простейших случаях.
В основе динамики лежат законы, установленные путем обобщений результатов целого ряда опытов и наблюдений, посвященных изучению движения тел, и проверенные обширной общественно-производственной практикой человечества. Систематически законы динамики были впервые изложены И. Ньютоном в его классическом сочинении «Математические начала натуральной философии», изданном в 1687 г. Сформулировать эти законы можно следующим образом.
Первый Закон (закон инерции):
Изолированная от внешних воздействий материальная точка сохраняет свое состояние покоя или равномерного прямолинейного движения до тех пор, пока приложенные силы не заставят ее изменить это состояние.
Термин движение по инерции.
Закон инерции отражает одно из основных свойств материи – пребывать неизменно в движении. Важно отметить, что развитие динамики как науки стало возможным лишь после того, как Галилеем был открыт этот закон (1638 г.) и тем самым опровергнута господствовавшая со времен Аристотеля точка зрения о том, что движение тела может происходить только под действием силы.
Второй закон (основной закон динамики) устанавливает, как изменяется скорость точки, при действии на нее какой-нибудь силы, а именно:
Произведение массы материальной точки на ускорение, которое она получает под действием данной силы, равно по модулю этой силе, а направление ускорения совпадает с направлением силы.
Математически этот закон выражается векторным равенством
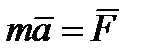
| (3.1) |
При этом между модулями ускорения и силы имеет место зависимость 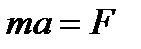 .
.
Если на точку действует одновременно несколько сил, то она, как это следует из закона параллелограмма сил, будут эквивалентны одной силе, т.е. равнодействующей 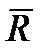 , равной геометрической сумме данных сил. Уравнение, выражающее основной закон динамики, принимает в этом случае вид
, равной геометрической сумме данных сил. Уравнение, выражающее основной закон динамики, принимает в этом случае вид
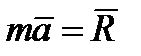 или или 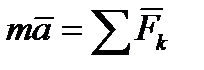 . .
| (3.2) |
Третий закон (закон равенства действия и противодействия) устанавливает характер механического взаимодействия между материальными телами. Для двух, материальных точек он гласит:
Две материальные точки действуют друг на друга с силами, равными по модулю и направленными вдоль прямой, соединяющей эти точки, в противоположные стороны.
Этим законом мы уже пользовались в статике. Он играет большую роль в динамике системы материальных точек, как устанавливающий зависимость между действующими на эти точки внутренними силами.
При взаимодействии двух свободных материальных точек, они, согласно третьему и второму законам динамики, будут двигаться с ускорениями, обратно пропорциональными их массам.
Для свободной материальной точки задачами динамики являются следующие: 1) зная закон движения точки, определить действующую на нее силу (первая задача динамики); 2) зная действующие на точку силы, определить закон движения точки (вторая, или основная, задача динамики).
Основные виды сил
При решении задач динамики мы будем в основном рассматривать следующие постоянные или переменные силы:
Сила тяжести. Это постоянная сила Р, действующая на любое тело, находящееся вблизи земной поверхности. Модуль силы тяжести равен весу тела.
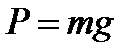 или или 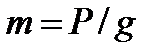 . .
| (3.3) |
Сила трения. Так будем кратко называть силу трения скольжения, действующую (при отсутствии жидкой смазки) на движущееся тело. Ее модуль определяется равенством
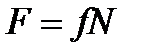 , ,
| (3.4) |
где 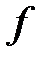 – коэффициент трения, который будем считать постоянным; N – нормальная реакция.
– коэффициент трения, который будем считать постоянным; N – нормальная реакция.
Сила тяготения. Это сила, с которой два материальных тела притягиваются друг к другу по закону всемирного тяготения, открытому Ньютоном. Сила тяготения зависит от расстояния и для двух материальных точек с массами 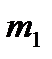 и
и 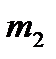 , находящихся на расстоянии
, находящихся на расстоянии 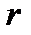 друг от друга, выражается равенством
друг от друга, выражается равенством
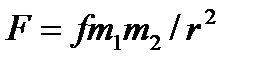
| (3.5) |
где 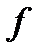 – гравитационная постоянная (в СИ
– гравитационная постоянная (в СИ 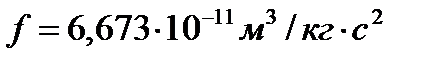 ).
).
Сила упругости. Эта сила тоже зависит от расстояния. Ее значение можно определить исходя из закона Гука, согласно которому напряжение (сила, отнесенная к единице площади) пропорционально деформации. В частности, для силы упругости пружины получается значение
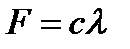
| (3.6) |
где 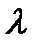 – удлинение (или сжатие) пружины;
– удлинение (или сжатие) пружины;  – так называемый коэффициент жесткости пружины (в СИ измеряется в Н/м).
– так называемый коэффициент жесткости пружины (в СИ измеряется в Н/м).
Сила вязкого трения. Такая сила, зависящая от скорости, действует на тело при его медленном движении в очень вязкой среде (или при наличии жидкой смазки) и может быть выражена равенством
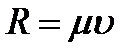
| (3.7) |
где 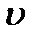 – скорость тела;
– скорость тела; 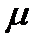 – коэффициент сопротивления.
– коэффициент сопротивления.
Сила аэродинамического (гидродинамического) сопротивления. Эта сила тоже зависит от скорости и действует на тело, движущееся в такой, например, среде, как воздух или вода. Обычно ее величину выражают равенством
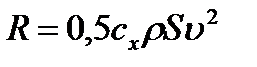
| (3.8) |
где 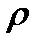 – плотность среды;
– плотность среды; 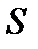 – площадь проекции тела на плоскость, перпендикулярную направлению движения (площадь миделя);
– площадь проекции тела на плоскость, перпендикулярную направлению движения (площадь миделя); 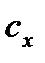 – безразмерный коэффициент сопротивления, определяемый обычно экспериментально и зависящий от формы тела и от того, как оно ориентировано при движении.
– безразмерный коэффициент сопротивления, определяемый обычно экспериментально и зависящий от формы тела и от того, как оно ориентировано при движении.
Для решения задач динамики точки будем пользоваться одной из следующих двух систем уравнений:
Уравнения в декартовых координатах.
Из кинематики известно, что движение точки в прямоугольных декартовых координатах задается уравнениями: 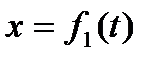 ,
, 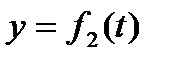 ,
, 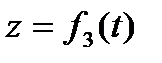 .
.
Задачи динамики точки состоят в том, чтобы, зная движение точки, т, определить действующую на точку силу или, наоборот, зная действующие на точку силы, определить закон ее движения. Следовательно, для решения задач динамики точки надо иметь уравнения, связывающие координаты х, у, z этой точки и действующую на нее силу (или силы). Эти уравнения и дает второй закон динамики.
Рассмотрим материальную точку, движущуюся под действием сил 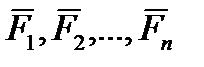 по отношению к инерциальной системе отсчета Оxyz. Проектируя обе части равенства
по отношению к инерциальной системе отсчета Оxyz. Проектируя обе части равенства 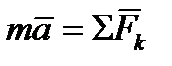 , на оси х, у, z и учитывая, что
, на оси х, у, z и учитывая, что 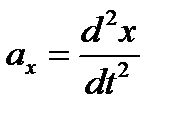 и т. д., получим:
и т. д., получим:
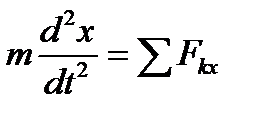 ; ; 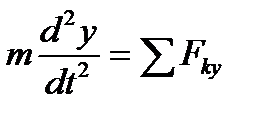 ; ; 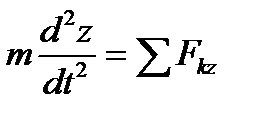
| (3.9) |
или, обозначая вторые производные по времени двумя точками,
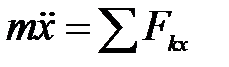 ; ; 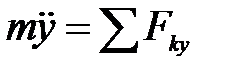 ; ; 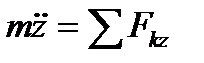
| (3.9') |
Это и будут искомые уравнения, т. е. дифференциальные уравнения движения точки в прямоугольных декартовых координатах.
Так как действующие силы могут зависеть от времени t, от положения точки, т. е. от ее координат х, у, z, и от скорости, т. е. от 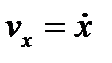 ,
, 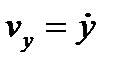 ,
, 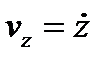 , то в общем случае правая часть каждого из уравнений (3.9) может быть функцией всех этих переменных, т. е. t, x, у, z,
, то в общем случае правая часть каждого из уравнений (3.9) может быть функцией всех этих переменных, т. е. t, x, у, z, 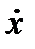 ,
, 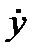 ,
, 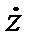 одновременно.
одновременно.
Уравнения в проекциях на оси естественного трехгранника.
Для получения этих уравнений спроектируем обе части равенства 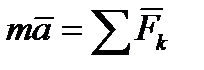 на оси
на оси 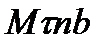 , т. е. на касательную
, т. е. на касательную 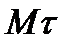 к траектории точки, главную нормаль
к траектории точки, главную нормаль 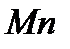 , направленную в сторону вогнутости траектории, и бинормаль
, направленную в сторону вогнутости траектории, и бинормаль 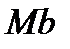 . Тогда, учитывая, что
. Тогда, учитывая, что 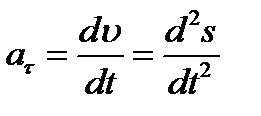 ,
, 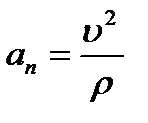 ,
, 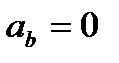 получим
получим
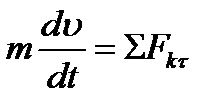 , , 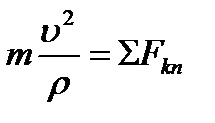 , , 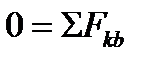
| (3.10) |
Решение первой задачи динамики
Если ускорение движущейся точки задано, то действующая сила или реакция связи сразу находится по уравнениям (3.1) или (3.2). При этом для вычисления реакции надо дополнительно знать активные силы. Когда ускорение непосредственно не задано, но известен закон движения точки, то для определения силы можно воспользоваться уравнениями (3.9) или (3.10).
Решение основной задачи динамики при прямолинейном движении точки
Движение материальной точки будет прямолинейным, когда действующая на нее сила (или равнодействующая приложенных сил) имеет постоянное направление, а скорость точки в начальный момент времени равна нулю или направлена вдоль силы.
Если при прямолинейном движении направить вдоль траектории координатную ось Ох, то движение точки будет определяться первым из уравнений движения точки в прямоугольных декартовых координатах, т. е. уравнением
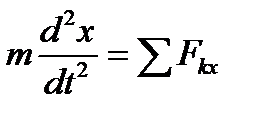 или или 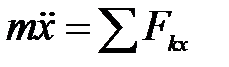
| (3.11) |
Уравнение (3.11) называют дифференциальным уравнением прямолинейного движения точки. Иногда его удобнее заменить двумя уравнениями, содержащими первые производные:
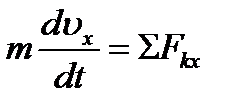 , , 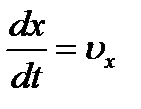 . .
| (3.12) |
В случаях, когда при решении задачи надо искать зависимость скорости от координаты х, а не от времени t (или когда сами силы зависят от х), уравнение (3.12) преобразуют к переменному х. Так как 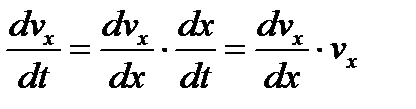 , то вместо (3.12) получим:
, то вместо (3.12) получим:
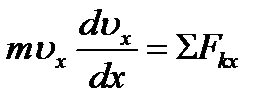 , , 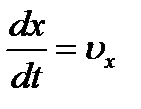
| (3.13) |
Решение основной задачи динамики сводится к тому, чтобы из данных уравнений, зная силы, найти закон движения точки, т. е. x=f(t). Для этого надо проинтегрировать соответствующее дифференциальное уравнение.
Чтобы яснее было, к чему сводится эта математическая задача, вспомним, что входящие в правую часть уравнения (3.11) силы могут зависеть от времени t, от положения точки, т. е. от х, и от ее скорости, т.е. от 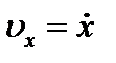 . Следовательно, в общем случае уравнение (3.11) с математической точки зрения представляет собой дифференциальное уравнение второго порядка, имеющее вид
. Следовательно, в общем случае уравнение (3.11) с математической точки зрения представляет собой дифференциальное уравнение второго порядка, имеющее вид 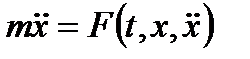 .
.
Если для данной конкретной задачи дифференциальное уравнение (3.11) будет проинтегрировано, то в полученное решение войдут две постоянные интегрирования C1 и С2 и общее решение уравнения (3.11) будет иметь вид
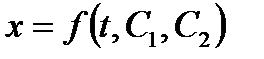 . .
| (3.14) |
Чтобы довести решение каждой конкретной задачи до конца, надо определить значения постоянных C1 и С2. Для этого используются обычно так называемые начальные условия.
Изучение всякого движения будем начинать с некоторого определенного момента времени, называемого начальным моментом. От этого момента будем отсчитывать время движения, считая, что в начальный момент t=0. Обычно за начальный принимают момент начала движения под действием заданных сил. Положение, которое точка занимает в начальный момент, называется начальным положением, а ее скорость в этот момент – начальной скоростью. Чтобы решить основную задачу динамики, надо кроме действующих сил знать еще начальные условия, т. е. положение и скорость точки в начальный момент времени.
В случае прямолинейного движения начальные условия задаются в виде
при 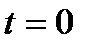 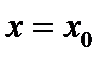 , , 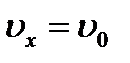 . .
| (3.15) |
По начальным условиям можно определить конкретные значения постоянных C1 и С2 и найти частное решение уравнения (3.11), дающее закон движения точки, в виде
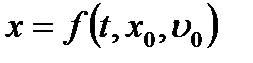 . .
| (3.16) |
Дата добавления: 2021-06-28; просмотров: 499;











