Лекция №3 Тема 1.3 Условия равновесия свободного абсолютно твердого тела

Вопросы:

1.3.1. Система сил, произвольно расположенных на плоскости. Приведение сил к центру. Главный вектор и главный момент, их вычисление.

1.3.2. Векторные и аналитические условия и уравнения равновесия произвольной пространственной системы сил, произвольной плоской и системы параллельных сил. Возможные случаи приведения произвольной системы сил.

1.3.3.Теорема Вариньона о моменте равнодействующей. Инварианты статики. Равновесие сочлененной системы тел.

1.3.4.Центр параллельных сил и центр тяжести тела. Формулы для определения координат центра параллельных сил. Центр тяжести твердого тела, формулы для определения его координат. Координаты центра тяжести одного тела. Способы определения положения центров тяжести тел.

Теорема о параллельном переносе силы

Равнодействующая системы сходящихся сил непосредственно находится с помощью закона параллелограмма сил. Очевидно, что аналогичную задачу можно будет решить и для произвольной системы сил, если найти для них метод, позволяющий перенести все силы в одну точку. Такой метод дает следующая теорема: силу, приложенную к абсолютно твердому телу, можно, не изменяя оказываемого ею действия, переносить из данной точки в любую другую точку тела, прибавляя при этом пару с моментом, равным моменту переносимой силы относительно точки, куда сила переносится.

Пусть на твердое тело действует сила F, приложенная в точке А (рисунок 1_27).

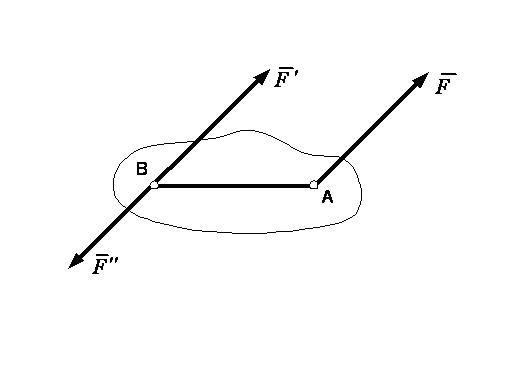
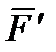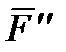Действие этой силы не изменяется, если в любой точке В тела приложить две уравновешенные силы и , такие, что 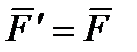, 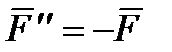. Полученная система трех сил и представляет собой силу 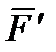, равную 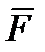, но приложенную в точке В, и пару 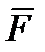, 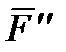с моментом

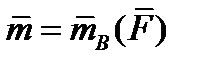
(1.15)

Таким образом, теорема доказана. Результат, даваемый теоремой, можно еще изобразить так, как это показано на рисунке 1_28 (силу 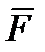на этом рисунке надо считать отброшенной).

Приведение системы сил к данному центру

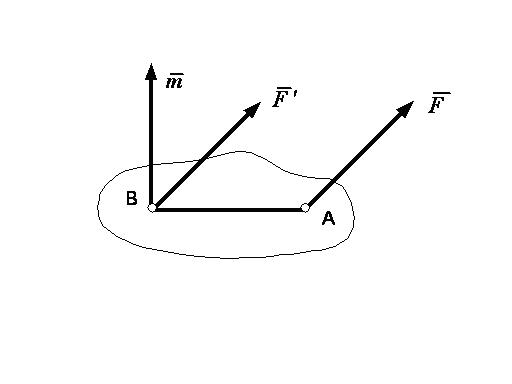
Решим теперь задачу о приведении произвольной системы сил к данному центру, т. е. о замене данной системы сил другой, ей эквивалентной, но значительно более простой, а именно состоящей, как мы увидим, только из одной силы и пары.

Пусть на твердое тело действует произвольная система сил 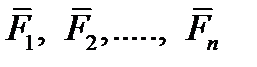(рисунок 1_29).

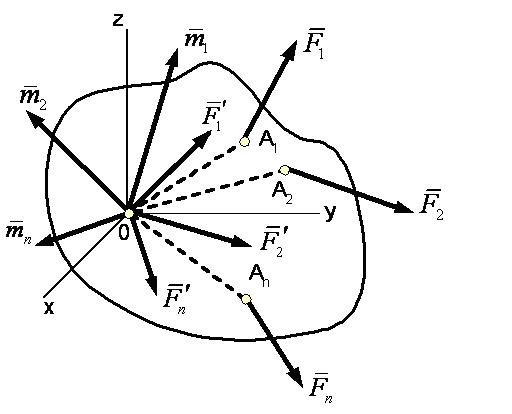
Выберем какую-нибудь точку О за центр приведения и, пользуясь теоремой, перенесем все силы в центр О, присоединяя при этом соответствующие пары (см. рисунок 1_28).

Тогда на тело будет действовать система сил

(1.16)

приложенных в центре О, и система пар, моменты которых согласно формуле (1.15) равны:

(1.17)

Сходящиеся силы, приложенные в точке О, заменяются одной силой 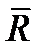, приложенной в точке О, При этом 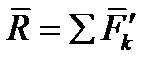или, согласно равенствам (1.16),

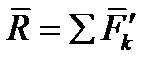
(1.18)

Чтобы сложить все полученные пары, надо сложить векторы моментов этих пар. В результате система пар заменится одной парой, момент которой 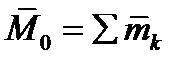или, согласно равенствам (1.17),

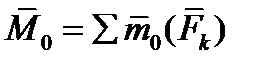
(1.19)

Как известно, величина 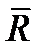, равная геометрической сумме всех сил, называется главным вектором системы сил; величина 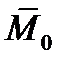, равная геометрической сумме моментов всех сил относительно центра О, называется главным моментом системы сил относительно этого центра.

Таким образом, мы доказали следующую теорему о приведении системы сил: любая система сил, действующих на абсолютно твердое тело, при приведении к произвольно выбранному центру О заменяется одной силой 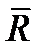, равной главному вектору системы сил и приложенной в центре приведения О, и одной парой с моментом 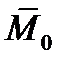, равным главному моменту системы сил относительно центра О (рисунок 1_30).

Заметим, что сила 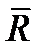не является здесь равнодействующей данной системы сил, так как заменяет систему сил не одна, а вместе с парой.

Из доказанной теоремы следует, что две системы сил, имеющие одинаковые главные векторы и главные моменты относительно одного и того же центра, эквивалентны (условия эквивалентности систем сил).

Отметим еще, что значение 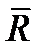от выбора центра О, очевидно, не зависит. Значение же 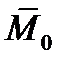при изменении положения центра О может в общем случае изменяться вследствие изменения значений моментов отдельных сил. Поэтому всегда необходимо указывать, относительно какого центра определяется главный момент.

Условия равновесия системы сил. Теорема о моменте равнодействующей

Покажем, что для равновесия любой системы сил необходимо и достаточно, чтобы главный вектор этой системы сил и ее главный момент относительно любого центра были равны нулю, т. е. чтобы выполнялись условия

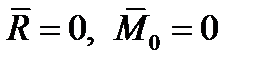
(1.20)

где О – любой центр, так как при 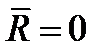значение 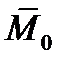от выбора центра О не зависит.

Условия (1.20) являются необходимыми, так как если какое-нибудь из них не выполняется, то система действующих на тело сил приводится или к равнодействующей (когда 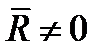), или к паре сил (когда 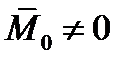) и, следовательно, не является уравновешенной. Одновременно условия (1.20) являются и достаточными, потому что при 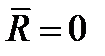система сил может приводиться только к паре с моментом 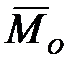, а так как 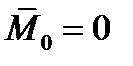, то имеет место равновесие.

Пользуясь полученным результатом, докажем следующую теорему Вариньона о моменте равнодействующей: если данная система сил имеет равнодействующую, то момент равнодействующей относительно любого центра О равен сумме моментов сил системы относительно того же центра.

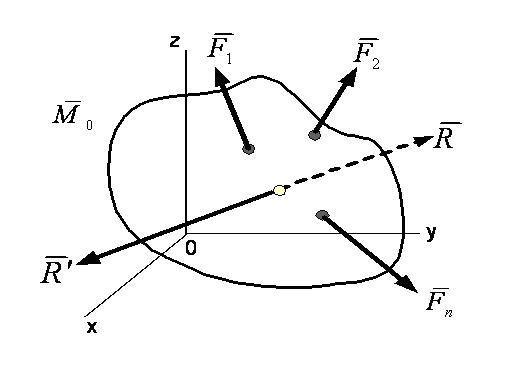
Пусть система сил 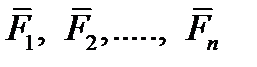приводится к равнодействующей 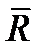, линия действия которой проходит через некоторую точку С (рисунок 1_31).

Приложим в этой точке силу 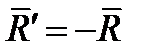. Тогда система сил 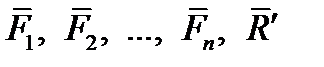будет находиться в равновесии и для нее должно выполняться условие 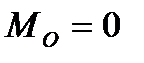, т.е. согласно формуле (1.19) для данных сил (включая силу 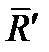) должно быть Но так как 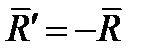и обе силы направлены вдоль одной и той же прямой, то 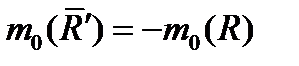Подставляя это значение 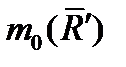в предыдущее равенство, найдем из него, что

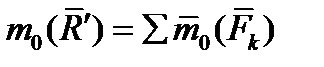
(1.21)

Тем самым теорема доказана. Ею часто бывает удобно пользоваться при вычислении моментов сил.