Лекция №8 Тема 3.2. Основные теоремы динамики материальной точки

Вопросы:

3.2.1. Количество движения и импульс силы. Теорема об изменении количества движения. Момент количества движения и теорема об изменении момента количества движения.

3.2.2. Элементарная и полная работа силы. Теорема о работе равнодействующей. Вычисление работы в частных случаях. Работа постоянной силы. Элементарная работа силы и ее аналитическое выражение. Работа сил тяжести и силы упругости. Работа силы, приложенной к вращающемуся телу.

3.2.3. Мощность. Кинетическая энергия и теорема об изменении кинетической энергии.

3.2.4. Принцип Даламбера для материальной точки и несвободной механической системы. Приведение сил инерции точек твердого тела к центру. Главный вектор и главный момент сил инерции. Приведение сил инерции при поступательном движении тела, вращении вокруг неподвижной оси и плоскопараллельном движении.

Одной из основных динамических характеристик движения точки является количество движения.

Термин количество движения. Направлен вектор 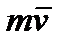так же, как и скорость точки, т. е. по касательной к ее траектории.

Единицей измерения количества движения является в СИ – 1 кг·м/с=1 Н·с.

Для характеристики действия, оказываемого на тело силой за некоторый промежуток времени, вводится понятие об импульсе силы.

Сначала введем понятие об элементарном импульсе, т. е. об импульсе за элементарный промежуток времени dt.

Термин элементарный импульс силы. Равен элементарный импульс

.

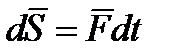(3.17)

Направлен элементарный импульс вдоль линии действия силы. Импульс 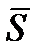любой силы 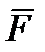за конечный промежуток времени 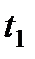вычисляется как предел интегральной суммы соответствующих элементарных импульсов, т. е.

.

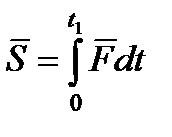(3.18)

Следовательно, импульс силы за некоторый промежуток времени 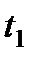равен определенному интегралу от элементарного импульса, взятому в пределах от нуля до .

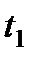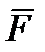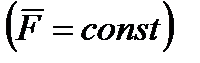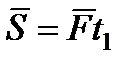В частном случае, если сила постоянна и по модулю, и по направлению , то . Причем в этом случае и модуль 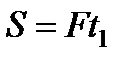. В общем случае модуль импульса может быть вычислен по его проекциям на координатные оси:

.

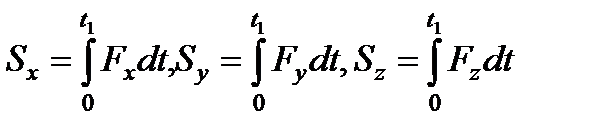(3.19)

Единицей измерения импульса силы, как и количества движения, является в СИ – 1 кг·м/с.

Теорема об изменении количества движения точки

Так как масса точки постоянна, а ее ускорение 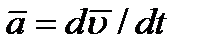, то уравнение 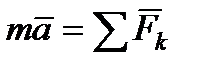выражающее основной закон динамики, можно представить в виде

.

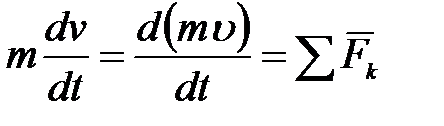(3.20)

Уравнение (3.20) выражает одновременно теорему об изменении количества движения точки в дифференциальной форме: производная по времени от количества движения точки равна сумме действующих на точку сил.

Пусть движущаяся точка имеет в момент времени t=0 скорость 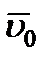, а в момент 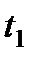– скорость 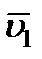. Умножим тогда обе части равенства (3.20) на dt и возьмем от них определенные интегралы. При этом справа, где интегрирование идет по времени, пределами интеграла будут 0 и 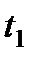, а слева, где интегрируется скорость, пределами интеграла будут соответствующие значения скорост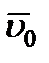и и 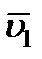. В результате получим:

.

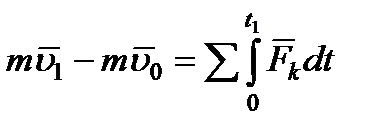Стоящие справа интегралы представляют собой импульсы действующих сил. Поэтому окончательно будет

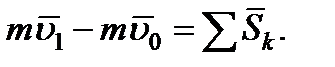
(3.21)

Уравнение (3.211) выражает теорему об изменении количества движения точки в конечном виде:

изменение количества движения точки за некоторый промежуток времени равно сумме импульсов всех действующих на точку сил за тот же промежуток времени.

При решении задач вместо векторного уравнения (3.21) часто пользуются уравнениями в проекциях. Проектируя обе части равенства (3.21) на координатные оси, получим

.

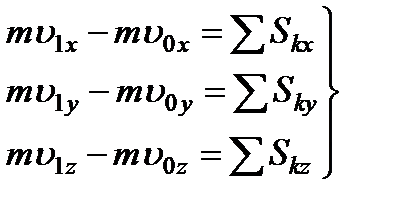(3.22)

В случае прямолинейного движения, происходящего вдоль оси Ох, теорема выражается первым из этих уравнений.