I. Математические понятия

1. Что составляет объём понятия «четырёхугольник»?

2. Что составляет содержание понятия «четырёхугольник»?

3. Посредством чего раскрывается объём и содержание понятия?

4. Перечислите виды определений.

Назовите виды следующих определений.

1) Квадратным корнем из числа а называется число, квадрат которого равен а.

2) Трапецией называется четырёхугольник, у которого только две противоположные стороны параллельны.

3) Пусть О – фиксированная точка и Х – произвольная точка плоскости. Отложим на продолжении отрезка ОХ за точку О отрезок ОХ¢, равный ОХ. Точка Х¢ называется симметричной точке Х относительно точки О.

4)Функция называется чётной, если для любого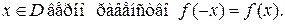

5. В чём состоит роль определений?

6. Как распознать трапецию?

7. Какие методы формирования понятий Вам известны?

8. Опишите любой метод формирования понятия.

II. Теоремы

1. Теорема – это …

2. Укажите вид формулировки теоремы.

1) В параллелограмме диагонали пересекаются и точкой пересечения делятся пополам.

2) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.

Следует ли учить школьников формулировать теорему в разных видах и почему?

3. Для теоремы «Сумма смежных углов равна 180°» сформулируйте обратное утверждение, противоположное и противоположное обратному. Как связана между собой истинность этих утверждений?

4. Представим теорему в виде «Если Р(х)ÞQ(х)».

Q(х) – это…

Р(х) – это …

Сформулируйте теорему из пункта (3) в терминах “необходимо” и ”достаточно”.

5.При каком условии необходимость является достаточностью?

6. Продолжите запись.

Для того чтобы четырехугольник был параллелограммом необходимо и достаточно, чтобы его противоположные стороны были равны.

Необходимость. Достаточность.

Дано: Дано:

Доказать: Доказать:

7. Охарактеризуйте этапы работы над теоремой до её доказательства.

III. Задачи

1. Какова роль задач в обучении?

2. Определите роль следующих задач.

№1. Два мальчика купили бананы. Один сказал другому: «Дай мне два твоих банана и у нас будет поровну». Другой ответил: «Дай мне два твоих банана и у меня будет в два раза больше, чем у тебя». Сколько бананов было у каждого?

№2. Мотоциклист ехал из одного города в другой 4 часа. На обратном пути первые 100 км он ехал с той же скоростью, а затем уменьшил её на 10 км/ч и поэтому на обратный путь затратил на 30 мин больше. Найти расстояние между городами.

№3. Желая доказать, что гипотенуза прямоугольного треугольника больше катета, ученик провел из вершины прямого угла А треугольника АВС такой луч АМ (М – на гипотенузе ВС), что ÐВАМ=0,5ÐС (рис 1). Как он собирался решать задачу?

3.Каковы функции задач в процессе обучения математике?

4.Приведите пример задачи и укажите её функцию.

5.Перечислите этапы решения задачи.

IV. Методы

1. Приведите классификацию методов обучения математике.

2. Перечислите научные методы. Почему они так называются?

3. Какой метод используется при введении распределительного закона умножения в 5 классе? В чём суть этого метода? Как он реализуется?

4. Какие виды анализа используются в обучении математике?

6. При исследовании функции и построении её графика какой вид анализа применяется?

7. В чём разница между нисходящим и восходящим анализом?

8. На примере задачи о произведении отрезков хорд проиллюстрируйте поиск решения методом восходящего анализа.