Лекция № 5 Тема 2.2 Кинематика простейших движений абсолютно твердого тела
Вопросы:
2.2.1. Поступательное движение твердого тела. Теорема о траекториях точек тела. Теорема о распределении скоростей и ускорений. Уравнения поступательного движения.
2.2.2. Вращательное движение тела вокруг оси. Угловая скорость и угловое ускорение. Линейная скорость и линейное ускорение точки тела. Распределение линейных скоростей и ускорений точек тела, вращающегося вокруг неподвижной оси.
В кинематике, как и в статике, будем рассматривать всё твердые тела как абсолютно твердые. Задачи кинематики твердого тела распадаются на две части:
1) задание движения и определение кинематических характеристик движения тела в целом;
2) определение кинематических характеристик движения отдельных точек тела.
Начнем с рассмотрения поступательного движения твёрдого тела.
Термин поступательное движение.
Поступательное движение не следует смешивать с прямолинейным. При поступательном движении тела траектории его точек могут быть любыми кривыми линиями.
Приведем примеры.
1. Кузов автомобиля на прямом горизонтальном участке дороги движется поступательно. При этом траектории его точек будут прямыми линиями.
2. Спарник АВ (рисунок 2_11)
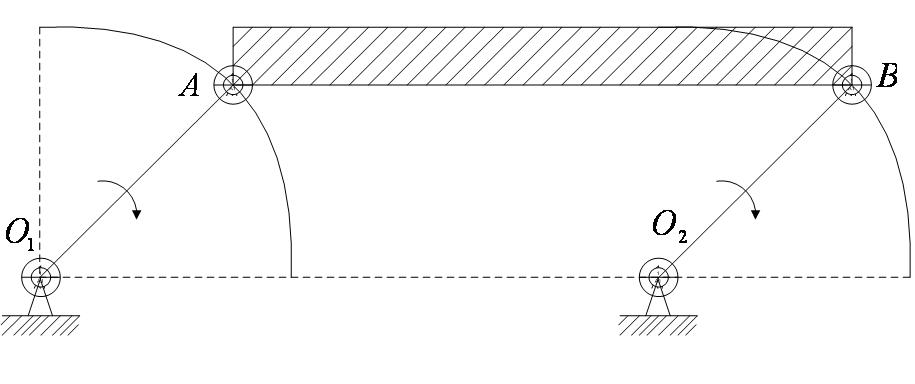
при вращении кривошипов 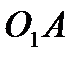 и
и 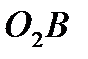 (
(  ) также движется поступательно (любая проведенная в нем прямая остается параллельной ее начальному направлению). Точки спарника движутся при этом по окружностям.
) также движется поступательно (любая проведенная в нем прямая остается параллельной ее начальному направлению). Точки спарника движутся при этом по окружностям.
Свойства поступательного движения определяются следующей теоремой: при поступательном движении все точки тела описывают одинаковые (при наложении совпадающие) траектории и имеют в каждый момент времени одинаковые по модулю и направлению скорости и ускорения.
Для доказательства рассмотрим твердое тело, совершающее поступательное движение относительно системы отсчета Охуz. Возьмем в теле две произвольные точки A и В, положения которых в момент времени 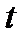 определяются радиусами-векторами
определяются радиусами-векторами 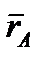 и
и  (рисунок 2_12);
(рисунок 2_12);
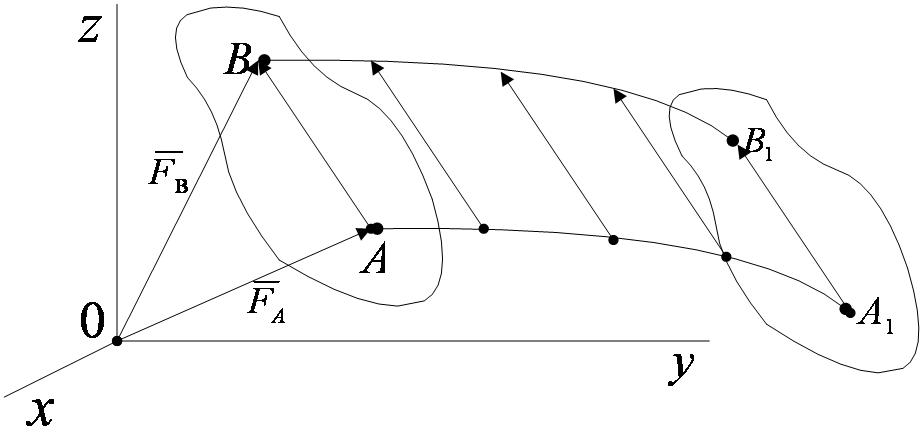
проведем вектор 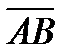 соединяющий эти точки. Тогда
соединяющий эти точки. Тогда
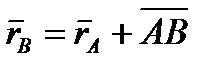
| (2.24) |
При этом длина АВ постоянна, как расстояние между точками твердого тела, а направление АВ остается неизменным, так как тело движется поступательно. Таким образом, вектор АВ во все время движения тела остается постоянным 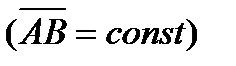 . Вследствие этого как видно из равенства (2.24) (и непосредственно из чертежа), траектория точки В получается из траектории точки А параллельным смещением всех ее точек на постоянный вектор
. Вследствие этого как видно из равенства (2.24) (и непосредственно из чертежа), траектория точки В получается из траектории точки А параллельным смещением всех ее точек на постоянный вектор 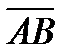 . Следовательно, траектории точек А и В будут действительно одинаковыми (при наложении совпадающими) кривыми.
. Следовательно, траектории точек А и В будут действительно одинаковыми (при наложении совпадающими) кривыми.
Для нахождения скоростей точек А и В продифференцируем обе части равенства (2.24) по времени. Получим 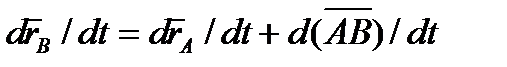 .
.
Но производная от постоянного вектора АВ равна нулю. Производные же от векторов 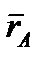 и
и 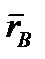 по времени дают скорости, точек А и B. В результате находим, что
по времени дают скорости, точек А и B. В результате находим, что 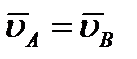 , т.е. что скорости точек A и В тела в любой момент времени одинаковы и по модулю, и по направлению. Беря от обеих частей полученного равенства производные по времени, найдём:
, т.е. что скорости точек A и В тела в любой момент времени одинаковы и по модулю, и по направлению. Беря от обеих частей полученного равенства производные по времени, найдём: 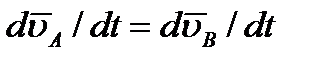 или
или 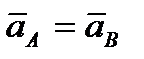 .
.
Следовательно, ускорения точек А и В тела в любой момент времени тоже одинаковы по модулю и направлению.
Так как точки А и В были выбраны произвольно, то из найденных результатов следует, что у всех точек тела их траектории, а также скорости и ускорения в любой момент времени будут одинаковы. Таким образом, теорема доказана.
Из теоремы следует, что поступательное движение твердого тела вполне определяется движением какой-нибудь одной его точки. Следовательно, изучение поступательного движения тела сводится к задаче кинематики точки, нами уже рассмотренной.
Вращательное движение твердого тела вокруг оси. Угловая скорость и угловое ускорение
Термин вращательное движение (рисунок 2_13).
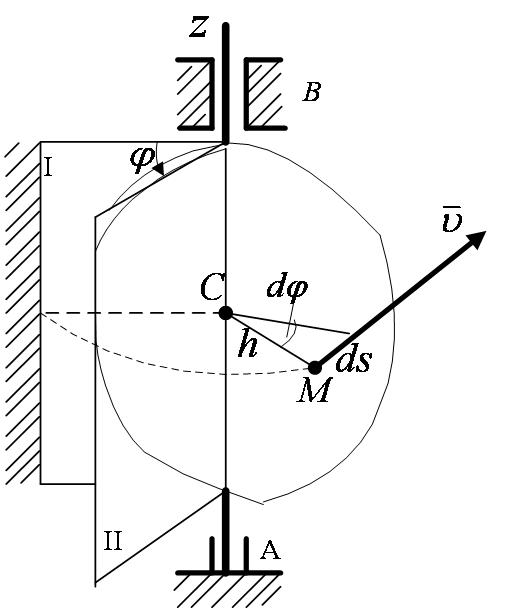

Проходящая через неподвижные точки A и В прямая АВ – ось вращения. Так как расстояния между точками твердого тела должны оставаться неизменными, то очевидно, что при вращательном движении все точки; принадлежащие оси вращения, будут неподвижны, а все остальные точки тела будут описывать окружности, плоскости которых перпендикулярны оси вращения, а центры лежат на этой оси.
Для определения положения вращающегося тела проведем через ось вращения, вдоль которой направим ось Az, полуплоскость I – неподвижную и полуплоскость II, врезанную в само тело и вращающуюся вместе с ним (рисунок 2_13).
Тогда положение тела в любой момент времени однозначно определится взятым с соответствующим знаком углом 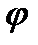 между этими полуплоскостями, который назовем углом поворота тела. Будем считать угол
между этими полуплоскостями, который назовем углом поворота тела. Будем считать угол 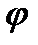 положительным, если он отложен от неподвижной плоскости в направлении против хода часовой стрелки, и отрицательным, если по ходу часовой стрелки.
положительным, если он отложен от неподвижной плоскости в направлении против хода часовой стрелки, и отрицательным, если по ходу часовой стрелки.
Чтобы знать положение тела в любой момент времени, надо знать зависимость угла 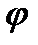 от времени
от времени 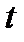 , т. е.
, т. е.
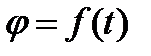
| (2.25) |
Уравнение (2.25) выражает закон вращательного движения твердого тела вокруг неподвижной оси.
Основными кинематическими характеристиками вращательного движения твердого тела являются его угловая скорость 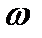 и угловое ускорение
и угловое ускорение  .
.
Если за промежуток времени  тело совершает поворот на угол
тело совершает поворот на угол 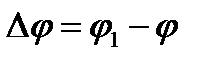 , то численно средней угловой скоростью тела за этот промежуток времени будет
, то численно средней угловой скоростью тела за этот промежуток времени будет 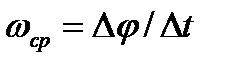 . В пределе при
. В пределе при 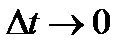 найдем, что
найдем, что
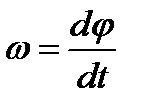 или или 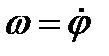 . .
| (2.26) |
Таким образом, числовое значение угловой скорости тела в данный момент времени равно первой производной от угла поворота, по времени. Знак 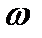 определяет направление вращения тела. Легко видеть, что когда вращение происходит против хода часовой стрелки,
определяет направление вращения тела. Легко видеть, что когда вращение происходит против хода часовой стрелки, 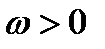 , а когда по ходу часовой стрелки, то
, а когда по ходу часовой стрелки, то 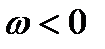 .
.
Угловую скорость тела можно изобразить в виде вектора 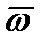 , модуль которого равен
, модуль которого равен 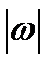 и который направлен вдоль оси вращения тела в ту сторону, откуда вращение видно происходящим против хода часовой стрелки (рисунки 2_14, 2_15).
и который направлен вдоль оси вращения тела в ту сторону, откуда вращение видно происходящим против хода часовой стрелки (рисунки 2_14, 2_15).
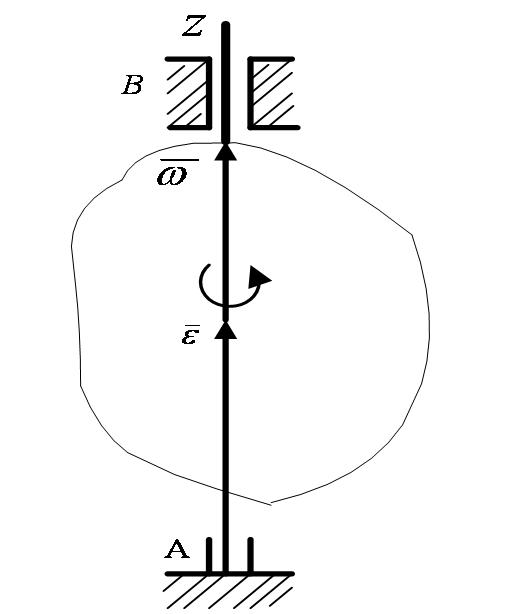
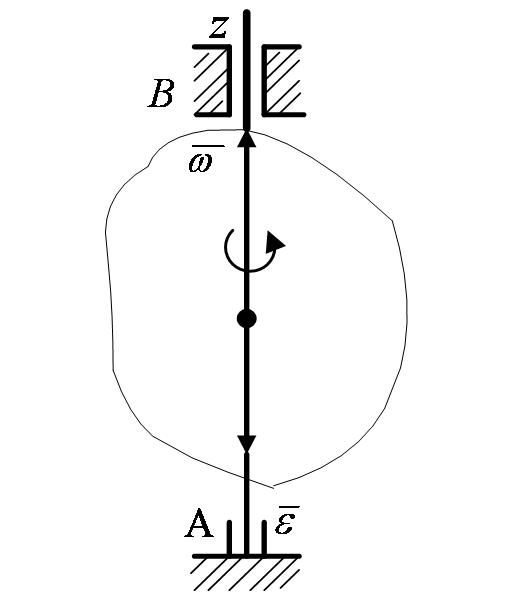
Такой вектор определяет сразу и модуль угловой скорости и ось вращения, и направление вращения вокруг этой оси.
Угловое ускорение характеризует изменение с течением времени угловой скорости тела. Если за промежуток времени  угловая скорость тела изменяется на величину
угловая скорость тела изменяется на величину 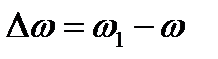 , то числовое значение среднего углового ускорения тела за этот промежуток времени будет
, то числовое значение среднего углового ускорения тела за этот промежуток времени будет 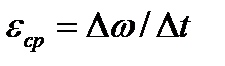 . В пределе при
. В пределе при 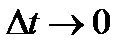 найдем, учтя одновременно равенство (2.26), что
найдем, учтя одновременно равенство (2.26), что
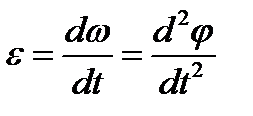 или или 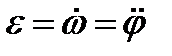 . .
| (2.27) |
Таким образом, числовое значение углового ускорения тела в данный момент времени равно первой производной от угловой скорости или второй производной от угла поворота тела по времени.
Если модуль угловой скорости со временем возрастает, вращение тела будет ускоренным, а если убывает – замедленным. Легко видеть, что вращение будет ускоренным, когда величины 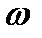 и
и 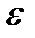 имеют одинаковые знаки, и замедленным – когда разные.
имеют одинаковые знаки, и замедленным – когда разные.
Угловое ускорение тела (по аналогии с угловой скоростью) можно также изобразить в виде вектора  , направленного вдоль оси вращения. При этом
, направленного вдоль оси вращения. При этом 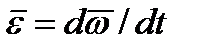 .
.
Направление 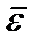 совпадает с направлением
совпадает с направлением 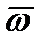 , когда тело вращается ускоренно (рисунок 2_14 – верхний, последний), и противоположно
, когда тело вращается ускоренно (рисунок 2_14 – верхний, последний), и противоположно  при замедленном вращении (рисунок 2_15 – нижний, последний).
при замедленном вращении (рисунок 2_15 – нижний, последний).
Равномерное и равнопеременное вращения
Термин равномерное движение.
Найдем закон равномерного вращения.
Из формулы (2.26) имеем 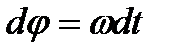 . Отсюда, считая, что в начальный момент времени
. Отсюда, считая, что в начальный момент времени 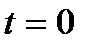 угол
угол 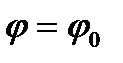 , и беря интегралы слева от
, и беря интегралы слева от 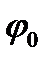 до
до 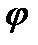 , а справа от 0 до
, а справа от 0 до 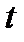 , получим окончательно
, получим окончательно

| (2.28) |
Из равенства (2.28) следует, что при равномерном вращении, когда 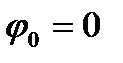 ,
,
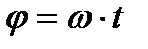 и и 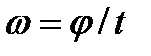 . .
| (2.29) |
В технике скорость равномерного, вращения часто определяют числом оборотов в минуту, обозначая эту величину через 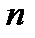 об/мин. Найдем зависимость между
об/мин. Найдем зависимость между 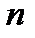 , об/мин и
, об/мин и 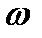 , 1/с. При одном обороте тело повернется на угол
, 1/с. При одном обороте тело повернется на угол 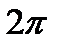 , а при
, а при 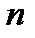 оборотах на
оборотах на 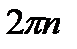 ; этот поворот делается за время t=1 мин = 60 с. Из равенства (2.29) следует тогда, что
; этот поворот делается за время t=1 мин = 60 с. Из равенства (2.29) следует тогда, что
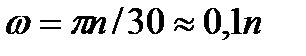
| (2.30) |
Термин равнопеременное движение.
Найдем закон равнопеременного вращения, считая, что в начальный момент времени 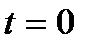 угол
угол 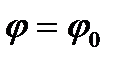 , а угловая скорость
, а угловая скорость 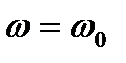 (
( 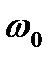 – начальная угловая скорость).
– начальная угловая скорость).
Из формулы (2.27) имеем 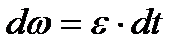 . Интегрируя левую часть в пределах от
. Интегрируя левую часть в пределах от 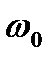 до
до 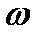 , а правую – в пределах от 0 до
, а правую – в пределах от 0 до 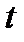 , найдем
, найдем
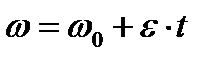
| (2.31) |
Представим выражение (2.31) в виде 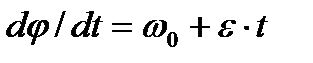 или
или 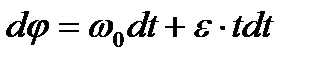 .
.
Вторично интегрируя, найдем отсюда закон равнопеременного вращения
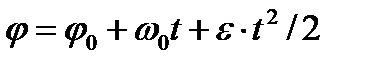
| (2.32) |
Угловая скорость  этого вращения определяется формулой (2.31). Если величины
этого вращения определяется формулой (2.31). Если величины 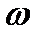 и
и 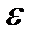 имеют одинаковые знаки, вращение будет равноускоренным, а если разные - равнозамедленным.
имеют одинаковые знаки, вращение будет равноускоренным, а если разные - равнозамедленным.
Скорости и ускорения точек вращающегося тела
Рассмотрим какую-нибудь точку M твердого тела, находящуюся на расстоянии 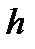 от оси вращения (рисунок 2_13).
от оси вращения (рисунок 2_13).

При вращении тела точка М будет описывать окружности радиуса А, плоскость которой перпендикулярна оси вращения, а центр С лежит на самой оси. Если за время 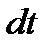 происходит элементарный поворот тела на угол
происходит элементарный поворот тела на угол 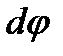 , то точка М при этом совершает вдоль своей траектории элементарное перемещение
, то точка М при этом совершает вдоль своей траектории элементарное перемещение 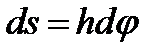 . Тогда числовое значение скорости точки будет равно отношению
. Тогда числовое значение скорости точки будет равно отношению 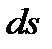 к
к 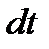 , т.е,
, т.е, 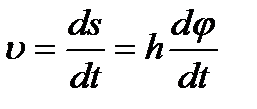 или
или
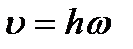
| (2.33) |
Скорость 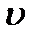 в отличие от угловой скорости тела называют иногда еще линейной или окружной скоростью точки М.
в отличие от угловой скорости тела называют иногда еще линейной или окружной скоростью точки М.
Таким образом, числовое значение скорости точки вращающегося твердого тела равно произведению угловой скорости тела на расстояние от той точки до оси вращения.
Направлена скорость по касательной к описываемой точкой окружности или перпендикулярно плоскости, проходящей через ось вращения и точку М.
Так как для всех точек тела 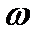 имеет в данный момент времени одно и то же значение, то из формулы (2.33) следует, что скорости точек вращающегося тела пропорциональны их расстояниям от оси вращения. Поле скоростей точек вращающегося твердого тела имеет вид, показанный на рисунке 2.16.
имеет в данный момент времени одно и то же значение, то из формулы (2.33) следует, что скорости точек вращающегося тела пропорциональны их расстояниям от оси вращения. Поле скоростей точек вращающегося твердого тела имеет вид, показанный на рисунке 2.16.

Для нахождения ускорения точки М воспользуемся формулами 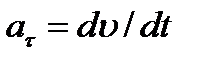 ,
, 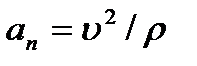 .
.
В нашем случае 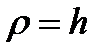 . Подставляя значение
. Подставляя значение 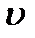 из равенства (2.33) в выражения
из равенства (2.33) в выражения  и
и 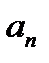 , получим
, получим 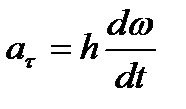 ,
, 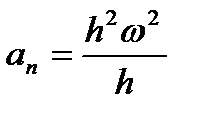 или окончательно:
или окончательно:
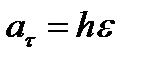 , , 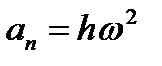 . .
| (2.34) |
Касательная составляющая ускорения 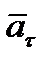 направлена по касательной к траектории (в сторону движения при ускоренном вращении тела и в обратную сторону при замедленном); нормальная составляющая
направлена по касательной к траектории (в сторону движения при ускоренном вращении тела и в обратную сторону при замедленном); нормальная составляющая 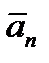 всегда направлена по радиусу МС к оси вращений (рисунок 2_17).
всегда направлена по радиусу МС к оси вращений (рисунок 2_17).
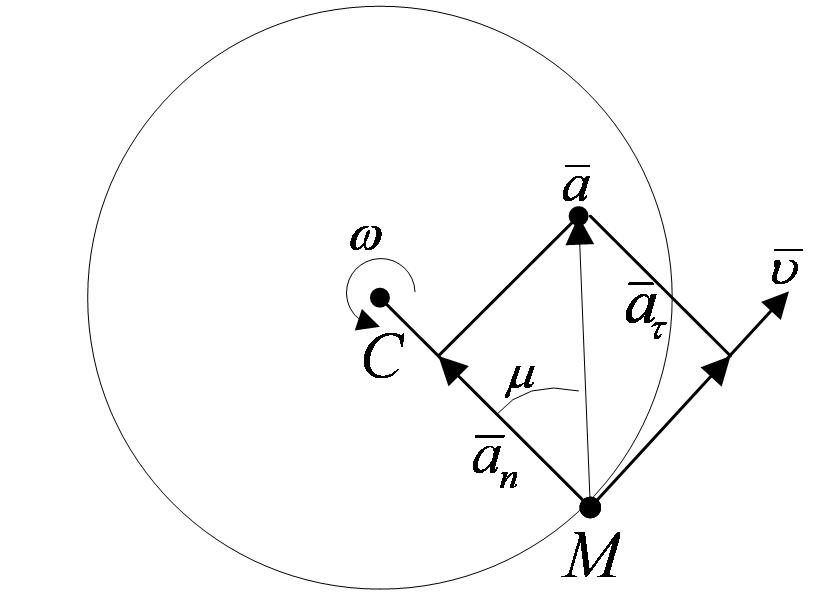
Полное ускорение точки М будет 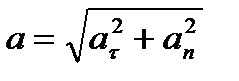 или
или
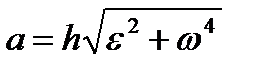
| (2.35) |
Отклонение вектора полного ускорения от радиуса описываемой точкой окружности определяется углом 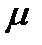 , который вычисляется по формуле
, который вычисляется по формуле 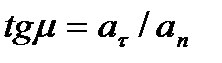 . Подставляя сюда значения
. Подставляя сюда значения 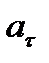 и
и 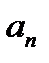 из равенств (2.34), получаем
из равенств (2.34), получаем
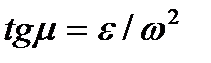 . .
| (2.36) |
Так как 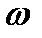 и
и 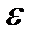 имеют в данный момент времени для всех точек тела одно и то же значение, то из формул (2.35) и (2.36) следует, что ускорения всех точек вращающегося твердого тела пропорциональны их расстояниям от оси вращения и образуют в данный момент времени один и тот же угол
имеют в данный момент времени для всех точек тела одно и то же значение, то из формул (2.35) и (2.36) следует, что ускорения всех точек вращающегося твердого тела пропорциональны их расстояниям от оси вращения и образуют в данный момент времени один и тот же угол 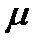 с радиусами описываемых ими окружностей. Поле ускорений точек вращающегося твердого тела имеет вид, показанный на рисунке 2_18.
с радиусами описываемых ими окружностей. Поле ускорений точек вращающегося твердого тела имеет вид, показанный на рисунке 2_18.
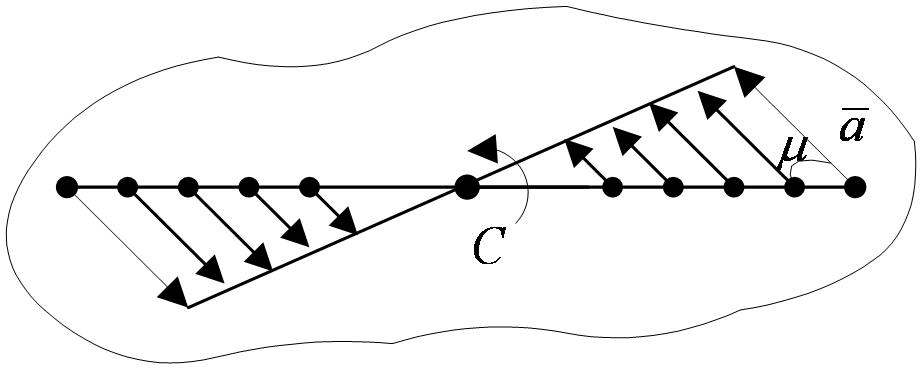
Формулы (2.33 – 2.36) позволяют определить скорость и ускорение любой точки тела; если известен закон вращения тела и расстояние данной точки от оси вращения. По этим же формулам можно, зная движение одной точки тела, найти движение любой другой его точки.
Дата добавления: 2021-06-28; просмотров: 682;











