Уравнения теплопроводности

Существуют три основные группы методов решения дифференциального уравнения теплопроводности: аналитические, численные и методы математического моделирования.

К аналитическим относятся классический метод непосредственного интегрирования, метод интегральных преобразований и метод источников. При методе непосредственного интегрирования дифференциального уравнения решение выполняют одним из известных способов. Покажем применение этого метода при решении одномерной стационарной задачи. Примером, иллюстрирующим такую задачу, является определение температурного поля в инструменте при иглофрезеровании.

В современном машиностроении используют процесс обработки деталей инструментом, поверхность которого (например, торец) снабжена большим количеством жестких металлических проволочек (игл). Такой инструмент позволяет повышать чистоту поверхности заготовки, придавать ей некоторое упрочнение. При назначении режима работы, в частности частоты вращения металлической щетки, важно рассчитать температуру иголки па рабочем торце, так как от нее зависит изнашивание инструмента и качество обработанной поверхности.

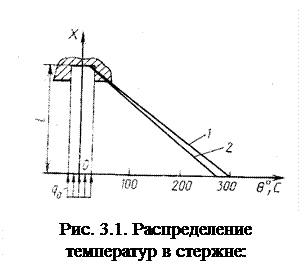
Схематизируя процесс, представим иголку как стержень, на торце которого действует источник теплоты, возникающий в результате преобразования механической энергии трения в тепловую (рис. 3.1).

Граничные условия:

а) на нижнем торце иголки задана плотность теплового потока, т, е. ГУ2:

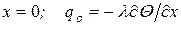; (3.6)

б) поскольку конец проволочки заделан в массивный корпус инструмента и не успевает прогреваться, можно предположить, что на верхнем торце температура равна температуре окружающей среды т. е. имеем типичный случай пассивной границы с ГУ1:

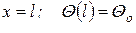; (3.7)

в) теплоотдачей с боковой поверхности проволочки, т.е. считать эту поверхность адиабатической; кроме того, при обработке достаточно широких поверхностей быстро устанавливается:

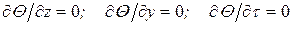. (3.8)

Тогда дифференциальное уравнение теплопроводности приводится к виду:

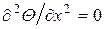. (3.9)

Интегрируя это уравнение первый раз, получаем 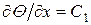. Далее, разделив переменные 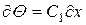и интегрируя второй раз, имеем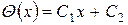

Для определения постоянных интегрирования используем граничные условия (3.6) и (3.7). Тогда:

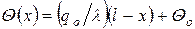. (3.10)

Выражение (3.10) представляет собой решение дифференциального уравнения теплопроводности для одномерной задачи. Оно показывает, что при принятых условиях однозначности изменение температуры по длине стержня подчинено линейному закону.

Обратим внимание на то, что, решая задачу о распространении теплоты в стержне, мы не учитывали зависимость коэффициента теплопроводности- от температуры. Если бы было необходимо учесть зависимость λ(Θ), то при линейной зависимости λ(Θ)= λ_о+m Θ_о , интегрирование приводит к выражению:

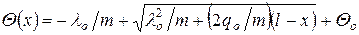. (3.11)

На рис. 3.1 сопоставлены законы изменения -температур по длине иголки, изготовленной из стали, для которой λ = 42—0,02Θ при (q_o = 400 Вт/м, l== 0,03м, Θ_о = 20°С. Как видно, распределение температур здесь мало отличается от линейного закона, причем наибольшее различие между температурами, рассчитанными по формулам (3.10) и (3.11), не выходит за пределы 6 %.

Лекция 4. Метод источников теплоты

1. Основные положения метода источников теплоты

2. Мгновенные точечные источники в неограниченных телах и

интегральные переходы