Движущиеся источники

Температурное поле для полосового движущегося источника:

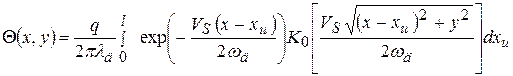, (2.8)

где x, y – абсцисса и ордината точки, для которой рассчитывается температура; x_u – абсцисса импульса теплоты; V_S – скорость перемещения источника.

К₀(u) – модифицированная функция Бесселя, которая с погрешностью, не выходящей за 5% может быть определена следующим образом:

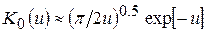. (2.9)

Переходим к безразмерным величинам y = x/l; y_и = x_и/l; n = y/l:

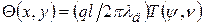. (2.10)

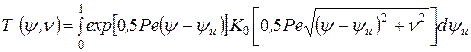, (2.11)

где Pe = Vl/ω_д - безразмерный критерий Пекле; Т(y,n) - безразмерное распределение температур.

Температурное поле в детали для полосового быстродвижущегося источника:

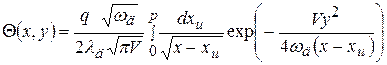, (2.12)

где x_u – абсцисса импульса теплоты; x, y – абсцисса и ордината точки, для которой рассчитывается температура; p= l, если x³ l, p= x, если x< l.

Переходим к безразмерным величинам y = x/l; y_и = x_и/l; n = y/l:

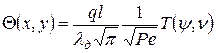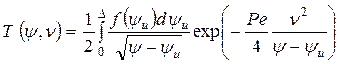; , (2.13)

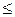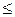где Pe = Vl/ω_д - критерий Пекле; D - верхний предел интеграла: D = y при 0 y 1 и D = 1 при y > 1;f(y_и) - закон распределения плотности теплового потока.

Распределения безразмерных температур на поверхности детали Т(y) (координата n = 0) и по глубине детали Т(n) (координата y = 1):

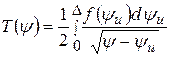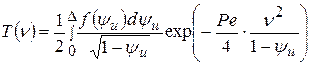; . (11)

Максимальная безразмерная температура на передней поверхности Т(0.5,0) имеет место в точке координатами ψ = 0,5; ζ = 0

; ;

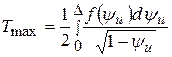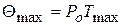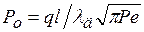
где Р_о – размерный коэфициент.
Лекция 6. Закономерности протекания тепловых процессов в деталях

при различных методах механообработки