И интегральные переходы

Температурное поле, возникающее под действием источника сложной формы, получают методом суперпозиции (наложения) полей, возникающих под действием каждого из мгновенных точечных источников. Математическое выражение, описывающее температурное поле, возникающее под действием мгновенного точечного источника, имеет вид:

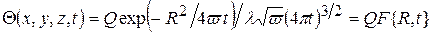, (4.5)

где Q - количество теплоты, внесенной в тело источником; t -время, прошедшее от момента теплового импульса; R- расстояние от места вспышки J(х_и у_и,z_и)до какой-либо точки тела М(х,у,z):

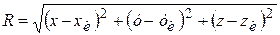(4.6)

Чтобы описать температурные поля, возникающие под действием различных источников теплоты, совершают интегральные переходы:

1) от точечного источника к одно-, двух- или трехмерному:

для одномерного источника, расположенного параллельно оси Z, представляемогов виде множества одновременно действующих элементарных точечных источников, полное повышение температуры тела под действием всех точечных источников, образующих одномерный, получим, совершая интегральный переход:

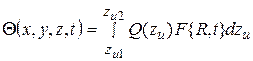. (4.7)

2) от мгновенного источника к действующему непрерывно:

непрерывное действие источника имитируем серией мгновенных тепловых импульсов, следующих друг за другом. Все мгновенные точечные источники, следовавшие друг за другом с интервалом времени dt вызовут в точке М (х у z) к моменту наблюдения τ повышение температуры

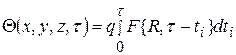, (4.8)

где q - количество теплоты, выделяемое источником в единицу времени.

3) от мгновенного источника к движущемуся:

для движущегося источника расстояние R является переменной величиной, поскольку координаты источника непрерывно меняются во времени. Например, если источник движется вдоль оси Х соскоростью V:

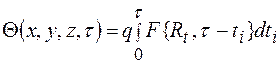, (4.9)

где .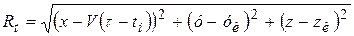

Лекция 5. Использование метода источников для решения различных задач

1. Мгновенные линейные и плоские источники

2. Непрерывно действующие источники

3. Движущиеся источники