Уравнения касательной и нормали
 Рассмотрим кривую, уравнение которой есть
Рассмотрим кривую, уравнение которой есть 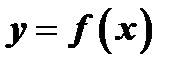 . Возьмем на этой кривой точку
. Возьмем на этой кривой точку 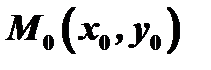 и напишем уравнение касательной к данной кривой в точке
и напишем уравнение касательной к данной кривой в точке 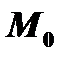 , предполагая, что эта касательная не параллельна оси ординат (рис. 4а). Уравнение прямой с угловым коэффициентом
, предполагая, что эта касательная не параллельна оси ординат (рис. 4а). Уравнение прямой с угловым коэффициентом 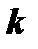 , проходящей через точку
, проходящей через точку 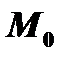 , имеет вид
, имеет вид
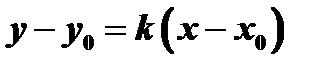 ,
,
но из геометрического смыла касательной имеем 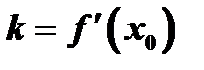 , поэтому уравнение касательной имеет вид
, поэтому уравнение касательной имеет вид
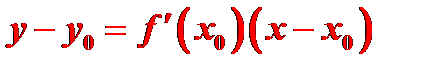
Наряду с касательной к кривой в данной точке очень часто приходится рассматривать нормаль.
Определение. Нормалью к кривой в данной точке называется прямая, проходящая через эту точку, перпендикулярную к касательной в этой точке.
Из определения нормали следует, что 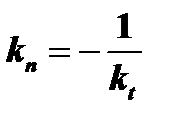 . Следовательно, уравнение нормали к кривой в точке
. Следовательно, уравнение нормали к кривой в точке 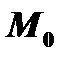 имеет вид
имеет вид
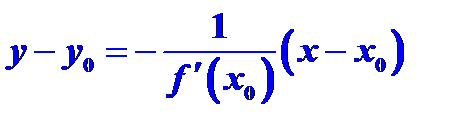
Длина 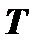 отрезка
отрезка 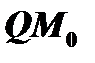 касательной, заключенного между точкой касания и осью абсцисс, называется длиной касательной. Проекция этого отрезка на ось абсцисс, т.е. отрезок
касательной, заключенного между точкой касания и осью абсцисс, называется длиной касательной. Проекция этого отрезка на ось абсцисс, т.е. отрезок 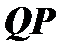 , называется подкасательной; длина подкасательной обозначается через
, называется подкасательной; длина подкасательной обозначается через 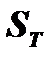 . Длина
. Длина 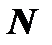 отрезка
отрезка 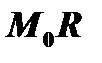 называется длиной нормали, а проекция
называется длиной нормали, а проекция 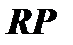 отрезка
отрезка 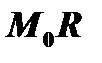 на ось абсцисс называется поднормалью; длина поднормали обозначается через
на ось абсцисс называется поднормалью; длина поднормали обозначается через 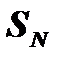 .
.
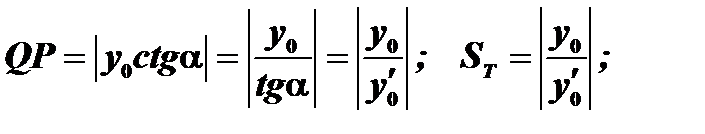
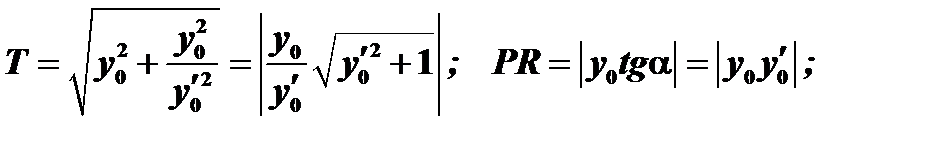
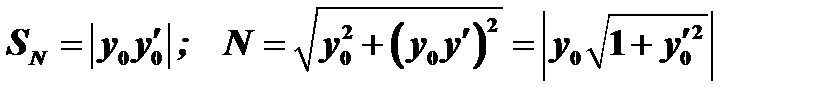
Дата добавления: 2016-06-05; просмотров: 2274;











