Исследование функции
С помощью производной можно изучить различные свойства функций. Ниже доказаны теоремы о тех или иных свойствах функций.
Условия монотонности функции. Пусть функция  определена в промежутке
определена в промежутке 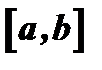 . Рассмотрим две точки
. Рассмотрим две точки 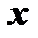 и
и 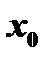 этого промежутка и соответствующие приращения аргумента
этого промежутка и соответствующие приращения аргумента 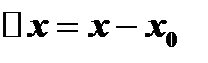 и функции
и функции 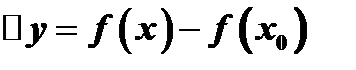 .
.
Теорема. Если в промежутке 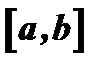 функция
функция  дифференцируема и возрастает (убывает), то ее производная в этом промежутке не отрицательна (не положительна), т.е.
дифференцируема и возрастает (убывает), то ее производная в этом промежутке не отрицательна (не положительна), т.е. 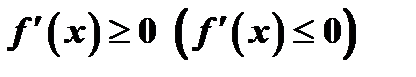 .
.
Действительно, если 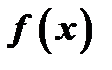 возрастающая, то
возрастающая, то 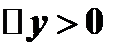 при
при 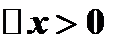 и
и 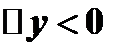 при
при 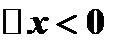 . В обоих случаях
. В обоих случаях  , а следовательно,
, а следовательно, 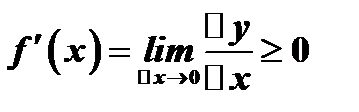 .
.
Теорема. Если функция  непрерывна в
непрерывна в 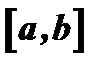 и дифференцируема в
и дифференцируема в 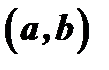 , причем
, причем 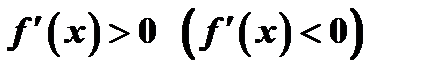 , то эта функция возрастает (убывает) в
, то эта функция возрастает (убывает) в 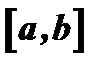 .
.
Действительно, согласно формуле конечных приращений для произвольных 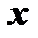 и
и 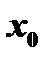 из
из 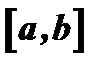 имеем
имеем 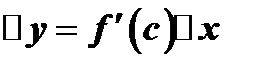 . Следовательно, если
. Следовательно, если 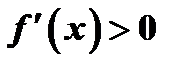 в
в 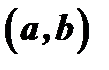 и
и 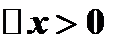 , то
, то 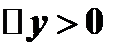 и данная функция возрастает в
и данная функция возрастает в 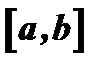 . Если же
. Если же 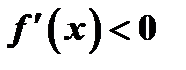 и
и 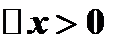 , то
, то 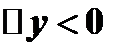 и функция убывает.
и функция убывает.
Максимум и минимум функции. Экстремумы. Пусть функция  непрерывна в промежутке
непрерывна в промежутке 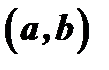 и
и 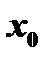 - точка этого промежутка.
- точка этого промежутка.
 Определение. Функция
Определение. Функция 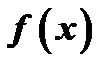 имеет в точке
имеет в точке 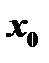 максимум (минимум), если значение функции
максимум (минимум), если значение функции 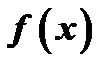 в точке
в точке 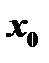 является наибольшим (наименьшим) среди ее значении в какой-либо окрестности точки
является наибольшим (наименьшим) среди ее значении в какой-либо окрестности точки 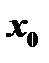 .
.
Это значит существует такое число 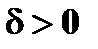 , что
, что 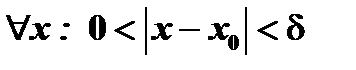 , выполняется неравенство
, выполняется неравенство 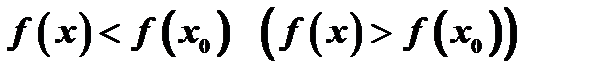 .
.
Если функция имеет в точке 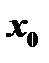 максимум или минимум, то говорят, что она имеет в этой точке экстремум, а сама точка
максимум или минимум, то говорят, что она имеет в этой точке экстремум, а сама точка 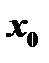 называется точкой экстремума. Из определения следует, что понятие экстремума носит локальный характер в том смысле, что в случае экстремума неравенства
называется точкой экстремума. Из определения следует, что понятие экстремума носит локальный характер в том смысле, что в случае экстремума неравенства 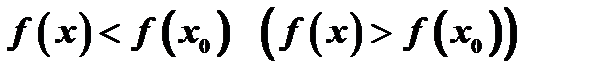 не обязаны выполняться для всех значений
не обязаны выполняться для всех значений 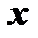 в области определения функции, а лишь в некоторой окрестности точки
в области определения функции, а лишь в некоторой окрестности точки 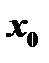 (за исключением
(за исключением 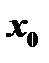 ).
).
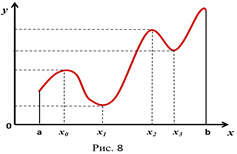
В случае максимума график функции имеет вершину, и точке максимума 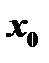 соответствует ордината
соответствует ордината 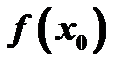 , наибольшая среди соседних ординат. Очевидно, функция может иметь несколько максимумов, причем иной максимум может быть меньше другого минимума. На рис.8
, наибольшая среди соседних ординат. Очевидно, функция может иметь несколько максимумов, причем иной максимум может быть меньше другого минимума. На рис.8 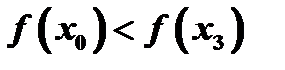 .
.
Наибольшее значение функции в промежутке 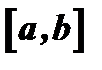 - это не обязательно наибольший из максимумов; это может быть значение функции на границе промежутка, например в точке
- это не обязательно наибольший из максимумов; это может быть значение функции на границе промежутка, например в точке  (рис.8).
(рис.8).
Н е о б х о д и м о е у с л о в и е с у щ е с т в о в а н и я э к с т р е м у м а.
Теорема. Если дифференцируемая в окрестности точки 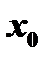 функция
функция 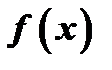 имеет в этой точке экстремум, то
имеет в этой точке экстремум, то  .
.
В сущности это другая формулировка теоремы Ферма, все условия здесь выполнены, а поэтому имеет место и ее заключение.
 Для дифференцируемой функции
Для дифференцируемой функции 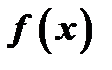 условие
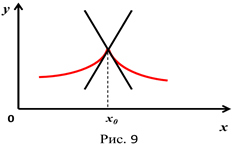
условие 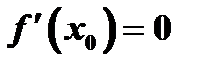 является необходимым условием экстремума. Функция может имеет в точке экстремум и не быть в этой точке дифференцируемой (рис.9). Следовательно необходимо, чтобы в точке экстремума производная функции либо не существовала, либо была равна нулю.
является необходимым условием экстремума. Функция может имеет в точке экстремум и не быть в этой точке дифференцируемой (рис.9). Следовательно необходимо, чтобы в точке экстремума производная функции либо не существовала, либо была равна нулю.
Значения аргумента, при которых производная равна нулю или имеет разрыв, называются критическими значениями.
Д о с т а т о ч н о е у с л о в и е с у щ е с т в о в а н и я э к с т р е м у м а. Условимся в следующем: будем говорить, что «производная меняет знак с плюса на минус при переходе через точку 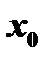 », если в некоторой окрестности точки
», если в некоторой окрестности точки 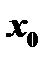 выполняются неравенства:
выполняются неравенства:  и
и  . Аналогично, если
. Аналогично, если  и
и  , то производная меняет знак с минуса на плюс при переходе через
, то производная меняет знак с минуса на плюс при переходе через 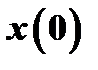 .
.
Теорема. Пусть функция 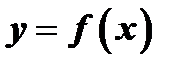 непрерывна и дифференцируема в некоторой окрестности критической точки
непрерывна и дифференцируема в некоторой окрестности критической точки  (в самой точке
(в самой точке  производная может не существовать). Если при переходе через точку
производная может не существовать). Если при переходе через точку  производная
производная 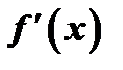 меняет знак с плюса на минус (с минуса на плюс), то в точке
меняет знак с плюса на минус (с минуса на плюс), то в точке  функция имеет максимум (минумум).
функция имеет максимум (минумум).
Доказательство. Предположим, что производная меняет знак с плюса на минус. Рассмотрим значение 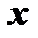 , меньшее
, меньшее  , и напишем формулу конечных приращений для
, и напишем формулу конечных приращений для 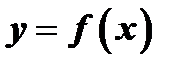 и промежутка
и промежутка 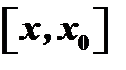 :
: 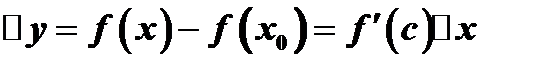 , где
, где 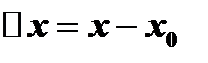 и
и 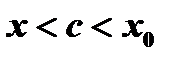 . По условию при
. По условию при 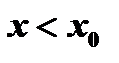
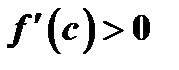 и поэтому
и поэтому 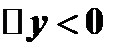 , т.е.
, т.е. 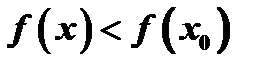 .
.
Если же 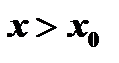 , то из аналогичной формулы Лагранжа и условия
, то из аналогичной формулы Лагранжа и условия 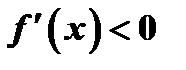 следует, что
следует, что 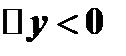 , т.е. опять
, т.е. опять 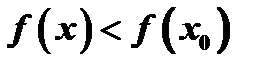 . Итак, в обоих случаях
. Итак, в обоих случаях 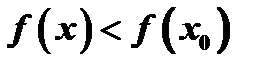 , и в соответствии с определением понятия максимума функция
, и в соответствии с определением понятия максимума функция 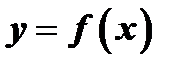 имеет максимум в точке
имеет максимум в точке  .
.
Аналогично доказывается вторая часть теоремы.
Отсюда следует п р а в и л о исследования функции на экстремум с помощью первой производной. Пусть в 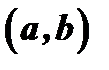 дана функция
дана функция 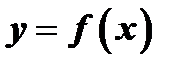 :
:
1) находим первую производную,
2) находим критические значения,
3) выясняем знак  слева и справа от каждой критической точки,
слева и справа от каждой критической точки,
4) выносим суждение об экстремуме в соответствии с теоремой о достаточном условии существования экстремума,
5) вычисляем значения функции в точках экстремума.
Достаточное условие существования экстремума можно выяснить и с помощью второй производной на основании теоремы, которую мы приводим без доказательства:
Теорема. Пусть функция 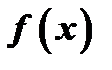 имеет в точке
имеет в точке 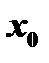 и ее окрестности непрерывные первую и вторую производные, причем
и ее окрестности непрерывные первую и вторую производные, причем 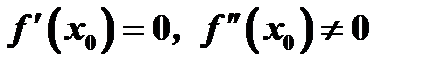 . Тогда функция
. Тогда функция 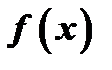 имеет в точке
имеет в точке 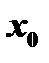 максимум (минимум), если
максимум (минимум), если  .
.
Для нахождения наибольшего и наименьшего значений функции в промежутке 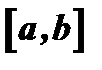 можно поступить так: 1) найти критические значения
можно поступить так: 1) найти критические значения 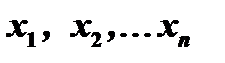 и присоединить к ним точки
и присоединить к ним точки 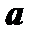 и
и  , 2) вычислить значения функции в каждой из этих точек и выбрать среди этих значений наибольшее и наименьшее.
, 2) вычислить значения функции в каждой из этих точек и выбрать среди этих значений наибольшее и наименьшее.
 Выпуклость и вогнутость. Точки перегиба. Пусть функция
Выпуклость и вогнутость. Точки перегиба. Пусть функция 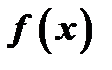 дифференцируема в промежутке
дифференцируема в промежутке 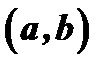 . Тогда ее график имеет касательную в каждой точке. Кривая называется выпуклой (вогнутой) в промежутке
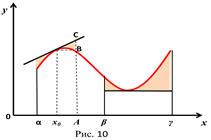
. Тогда ее график имеет касательную в каждой точке. Кривая называется выпуклой (вогнутой) в промежутке 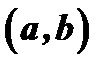 , если все ее точки лежат ниже (выше) любой ее касательной в этом промежутке (рис.10). Из этого определения следует, что на участке выпуклости, так же как и на участке вогнутости, касательные к графику функции не пересекаются с самим графиком и имеют с ним каждая свою единственную общую точку – точку касания. Точки, отделяющие выпуклые части графика функции от его вогнутых частей, называются точками перегиба. Очевидно, что в точке перегиба касательная пересекает график, т.к. с одной стороны от этой точки кривая лежит под касательной, а с другой над нею.
, если все ее точки лежат ниже (выше) любой ее касательной в этом промежутке (рис.10). Из этого определения следует, что на участке выпуклости, так же как и на участке вогнутости, касательные к графику функции не пересекаются с самим графиком и имеют с ним каждая свою единственную общую точку – точку касания. Точки, отделяющие выпуклые части графика функции от его вогнутых частей, называются точками перегиба. Очевидно, что в точке перегиба касательная пересекает график, т.к. с одной стороны от этой точки кривая лежит под касательной, а с другой над нею.
Для решения вопроса о направлении вогнутости кривой, заданной уравнением 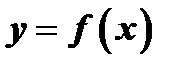 , рассмотрим в окрестности точки
, рассмотрим в окрестности точки 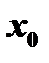 знак разности
знак разности 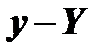 между ординатой графика функции графика функции
между ординатой графика функции графика функции 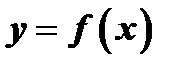 и ординатой
и ординатой 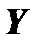 точки
точки 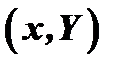 касательной к этому графику в точке
касательной к этому графику в точке 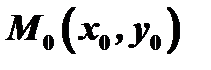 :
: 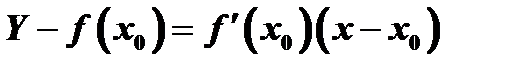 . Поэтому разность ординат, преобразованная с помощью формулы конечных приращений, будет равна
. Поэтому разность ординат, преобразованная с помощью формулы конечных приращений, будет равна
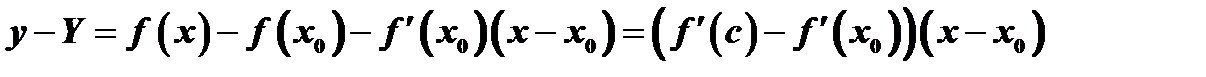 .
.
Используя еще раз формулу конечных приращений применительно к функции 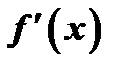 , получим
, получим
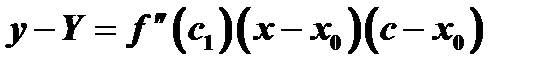 ,
,
где произведение  всегда положительно. Следовательно, знак левой части вполне определяется знаком второй производной: если
всегда положительно. Следовательно, знак левой части вполне определяется знаком второй производной: если  , то
, то 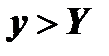 и кривая вогнута, если
и кривая вогнута, если  , то
, то 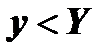 и кривая выпукла. Таким образом пришли к следующему утверждению:
и кривая выпукла. Таким образом пришли к следующему утверждению:
Теорема. Пусть в промежутке 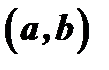 функция
функция  имеет вторую производную, которая сохраняет знак. Тогда кривая
имеет вторую производную, которая сохраняет знак. Тогда кривая 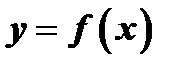 в этом промежутке выпукла (вогнута), если в
в этом промежутке выпукла (вогнута), если в 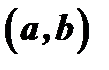 выполнено условие
выполнено условие 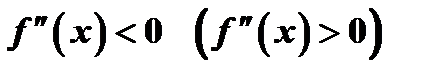 .
.
В точке перегиба вторая производная может не существовать.
Асимптоты. Перейдем к изучению бесконечных ветвей графика функции 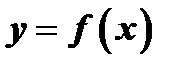 , если такие ветви имеются. Бесконечной ветвью кривой называется такая ее часть, на которой имеются точки, сколь угодно далекие от начала координат. Например, окружность не имеет бесконечной ветви, а парабола имеет две бесконечных ветви.
, если такие ветви имеются. Бесконечной ветвью кривой называется такая ее часть, на которой имеются точки, сколь угодно далекие от начала координат. Например, окружность не имеет бесконечной ветви, а парабола имеет две бесконечных ветви.
 Асимптотой бесконечной ветви кривой называется прямая расстояние
Асимптотой бесконечной ветви кривой называется прямая расстояние 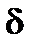 до которой от точки
до которой от точки 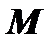 кривой стремится к нулю когда точка
кривой стремится к нулю когда точка 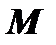 вдоль этой ветви неограниченно удаляется от начала координат. Если обозначить через
вдоль этой ветви неограниченно удаляется от начала координат. Если обозначить через 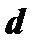 расстояние от начала координат до точки
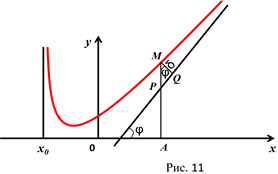
расстояние от начала координат до точки 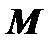 (рис.11), то
(рис.11), то  . Различают асимптоты вертикальные и наклонные.
. Различают асимптоты вертикальные и наклонные.
В е р т и к а л ь н ы е а с и м п т о т ы. Из определения асимптоты следует, что если 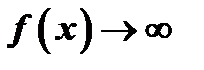 при
при 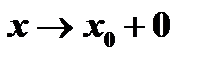 , или при
, или при 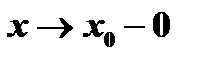 , или при
, или при 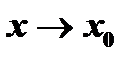 , то прямая
, то прямая 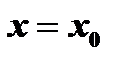 есть асимптота кривой
есть асимптота кривой 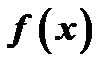 (рис.11).
(рис.11).
Правило нахождения вертикальных асимптот таково: 1) находим точки разрыва функции, 2) исследуем поведение функции при стремлении аргумента слева и справа к каждой из этих точек. Если при этом окажется, что 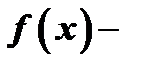 функция бесконечно большая, то
функция бесконечно большая, то 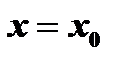 есть уравнение вертикальной асимптоты.
есть уравнение вертикальной асимптоты.
Н а к л о н н ы е а с и м п т о т ы изображаются уравнением вида 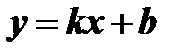 . Заметим, что если бесконечная ветвь имеет наклонную асимптоту (с углом наклона
. Заметим, что если бесконечная ветвь имеет наклонную асимптоту (с углом наклона 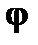 ), то вместе с условием
), то вместе с условием  будет выполнено условие
будет выполнено условие  , т.к.
, т.к. 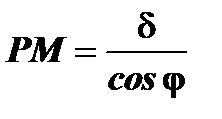 , где
, где  (рис.11). Здесь величина
(рис.11). Здесь величина 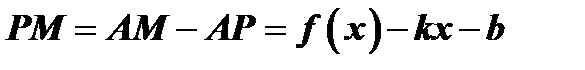 , поэтому имеем
, поэтому имеем 
 ,
,
т.е. разность ординат кривой и асимптоты есть величина бесконечно малая при 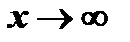 . Но тогда и величина
. Но тогда и величина 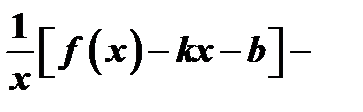 бесконечно малая. Поэтому
бесконечно малая. Поэтому
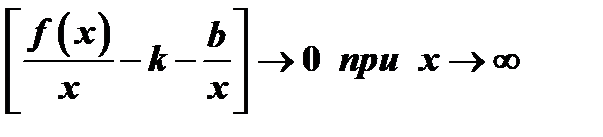 .
.
Отсюда следует, что
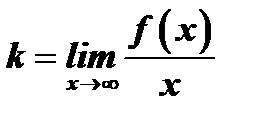 .
.
Зная 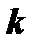 , находим величину
, находим величину 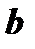 из равенства
из равенства 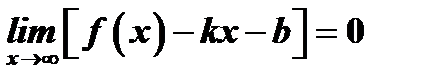 :
:
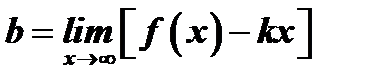
Общая схема исследования функции. Пусть дана функция 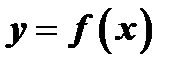 . Можно рекомендовать следующую схему ее исследования:
. Можно рекомендовать следующую схему ее исследования:
1) находим область определения функции;
2) находим точки разрыва функции и односторонние пределы в этих точках;
3) находим точки пересечения с осями координат;
4) выясняем периодичность функции;
5) выясняем четность или нечетность функции;
6) находим промежутки возрастания и убывания функции, экстремумы;
7) находим промежутки выпуклости и вогнутости функции, точки перегиба;
8) находим асимптоты кривой;
9) при недостаточности сведений о кривой находим дополнительные точки;
10) строим график функции.
Дата добавления: 2016-06-05; просмотров: 2036;











