Задачи, приводящие к понятию производной.
З а д а ч а о с к о р о с т и д в и ж у щ е й с я т о ч к и . Рассмотрим движущуюся прямолинейно точку. Пройденный ею путь 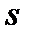 , отсчитываемый от определенной точки прямой, есть функция времени
, отсчитываемый от определенной точки прямой, есть функция времени 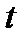 . Движение считается заданным, когда известно уравнение движения:
. Движение считается заданным, когда известно уравнение движения: 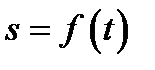 . Требуется найти скорость движущейся точки.
. Требуется найти скорость движущейся точки.
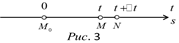 Рассмотрим два момента времени
Рассмотрим два момента времени 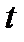 и
и 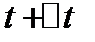 . Моменту времени
. Моменту времени 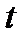 соответствует положение точки
соответствует положение точки 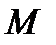 и пройденный ею путь, равный
и пройденный ею путь, равный 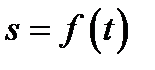 . Моменту времени
. Моменту времени 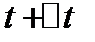 соответствует положение точки
соответствует положение точки 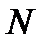 и пройденный ею путь
и пройденный ею путь 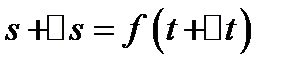 (рис. 3). Поэтому за промежуток времени между
(рис. 3). Поэтому за промежуток времени между 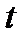 и
и 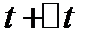 точка пройдет путь, равный
точка пройдет путь, равный 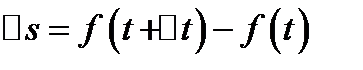 . Средняя скорость на участке пути
. Средняя скорость на участке пути 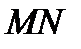 равна
равна 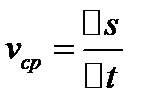 . Эта скорость воображаемого равномерного движения. Средняя скорость меняется вместе с изменением
. Эта скорость воображаемого равномерного движения. Средняя скорость меняется вместе с изменением 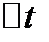 и тем лучше характеризует движение в промежутке
и тем лучше характеризует движение в промежутке 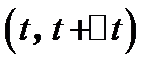 , чем меньше
, чем меньше 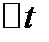 . Поэтому правильное представление о скорости движения дает предел средней скорости при стремлении
. Поэтому правильное представление о скорости движения дает предел средней скорости при стремлении 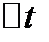 к нулю. Скоростью точки в данный момент времени
к нулю. Скоростью точки в данный момент времени 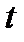 зазывают предел средней скорости при стремлении
зазывают предел средней скорости при стремлении 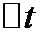 к нулю:
к нулю:
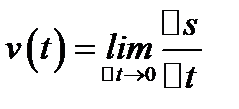 .
.
 З а д а ч а о к а с а т е л ь н о й к д а н н о й к р и в о й . Касательной к кривой в данной ее точке
З а д а ч а о к а с а т е л ь н о й к д а н н о й к р и в о й . Касательной к кривой в данной ее точке 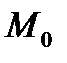 называется предельное положение секущей
называется предельное положение секущей 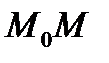 , когда точка
, когда точка 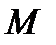 вдоль по кривой стремится к точке
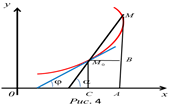
вдоль по кривой стремится к точке 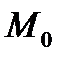 (рис. 4). Угловым коэффициентом прямой ( в частности, касательной) называется тангенс угла, образованного этой прямой с осью
(рис. 4). Угловым коэффициентом прямой ( в частности, касательной) называется тангенс угла, образованного этой прямой с осью 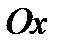 (угол отсчитывается от оси
(угол отсчитывается от оси 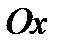 против часовой стрелки); он обозначается обычно буквой
против часовой стрелки); он обозначается обычно буквой 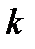 . Требуется найти угловой коэффициент касательной к кривой, заданной уравнением
. Требуется найти угловой коэффициент касательной к кривой, заданной уравнением 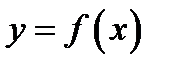 в точке
в точке 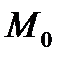 с абсциссой
с абсциссой 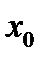 . Для этого возьмем на кривой точку
. Для этого возьмем на кривой точку 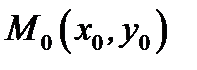 и близкую к ней точку
и близкую к ней точку 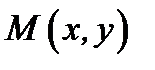 . Проведем секущую
. Проведем секущую 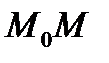 и обозначим через
и обозначим через 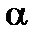 угол наклона секущей. Согласно построению (рис. 4) имеем
угол наклона секущей. Согласно построению (рис. 4) имеем 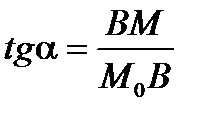 , где
, где 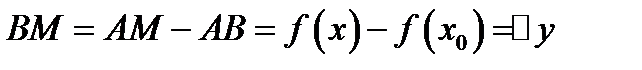 ,
, 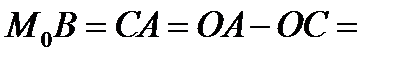
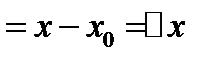 . Следовательно,
. Следовательно, 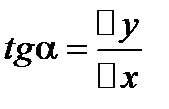 . Если теперь устремить
. Если теперь устремить 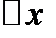 к нулю, то точка
к нулю, то точка 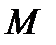 , перемещаясь вдоль по кривой, устремится к точке
, перемещаясь вдоль по кривой, устремится к точке 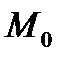 , а угол
, а угол 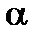 будет стремиться к
будет стремиться к 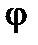 (если кривая имеет касательную в точке
(если кривая имеет касательную в точке 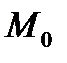 ). Зная угловой коэффициент секущей, исходя из определения касательной как предельного положения секущей, можем найти угловой коэффициент касательной
). Зная угловой коэффициент секущей, исходя из определения касательной как предельного положения секущей, можем найти угловой коэффициент касательной 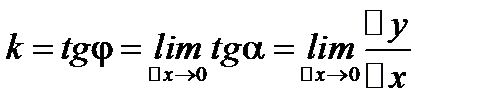 .
.
Если сопоставить операции, которые были выполнены при решении задач, и отвлечься от различия в истолковании переменных, то мы увидим, что каждый раз приращение функции делилось на приращение независимой переменной и затем вычислялся предел их отношения. Так приходим к основному понятию дифференциального исчисления – к понятию производной.
Пусть функция 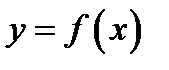 определена в некоторой окрестности фиксированного
определена в некоторой окрестности фиксированного 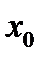 . Рассмотрим точку
. Рассмотрим точку 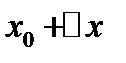 из этой окрестности и вычислим соответствующее приращение функции
из этой окрестности и вычислим соответствующее приращение функции 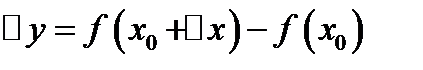 .
.
Определение. Производной функции 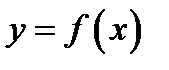 по независимой переменной
по независимой переменной 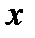 при данном значении
при данном значении 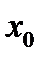 называется конечный предел отношения приращения функции
называется конечный предел отношения приращения функции 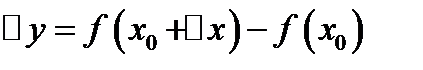 к вызвавшему его приращению независимой переменной
к вызвавшему его приращению независимой переменной 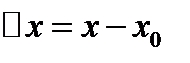 при стремлении
при стремлении 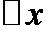 к нулю, если этот предел существует:
к нулю, если этот предел существует:
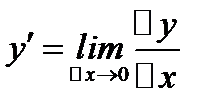 .
.
Для обозначения производной приняты следующие символы: 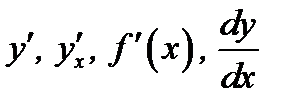 .
.
Если отношение 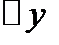 к
к 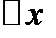 при
при 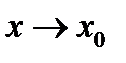 имеет предел справа (или слева), то он называется производной справа (или слева). Такие пределы называются односторонними производными.
имеет предел справа (или слева), то он называется производной справа (или слева). Такие пределы называются односторонними производными.
Операция нахождения производной функции называется ее дифференцированием.
Геометрическое значение производной установлено при решении задачи о касательной к данной кривой: производная функции 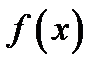 в точке
в точке 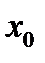 численно равна угловому коэффициенту касательной к графику функции
численно равна угловому коэффициенту касательной к графику функции 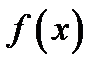 в точке
в точке 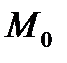 с абсциссой
с абсциссой 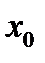 .
.
Механическое значение производной установлено при решении задачи о скорости движущейся точки: скорость прямолинейно движущейся точки есть производная от пройденного пути по времени.
Из определения производной вытекает схема ее вычисления:
1. Пусть дана функция 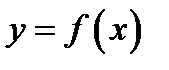 . Даем независимой переменной
. Даем независимой переменной 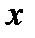 приращение
приращение 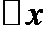
2. Находим соответствующее приращение функции 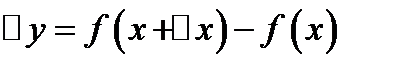
3. Составляем отношение 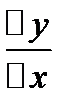
4. Находим предел этого отношения и получаем производную 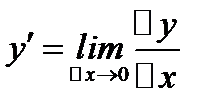 .
.
Дата добавления: 2016-06-05; просмотров: 2820;











