Непрерывность функции
Пусть функция 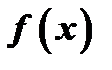 определена в точке
определена в точке 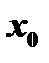 и некоторой ее окрестности.
и некоторой ее окрестности.
Определение. Функция 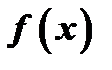 называется непрерывной в точке
называется непрерывной в точке 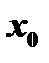 , если существует предел
, если существует предел 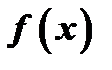 при стремлении
при стремлении 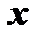 к
к 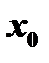 и этот предел равен значению функции в точке
и этот предел равен значению функции в точке 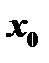 :
:
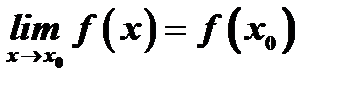
Если это условие не выполнено, то точка 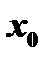 называется точкой разрыва функции
называется точкой разрыва функции 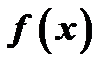 .
.
Для непрерывности функции 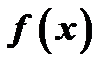 в точке
в точке 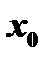 необходимо (как, впрочем, и достаточно), чтобы она была определена в этой точке, чтобы существовали односторонние пределы слева и справа:
необходимо (как, впрочем, и достаточно), чтобы она была определена в этой точке, чтобы существовали односторонние пределы слева и справа: 
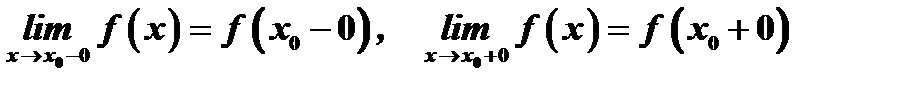 и чтобы имело место равенство трех чисел
и чтобы имело место равенство трех чисел 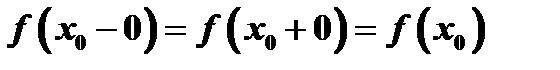 .
.
Если существуют односторонние пределы, но нарушено какое-либо из этих равенств, то 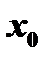 называется точкой разрыва первого рода функции
называется точкой разрыва первого рода функции 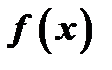 .
.
Если хотя бы один из односторонних пределов не существует (в частности, равен 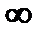 , то
, то 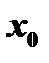 называется точкой разрыва второго рода функции
называется точкой разрыва второго рода функции 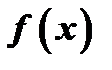 .
.
Непрерывные функции обладают следующими свойствами:
Теорема 1. Сумма, разность, произведение и частное двух функций, непрерывных в точке 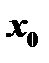 , также являются функциями, непрерывными в точке
, также являются функциями, непрерывными в точке 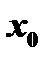 (в случае частного предполагается, что знаменатель не обращается в нуль в этой точке).
(в случае частного предполагается, что знаменатель не обращается в нуль в этой точке).
Теорема 2. Все основные элементарные функции непрерывны там, где они определены.
Теорема 3. Сложная функция, составленная из непрерывных функций, непрерывна.
Теорема 4. (Теорема Вейерштрасса). Функция 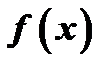 , непрерывная в замкнутом промежутке
, непрерывная в замкнутом промежутке 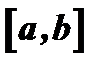 , достигает в этом промежутке своего наибольшего и своего наименьшего значений, т.е. существуют такие точки
, достигает в этом промежутке своего наибольшего и своего наименьшего значений, т.е. существуют такие точки 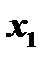 и
и 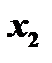 промежутка
промежутка 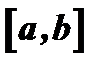 , что
, что 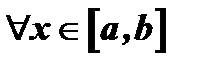 выполняются неравенства
выполняются неравенства 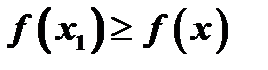 и
и 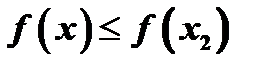 .
.
Дата добавления: 2016-06-05; просмотров: 1835;











