Основные теоремы дифференциального исчисления
Теорема Ферма. Если функция 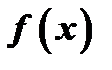 определена в некотором промежутке
определена в некотором промежутке 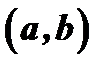 , достигает в некоторой внутренней точке
, достигает в некоторой внутренней точке  этого промежутка наибольшего (или наименьшего) значения, существует конечная производная
этого промежутка наибольшего (или наименьшего) значения, существует конечная производная 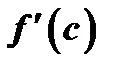 , то
, то 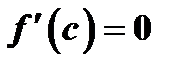 .
.
 Доказательство. По условию в точке
Доказательство. По условию в точке  функция
функция 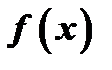 достигает, допустим, наибольшего значения, что означает
достигает, допустим, наибольшего значения, что означает 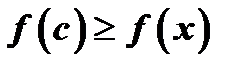 , т.е.
, т.е. 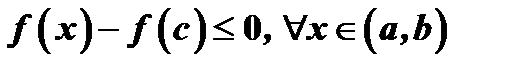 .
.
Пусть  . Тогда
. Тогда 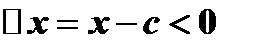 и
и 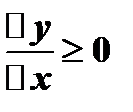 . По условию в точке
. По условию в точке 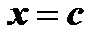 существует конечная производная, следовательно,
существует конечная производная, следовательно,
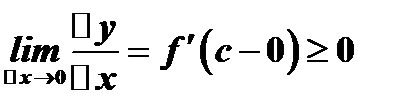 .
.
Пусть  .
. 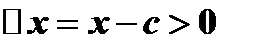 и
и 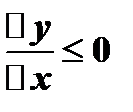 , следовательно,
, следовательно, 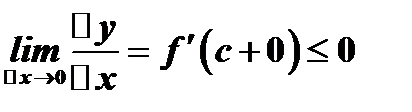 .
.
Сопоставляя неравенства 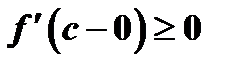 и
и 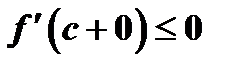 , заключаем, что
, заключаем, что 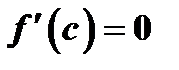 .
.
Геометрический смысл заключения теоремы состоит в том, что касательная к графику функции 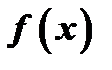 в точке
в точке 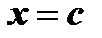 параллельна оси абсцисс (рис. 5).
параллельна оси абсцисс (рис. 5).
Теорема Ролля. Если функция 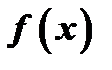 непрерывна в замкнутом промежутке
непрерывна в замкнутом промежутке 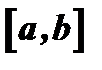 , дифференцируема по крайней мере в открытом промежутке
, дифференцируема по крайней мере в открытом промежутке 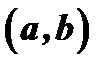 , принимает на концах промежутка равные значения
, принимает на концах промежутка равные значения 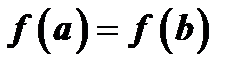 , то внутри промежутка
, то внутри промежутка 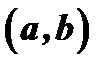 существует точка
существует точка 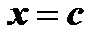 такая, что
такая, что 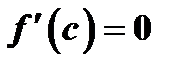 .
.
 Доказательство. По теореме Вейерштрасса непрерывная функция в замкнутом промежутке достигает своего наибольшего значения
Доказательство. По теореме Вейерштрасса непрерывная функция в замкнутом промежутке достигает своего наибольшего значения 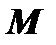 и своего наименьшего значения
и своего наименьшего значения 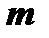 . Пусть
. Пусть 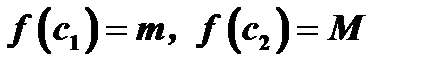 , где
, где 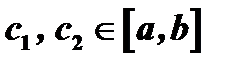 . Возможны только два случая:
. Возможны только два случая:
1) Обе точки совпадают с концами промежутка 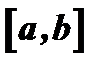 . Тогда из третьего условия теоремы следует, что
. Тогда из третьего условия теоремы следует, что 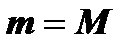 и что функция постоянна в
и что функция постоянна в 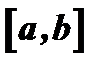 . Следовательно, в любой точке этого промежутка
. Следовательно, в любой точке этого промежутка 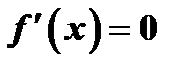 .
.
2) Хотя бы одна из точек 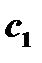 или
или 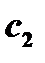 не совпадает ни с одним из концов промежутка
не совпадает ни с одним из концов промежутка 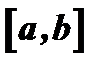 . Обозначим эту точку
. Обозначим эту точку  . Она находится внутри промежутка
. Она находится внутри промежутка 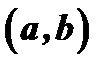 и в ней функция достигает наибольшего или наименьшего значения. Кроме того, в точке
и в ней функция достигает наибольшего или наименьшего значения. Кроме того, в точке  существует производная функции. Согласно теореме Ферма в этой точке
существует производная функции. Согласно теореме Ферма в этой точке 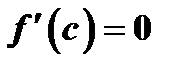 .
.
Геометрическое содержание теоремы Ролля состоит в том, что если выполнены условия теоремы, то внутри промежутка 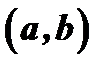 существует хотя бы одна точка, в которой касательная к графику функции параллельна оси абсцисс (рис. 6).
существует хотя бы одна точка, в которой касательная к графику функции параллельна оси абсцисс (рис. 6).
Теорема Лагранжа. Если функция 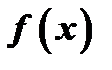 непрерывна в замкнутом промежутке
непрерывна в замкнутом промежутке 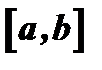 , дифференцируема по крайней мере в открытом промежутке
, дифференцируема по крайней мере в открытом промежутке 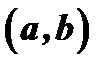 , то внутри промежутка
, то внутри промежутка 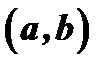 существует точка
существует точка 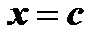 такая, что выполняется равенство
такая, что выполняется равенство
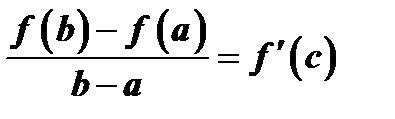 .
.
 Доказательство. Рассмотрим вспомогательную функцию
Доказательство. Рассмотрим вспомогательную функцию 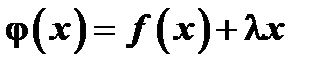 . Функция
. Функция 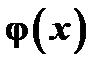 удовлетворяет первым двум условиям теоремы Ролля при любом
удовлетворяет первым двум условиям теоремы Ролля при любом  , как сумма двух непрерывных и дифференцируемых функций
, как сумма двух непрерывных и дифференцируемых функций 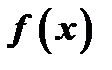 и
и 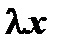 . Она удовлетворяет третьему условию теоремы Ролля
. Она удовлетворяет третьему условию теоремы Ролля 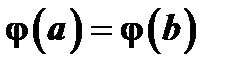 при специальном выборе числа
при специальном выборе числа 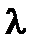 из условия
из условия 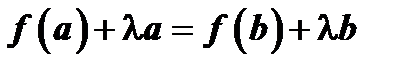 , т.е. если
, т.е. если 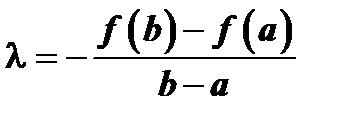 . При таком
. При таком  функция
функция  удовлетворяет всем условиям теоремы Ролля, а поэтому в силу эаключения этой теоремы внутри промежутка
удовлетворяет всем условиям теоремы Ролля, а поэтому в силу эаключения этой теоремы внутри промежутка 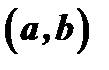 существует значение
существует значение  , при котором
, при котором 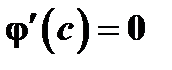 . Последнее равенство можно записать в виде
. Последнее равенство можно записать в виде 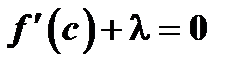 или
или 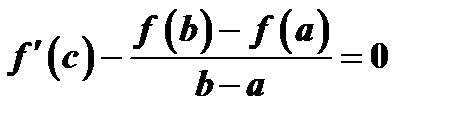 . Откуда
. Откуда 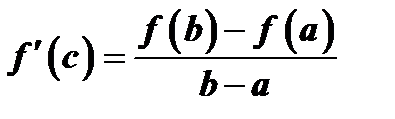 .
.
Выведенная формула называется формулой Лагранжа, или формулой конечных приращений. Из нее непосредственно следует соотношение
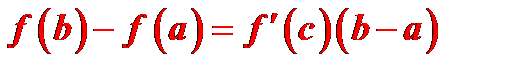
Теорема Коши. Если функции 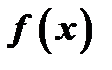 и
и 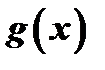 непрерывны в замкнутом промежутке
непрерывны в замкнутом промежутке 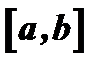 , дифференцируемы по крайней мере в открытом промежутке
, дифференцируемы по крайней мере в открытом промежутке 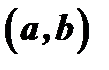 ,
, 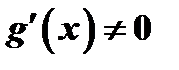 в промежутке
в промежутке 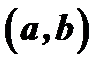 , то внутри
, то внутри 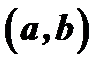 существует значение
существует значение  такое, что имеет место равенство
такое, что имеет место равенство 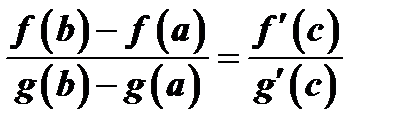 .
.
Доказательство. Из третьего условия теоремы следует, что 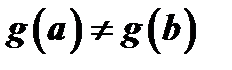 , в чем можно убедиться рассуждением от противного. В самом деле, если
, в чем можно убедиться рассуждением от противного. В самом деле, если 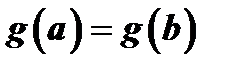 , то, по теореме Ролля, примененной к функции
, то, по теореме Ролля, примененной к функции 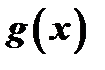 (здесь выполнены все условия теоремы Ролля), получается, что
(здесь выполнены все условия теоремы Ролля), получается, что 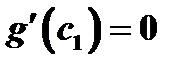 в некоторой внутренней точке
в некоторой внутренней точке 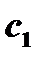 промежутка
промежутка 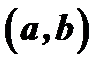 . Но это противоречит третьему условию теоремы.
. Но это противоречит третьему условию теоремы.
Рассмотрим вспомогательную функцию 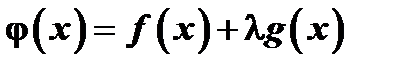 , где
, где 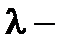 число. Функция
число. Функция 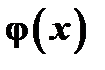 удовлетворяет первым двум условиям теоремы Ролля при любом
удовлетворяет первым двум условиям теоремы Ролля при любом 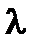 как сумма двух непрерывных и дифференцируемых функций. Она будет удовлетворять и третьему условию теоремы Ролля, если выбрать
как сумма двух непрерывных и дифференцируемых функций. Она будет удовлетворять и третьему условию теоремы Ролля, если выбрать 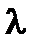 такой, чтобы
такой, чтобы 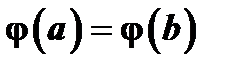 , т.е.
, т.е. 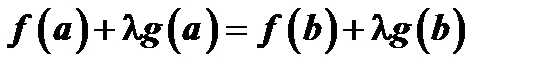 , откуда
, откуда 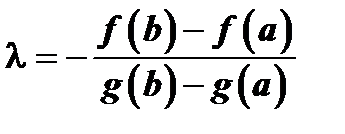 . Поэтому в силу заключения этой теоремы существует внутри
. Поэтому в силу заключения этой теоремы существует внутри 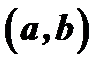 число
число  такое, что имеет место равенство
такое, что имеет место равенство 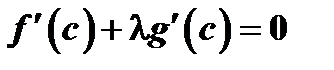 , или
, или 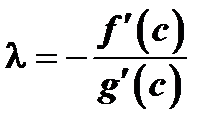 . Следовательно,
. Следовательно, 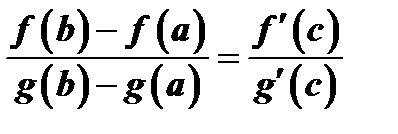 .
.
Заметим, что теорема Лагранжа есть частный случай теоремы Коши, соответствующий случаю 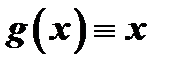 .
.
.Раскрытие неопределенностей 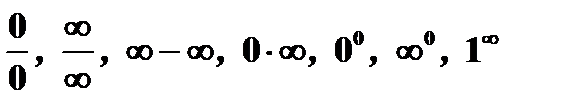
 Пусть функции
Пусть функции 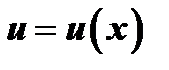 и
и 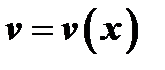 определены в окрестности некоторой точки
определены в окрестности некоторой точки 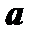 .
.
Рассмотрим при 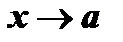 следующие выражения:
следующие выражения: 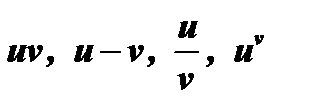 .
.
Условимся в следующем. Назовем
1) неопределенностью вида 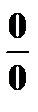 отношение
отношение 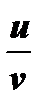 двух бесконечно малых (случай
двух бесконечно малых (случай 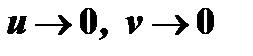 ),
),
2) неопределенностью вида 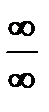 отношение
отношение 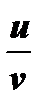 двух бесконечно больших (случай
двух бесконечно больших (случай 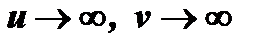 ),
),
3) неопределенностью вида 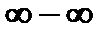 разность
разность 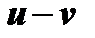 двух бесконечно больших одного знака (случай
двух бесконечно больших одного знака (случай 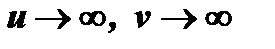 ),
),
4) неопределенностью вида 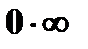 произведение
произведение 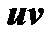 бесконечно малой на бесконечно большую (случай
бесконечно малой на бесконечно большую (случай 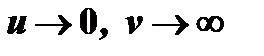 ),
),
5) неопределенностью  выражение
выражение 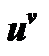 (случай
(случай 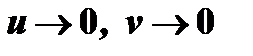 ),
),
6) неопределенностью 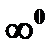 выражение
выражение 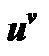 (случай
(случай 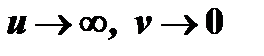 ),
),
7) неопределенностью 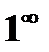 выражение
выражение 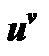 (случай
(случай 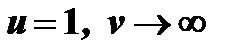 ).
).
Раскрыть неопределенность того или иного вида – это значит найти предел соответствующей функции.
Рассмотрим прежде всего случай отношения бесконечно малых.
Теорема Лопиталя. Предел отношения двух бесконечно малых существует и равен пределу отношения их производных:
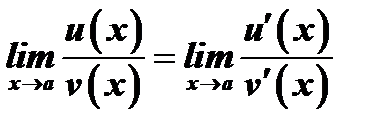
(в этом состоит так называемое правило Лопиталя), если выполнены следующие условия: 1) функции 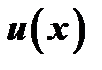 и
и 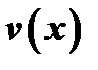 определены и дифференцируемы в некоторой окрестности
определены и дифференцируемы в некоторой окрестности 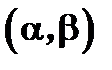 точки
точки 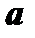 и
и 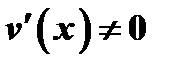 в
в 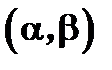 ; 2)
; 2) 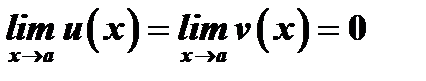 ; 3) существует предел
; 3) существует предел 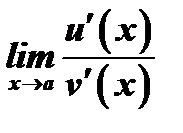 .
.
Доказательство. Приведем доказательство теоремы для случая, когда 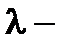 число. Функции
число. Функции 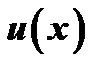 и
и 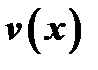 удовлетворяют всем условиям теоремы Коши в промежутке между
удовлетворяют всем условиям теоремы Коши в промежутке между 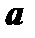 и
и 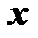 , где
, где 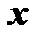 фиксировано в
фиксировано в 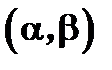 . Поэтому внутри этого промежутка существует такое число
. Поэтому внутри этого промежутка существует такое число  , что
, что 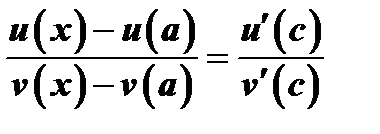 и
и 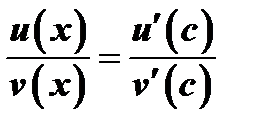 , т.к. согласно непрерывности
, т.к. согласно непрерывности 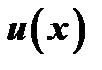 и
и 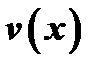 в точке
в точке 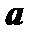 и второго условия теоремы, имеем
и второго условия теоремы, имеем 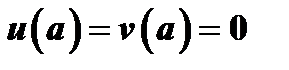 .
.
При 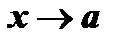 переменная
переменная  , заключенная между
, заключенная между 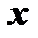 и
и 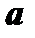 , тоже стремится к
, тоже стремится к 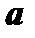 . При этом в силу третьего условия теоремы существует предел отношения функций и он равен
. При этом в силу третьего условия теоремы существует предел отношения функций и он равен
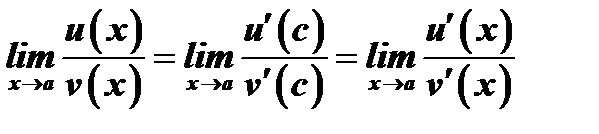
Сформулируем теорему, относящуюся к случаю неопределенности вида 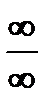 .
.
Теорема. Если 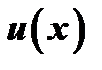 и
и 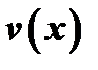 определены и дифференцируемы при всех
определены и дифференцируемы при всех 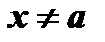 в окрестности точки
в окрестности точки 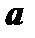 , где
, где 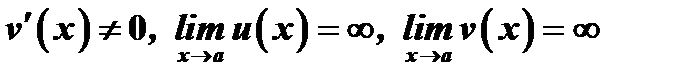 , существует предел
, существует предел 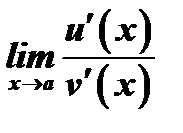 , то существует предел отношения
, то существует предел отношения 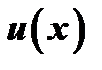 к
к 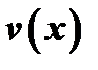 и он равен пределу отношения производных этих функций
и он равен пределу отношения производных этих функций 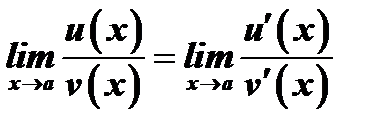 .
.
Н е о п р е д е л е н н о с т ь в и д а 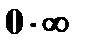 приводится к неопределенности вида
приводится к неопределенности вида 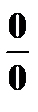 или
или 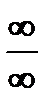 путем преобразования произведения функций
путем преобразования произведения функций 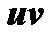 к виду отношения
к виду отношения 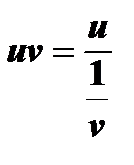 или
или 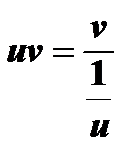 .
.
Н е о п р е д е л е н н о с т ь в и д а 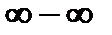 можно привести к неопределенности вида
можно привести к неопределенности вида 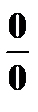 путем представления разности
путем представления разности 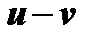 в виде отношения
в виде отношения
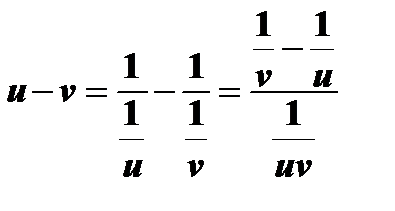
Н е о п р е д е л е н н о с т ь в и д а 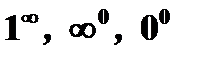 можно раскрыть с помощью тождества
можно раскрыть с помощью тождества 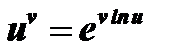 , которое имеет место при условии
, которое имеет место при условии 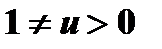 .
.
Дата добавления: 2016-06-05; просмотров: 2209;











