Функции нескольких переменных

Пусть 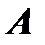есть область изменения независимых переменных 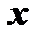и .

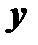Переменная 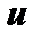называется функцией независимых переменных 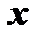и 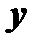на множестве 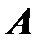, если каждой паре чисел 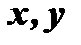из 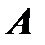соответствует определенное значение 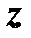. Переменные 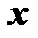и 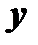называются аргументами функции .

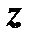Множество 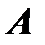пар чисел 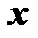, , 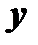на котором определена функция, называется областью определения.

Функция 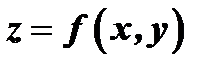называется непрерывной функцией в точке 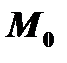, если выполнено условие 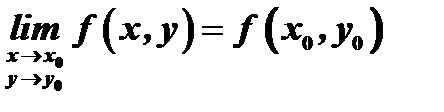. Функция 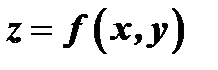называется непрерывной в области, если она непрерывна в каждой точке этой области.

Рассмотрим произвольную точку 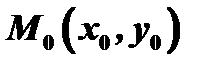области 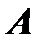. Если переменная сохраняет постоянное значение 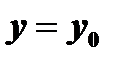, то переменная 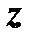становится функцией одной независимой переменной 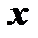, именно 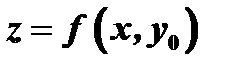. Найдем производную функции 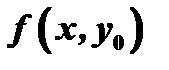в точке 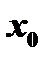. Для этого дадим 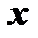приращение 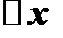, функция получит приращение

,

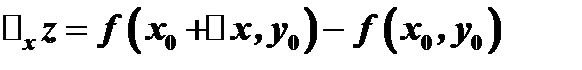называемое частным приращением функции 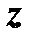по переменной .

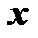Определение. Частной производной функции 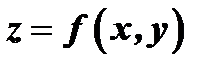по переменной 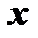в точке 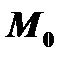называется предел (если он существует) отношения соответствующего частного приращения функции 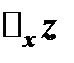к вызвавшему его приращению независимой переменной 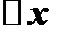, когда 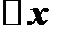стремится к нулю: 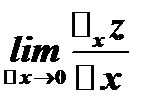и обозначается .

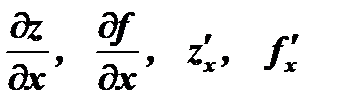Аналогично определяется частная производная функции по переменной :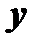

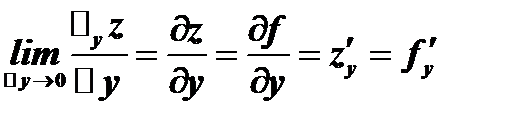
Выражение 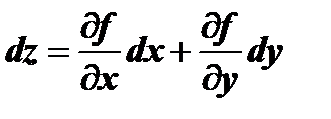называется полным дифференциалом.

Предположим, что в уравнени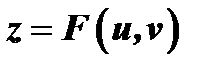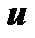и и 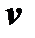являются функциями независимых переменных 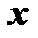и 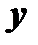. В этом случае 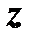есть сложная функция от аргументов 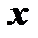и 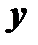, тогда

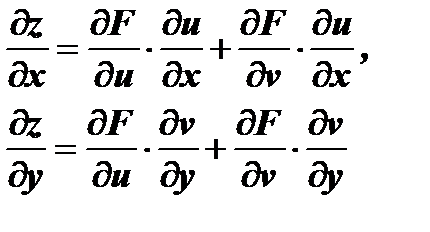
Если задана функция 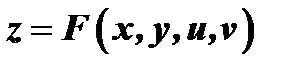, где 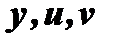в свою очередь зависят от одного аргумента 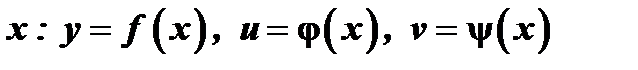, то, по сути дела, 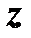является функцией только одной переменной 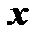и можно ставить вопрос о нахождении производной 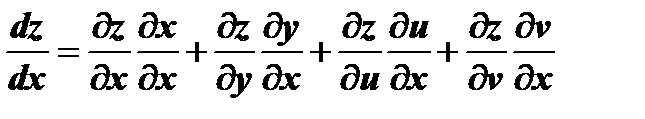; но т.к. 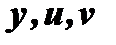- функции только одного 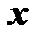, то частные производные обращаются в обыкновенные; кроме того, 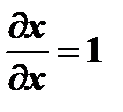; поэтому

.

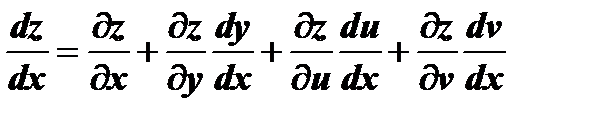Пусть имеем функцию двух переменных: 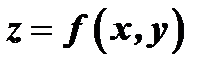. Частные производные 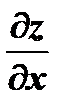и 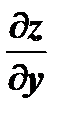, вообще говоря, являются функциями переменных 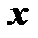и 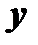. Поэтому от них можно снова находить частные производные. Следовательно, частных производных второго порядка от функции двух переменных четыре, т.к. каждую из функци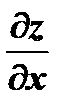й и 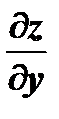можно дифференцировать как по 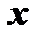, так и по 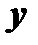. Вторые частные производные обозначают так:

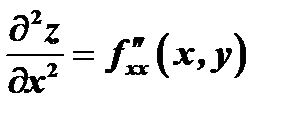, здесь 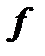дифференцируется последовательно два раза по ;

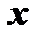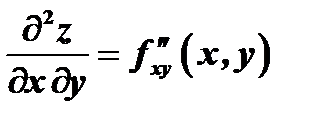, здесь 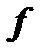дифференцируется по 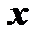, а потом результат дифференцируется по ;

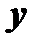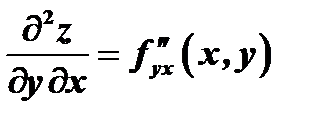, здесь 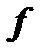дифференцируется по 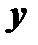, а потом результат дифференцируется по ;

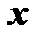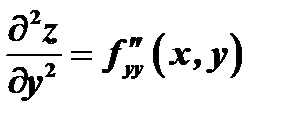, здесь 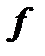дифференцируется последовательно два раза по .

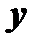Заметим, что .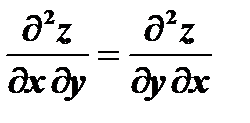

1.