Расстояние точки от плоскости
Даны нормальное уравнение плоскости 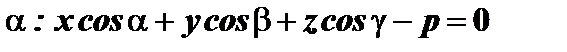 и точка
и точка 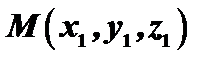 . Требуется найти расстояние точки
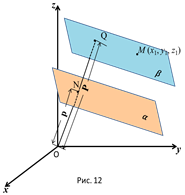
. Требуется найти расстояние точки 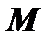 до плоскости 𝛼 (рис. 12).
до плоскости 𝛼 (рис. 12).
 Проведём через точку
Проведём через точку 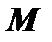 плоскость
плоскость 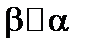 , уравнение которой в нормальной форме будет иметь вид:
, уравнение которой в нормальной форме будет иметь вид:
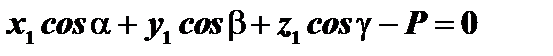 ,
,
где 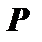 - расстояние плоскости
- расстояние плоскости 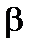 от начала координат.
от начала координат.
Условимся называть отклонением данной точки от данной плоскости число d, равное длине перпендикуляра, опущенного из этой точки на плоскость, взятой со знаком +, если точка и начало координат лежат по разные стороны от данной плоскости, и со знаком -, если они лежат по одну сторону от плоскости; для точек, лежащих на плоскости, отклонение равно нулю. Ясно, что расстояние от данной точки до плоскости равно абсолютной величине отклонения.
Из рисунка 12 видно, что искомое расстояние 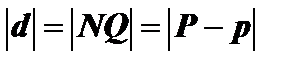 , но из уравнения плоскости
, но из уравнения плоскости 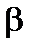 имеем:
имеем:
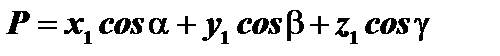 ,
,
следовательно,
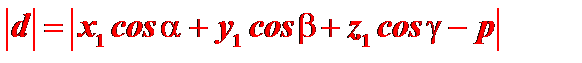 (14)
(14)
Таким образом, чтобы вычислить расстояние точки от плоскости, нужно в левую часть нормального уравнения плоскости подставить координаты заданной точки и взять абсолютную величину полученного результата.
Прямая линия. Различные виды уравнения прямой
Дата добавления: 2016-06-05; просмотров: 1885;











