Смешанное произведение трех векторов
Дана упорядоченная тройка ненулевых векторов 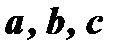 . Если перемножить
. Если перемножить 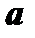 на
на 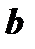 векторно и полученный результат
векторно и полученный результат 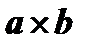 умножить на вектор
умножить на вектор  скалярно, то получим число v, которое называется векторно-скалярным, или смешанным, произведением векторов
скалярно, то получим число v, которое называется векторно-скалярным, или смешанным, произведением векторов 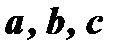 и обозначается символом
и обозначается символом 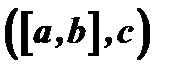 или
или 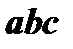 ;
;
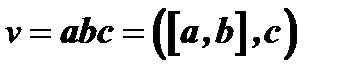
Смешанное произведение векторов обладает следующими свойствами:
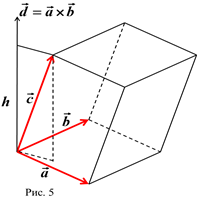
1. Для того, чтобы выяснить геометрический смысл смешанного произведения, построим параллелепипед на векторах 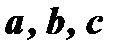 , приведя их к общему началу (рис.5). Обозначим
, приведя их к общему началу (рис.5). Обозначим 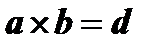 ; длина вектора
; длина вектора 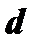 численно равна площади параллелограмма, построенного на векторах
численно равна площади параллелограмма, построенного на векторах 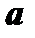 и
и 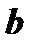 . Смешанное произведение равно
. Смешанное произведение равно 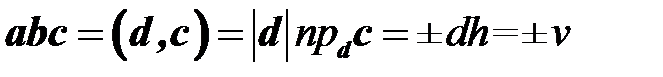 , где
, где 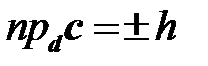 , а
, а 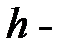 высота параллелепипеда. Заметим, что получается
высота параллелепипеда. Заметим, что получается 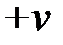 , если угол
, если угол 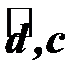 острый, и
острый, и 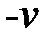 , если угол
, если угол 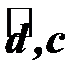 тупой. Таким образом, установлено: смешанное произведение трех векторов численно равно объему параллелепипеда, построенного на векторах
тупой. Таким образом, установлено: смешанное произведение трех векторов численно равно объему параллелепипеда, построенного на векторах 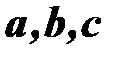 , приведенных к общему началу, взятому со знаком «плюс», если
, приведенных к общему началу, взятому со знаком «плюс», если 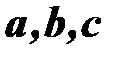 образуют тройку векторов, одноименную с основной (т.е. правую), и со знаком «минус» в противном случае.
образуют тройку векторов, одноименную с основной (т.е. правую), и со знаком «минус» в противном случае.
2. Смешанное произведение не меняется при круговой перестановке сомножителей 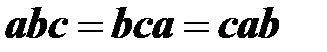 , т.к. при этом получаются равновеликие параллелепипеды, ребра которых сохраняют взаимную ориентацию.
, т.к. при этом получаются равновеликие параллелепипеды, ребра которых сохраняют взаимную ориентацию.
3. Смешанное произведение меняет знак при перестановке любых двух сомножителей, например, 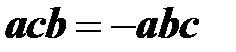 , т.к. при этом получаются равновеликие параллелепипеды, но ориентация ребер меняется.
, т.к. при этом получаются равновеликие параллелепипеды, но ориентация ребер меняется.
Три вектора называются компланарными, если будучи приведенными к общему началу они лежат в одной плоскости.
4. Смешанное произведение трех векторов равно нулю тогда и только тогда, когда сомножители компланарны.
Пусть вектора заданы своими проекциями на координатные оси:
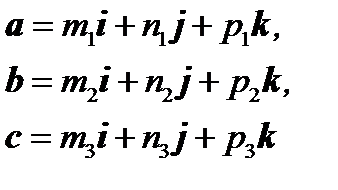
Составим смешанное произведение 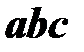 . Для этого умножим
. Для этого умножим 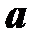 на
на 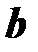 векторно:
векторно: 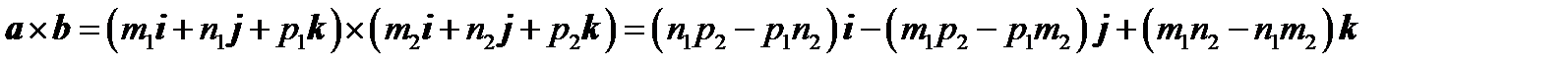
Теперь найдем скалярное произведение вектора 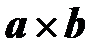 и
и 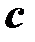 , как сумма произведений одноименных координат:
, как сумма произведений одноименных координат:
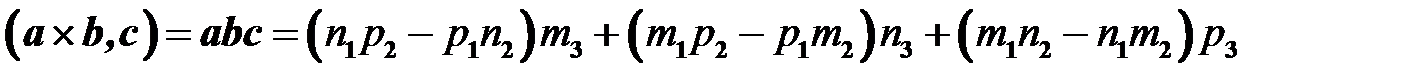
Правую часть этого равенства можно рассматривать как разложение написанного ниже определителя по элементам последней строки. Поэтому имеем
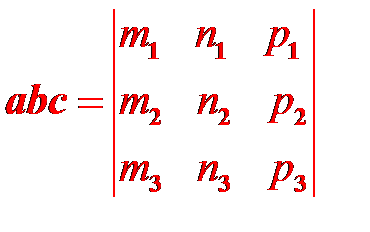
Из геометрического смысла смешанного произведения следует, что векторы 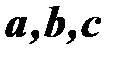 компланарны тогда и только тогда, когда равно нулю их смешанное произведение. Таким образом, заключаем, что условие
компланарны тогда и только тогда, когда равно нулю их смешанное произведение. Таким образом, заключаем, что условие
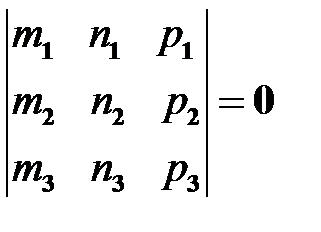
необходимо и достаточно для компланарности векторов 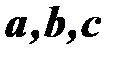 .
.
Дата добавления: 2016-06-05; просмотров: 2273;











