Общее уравнение плоскости
Теорема.Любая плоскость имеет своим уравнением в декартовых координатах уравнение вида 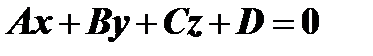 , где
, где 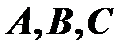 - постоянные. И обратно, если постоянные не равны нулю одновременно, то существует плоскость, для которой уравнение
- постоянные. И обратно, если постоянные не равны нулю одновременно, то существует плоскость, для которой уравнение 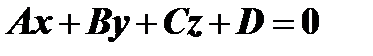 является её уравнением ( в декартовых координатах ).
является её уравнением ( в декартовых координатах ).

Доказательство. 1. Пусть 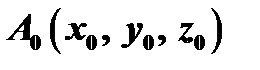 - какая-нибудь точка плоскости и
- какая-нибудь точка плоскости и 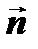 - ненулевой вектор, перпендикулярный плоскости. Тогда, какова бы ни была точка
- ненулевой вектор, перпендикулярный плоскости. Тогда, какова бы ни была точка 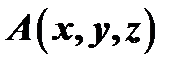 плоскости векторы
плоскости векторы 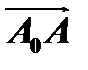 и
и 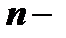 перпендикулярны (рис. 5). Необходимым и достаточным условием перпендикулярности двух векторов является равенство нулю их скалярного произведения т.е.
перпендикулярны (рис. 5). Необходимым и достаточным условием перпендикулярности двух векторов является равенство нулю их скалярного произведения т.е. 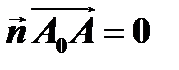 . Пусть
. Пусть 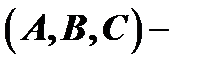 координаты вектора
координаты вектора 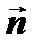 . Так как вектор
. Так как вектор 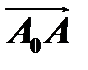 имеет координаты
имеет координаты 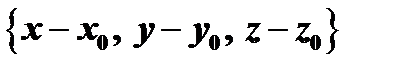 , то
, то
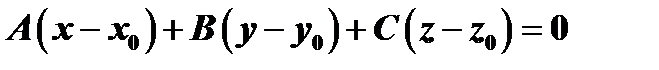 или
или
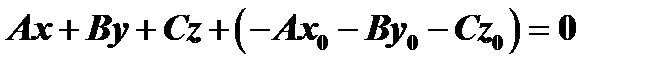 .
.
Обозначив 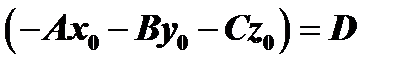 , получим
, получим 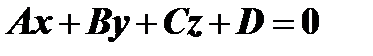 . Первая часть теоремы доказана.
. Первая часть теоремы доказана.
2. Пусть 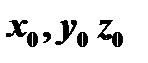 - какое-нибудь решение уравнения
- какое-нибудь решение уравнения 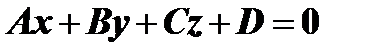 . Тогда, подставив
. Тогда, подставив 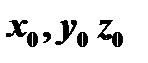 вместо
вместо 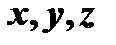 получим
получим 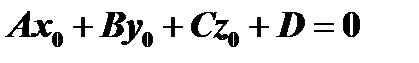 , откуда
, откуда 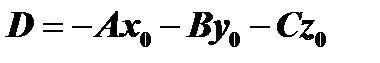 , и уравнение
, и уравнение 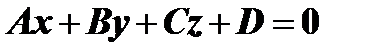 можно переписать в виде
можно переписать в виде 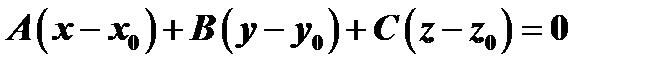 , или, в векторной форме
, или, в векторной форме 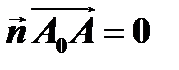 . Отсюда следует, что все точки плоскости, проходящей через точку
. Отсюда следует, что все точки плоскости, проходящей через точку 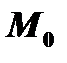 , перпендикулярно вектору
, перпендикулярно вектору 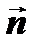 , удовлетворяют уравнению
, удовлетворяют уравнению 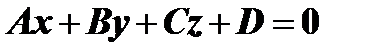 и, следовательно, оно является уравнением этой плоскости.
и, следовательно, оно является уравнением этой плоскости.
Вектор 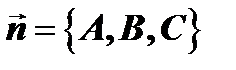 , перпендикулярный плоскости, называется нормальным вектором плоскости.
, перпендикулярный плоскости, называется нормальным вектором плоскости.
Уравнение
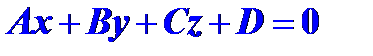 (3)
(3)
называется общим уравнением плоскости. Коэффициенты при 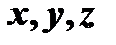 в этом уравнении представляют координаты её нормального вектора в базисе
в этом уравнении представляют координаты её нормального вектора в базисе 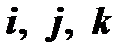 .
.
Дата добавления: 2016-06-05; просмотров: 1650;











