Пересечение прямой и плоскости

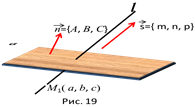Пусть даны уравнения прямой линии:

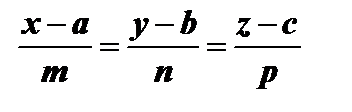
и уравнение плоскости:

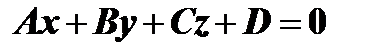
Координаты точки пересечения прямой линии с плоскостью должны одновременно удовлетворять и урав-нениям прямой и уравнению плоскости. Другими словами нужно совместно решить уравнения 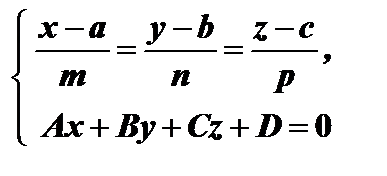Представив уравнения прямой в параметрической форме:

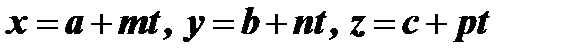
и подставив эти значения во второе уравнение, получим:

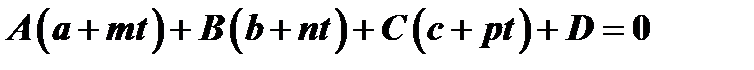или

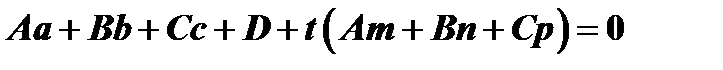, откуда находим:

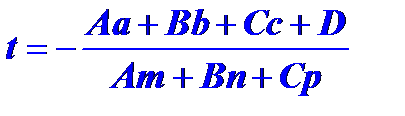(25)

Подставив значение в параметрические уравнения прямой линии получим координаты точки пересечения прямой и плоскости.

Проведём анализ полученной формулы (25):

1) если 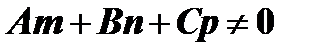, то , вычисленное по формуле (25), имеет определённое конечное значение. Следовательно, в этом случае прямая пересекает плоскость в одной точке;

2) если 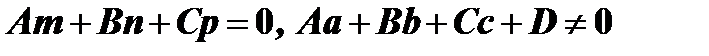, то, в силу первого равенства прямая параллельна плоскости, в силу второго неравенства, точка (a, b, c), через которую проходит прямая, не принадлежит плоскости. Следовательно, прямая не имеет ни одной общей точки с плоскостью;

3) если 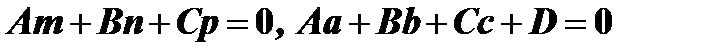, то, в силу первого равенства прямая параллельна плоскости и в силу второго равенства точка (a, b, c), через которую проходит прямая, принадлежит плоскости. Следовательно, прямая вся лежит в плоскости.