Декартовы координаты в пространстве

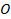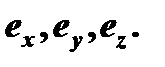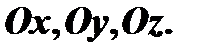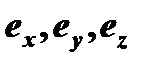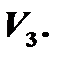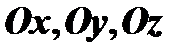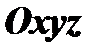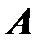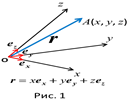
Проведём из некоторой точки пространства три прямые, не лежащие в одной плоскости и поместим на каждой из них соответственно единичные векторы Обозначим прямые через Векторы , очевидно, образуют базис пространства Прямые называются осями координат. Пусть в пространстве введена общая система декартовых координат с координатным базисом Возьмём произвольную точку пространства, она определяет некоторый вектор 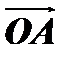(рис. 1). Вектор, начало которого совпадает с началом координат, а конец – с некоторой точкой 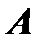, называется радиус-вектором точки 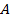. Согласно 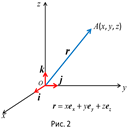разделу векторной алгебры имеем 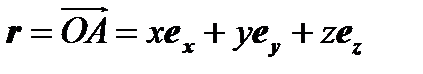,где 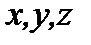– координаты вектора 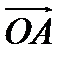в базисе . Координаты точки будем записывать в круглых скобках рядом с буквой, которой обозначена сама точка .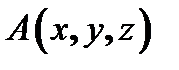

Если оси координат взаимно перпендикулярны и векторы - единичные, то система координат 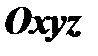называется прямоугольной декартовой системой координат в пространстве. При этом единичные векторы осей прямоугольной декартовой системы координат называются ортами и обозначаются

.

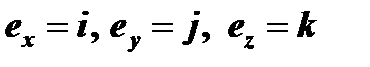Координаты вектора в базисе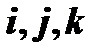являются его проекциями на соответствующие векторы базиса, т.е.

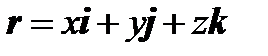(1)