Скалярное произведение двух векторов
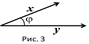 Углом между векторами
Углом между векторами 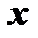 и
и 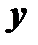 называется угол
называется угол 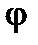 , на который следует повернуть один из векторов, для того чтобы их направления совпали (рис.3).
, на который следует повернуть один из векторов, для того чтобы их направления совпали (рис.3).
Условимся в дальнейшем под углом между двумя векторами понимать угол 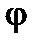 , удовлетворяющий условию
, удовлетворяющий условию 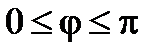 .
.
Скалярным произведением векторов 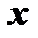 и
и 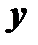 называется число, равное произведению модулей этих векторов на косинус угла между ними и обозначается
называется число, равное произведению модулей этих векторов на косинус угла между ними и обозначается 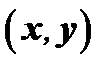 или
или 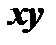 , таким образом
, таким образом
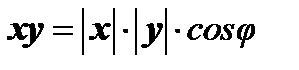 (6)
(6)
Теорема 1. Для того, чтобы два вектора были ортогональны, необходимо и достаточно, чтобы их скалярное произведение равнялось нулю.
Доказательство. 1. Необходимость. Пусть векторы 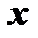 и
и 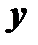 ортогональны, т.е.
ортогональны, т.е. 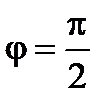 . Тогда
. Тогда 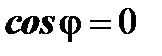 , и согласно формуле (6) скалярное произведение
, и согласно формуле (6) скалярное произведение 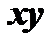 равно нулю.
равно нулю.
2. Достаточность. Пусть 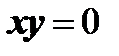 . Если один из векторов является нулевым, то утверждение доказано, т.к. нулевой вектор имеет неопределенное направление и его можно считать ортогональным любому вектору. Если же
. Если один из векторов является нулевым, то утверждение доказано, т.к. нулевой вектор имеет неопределенное направление и его можно считать ортогональным любому вектору. Если же 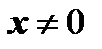 и
и 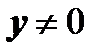 , то
, то 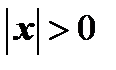 и
и 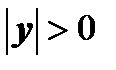 . Тогда из формулы (6) и условия
. Тогда из формулы (6) и условия 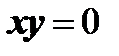 следует, что
следует, что 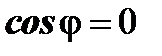 . Значит
. Значит 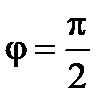 , т.е. векторы
, т.е. векторы 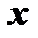 и
и 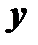 ортогональны.
ортогональны.
Скалярное произведение обладает следующими свойствами:
1) 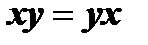 ;
;
2) 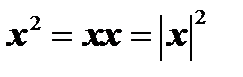 ;
;
3) Скалярное произведение двух векторов равно модулю одного из них, умноженному на проекцию второго вектора на первый, т.е.
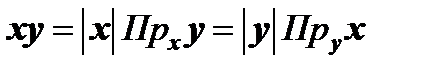 ;
;
4) 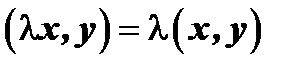 ;
;
5) 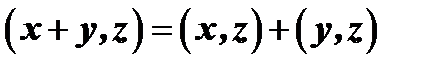
Пусть даны два вектора, разложенные по базису 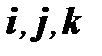 :
:
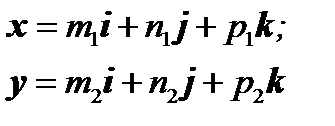 .
.
Найдем 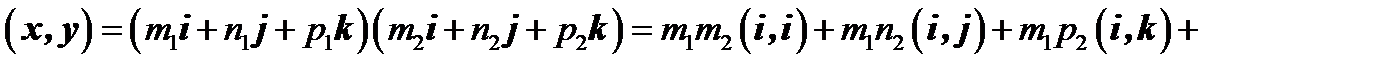
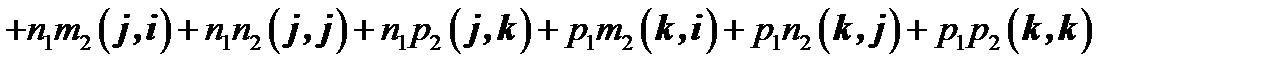 . Принимая во внимание, что базис ортонормированный, т.е.
. Принимая во внимание, что базис ортонормированный, т.е. 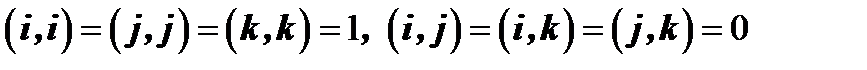 , получим
, получим 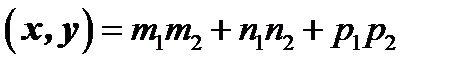 . Таким образом, скалярное произведение двух векторов, заданных координатами равно сумме произведений одноименных координат, т.е.
. Таким образом, скалярное произведение двух векторов, заданных координатами равно сумме произведений одноименных координат, т.е.
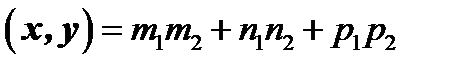 ( 7 ).
( 7 ).
Необходимым и достаточным условием перпендикулярности двух векторов, заданных координатами является:
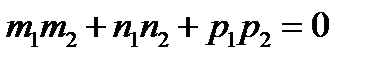 ( 8 )
( 8 )
Из формулы (6) получим формулу для косинуса угла между векторами 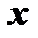 и
и 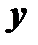 :
:
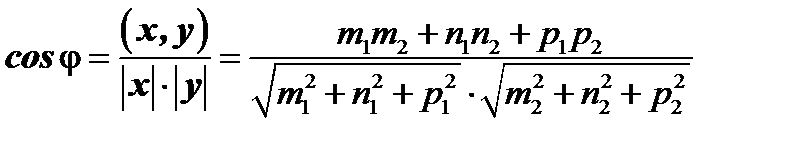 ( 9 )
( 9 )
Дата добавления: 2016-06-05; просмотров: 2593;











