Векторы и линейные операции над ними
Величины, с которыми приходится иметь дело в физике, электротехнике, механике и других прикладных науках, разделяются на два вида. Одни из них вполне определяются числом, которое выражает отношение этой величины к соответствующей единице измерения, и называются скалярными величинами; другие же определяются не только числом, но еще и направлением в пространстве, и называются векторными. Примерами скалярных величин являются такие величины как длина отрезка, площадь фигуры, объем тела, масса тела, плотность и другие; примерами векторных величин – сила, скорость, ускорение и т.д.
Скалярные величины характеризуются числами, а векторные – векторами.
 Вектор представляет собой геометрический объект, характеризуемый длиной и направлением. Вектор обозначается:
Вектор представляет собой геометрический объект, характеризуемый длиной и направлением. Вектор обозначается: 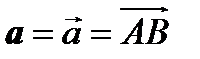 .
. 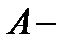 начало вектора,
начало вектора, 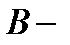 конец вектора. Расстояние между точками, составляющими вектор, называется модулем вектора и обозначается
конец вектора. Расстояние между точками, составляющими вектор, называется модулем вектора и обозначается 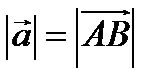 . Векторы, лежащие на параллельных прямых называются коллинеарными. Векторы, параллельные одной и той же плоскости, называются компланарными. Вектор, модуль которого равен единице, называется единичным.
. Векторы, лежащие на параллельных прямых называются коллинеарными. Векторы, параллельные одной и той же плоскости, называются компланарными. Вектор, модуль которого равен единице, называется единичным.
Алгебраической суммой двух векторов 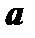 и
и 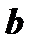 называется вектор
называется вектор 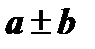 , который получается из векторов
, который получается из векторов 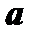 и
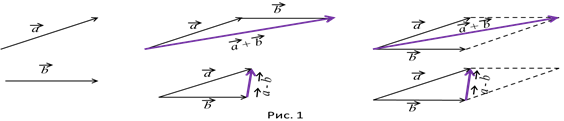
и 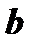 или равных им векторов согласно рис.1.
или равных им векторов согласно рис.1.
 Произведением вектора
Произведением вектора 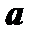 на число
на число 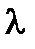 называется вектор
называется вектор 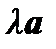 , модуль которого равен произведению модуля вектора
, модуль которого равен произведению модуля вектора 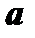 на модуль числа
на модуль числа 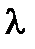 , а направление совпадает с направлением вектора
, а направление совпадает с направлением вектора 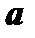 , если
, если 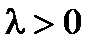 , и противоположно направлению вектора
, и противоположно направлению вектора 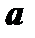 , если
, если 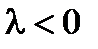 .
.
Дата добавления: 2016-06-05; просмотров: 1803;











