О п р е д е л и т е л и

Пусть дана квадратная матрица второго порядка 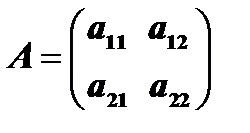. Определителем второго порядка, соответствующим матрице 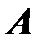, называется число, определяемое равенством 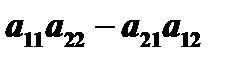и обозначается

.

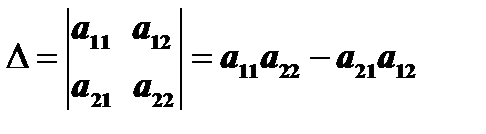Схема вычисления определителя второго порядка

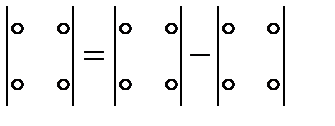
Рассмотрим квадратную матрицу третьего порядка 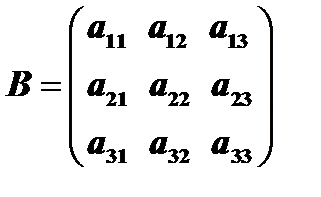. Определителем третьего порядка, соответствующим матрице 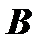называется число, определяемое равенством 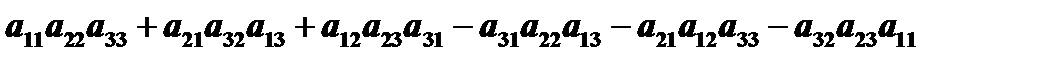и обозначается

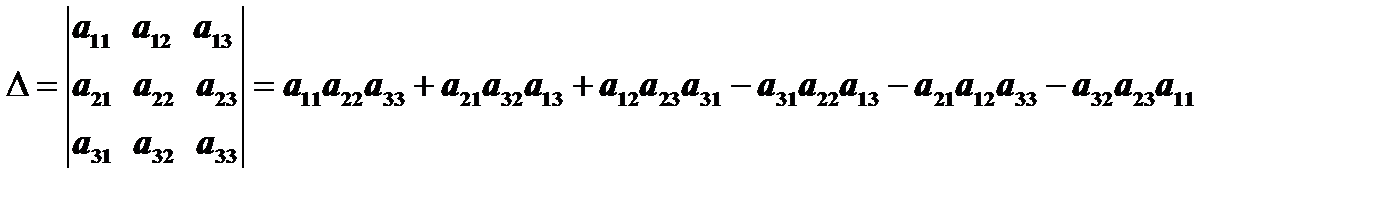
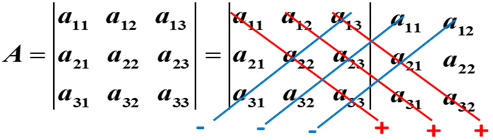
Схема вычисления определителя третьего порядка

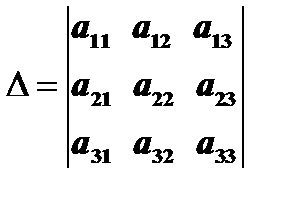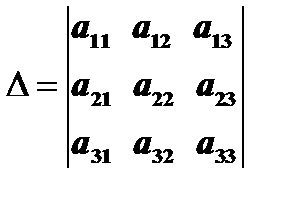Если из определителя вычеркнуть одну строку и один столбец, на пересечении которых стоит некоторый элемент, то получится определитель второго порядка, который называется миноромопределителя , соответствующим этому элементу. Так, например, если из определителя вычеркнуть вторую строку и третий столбец 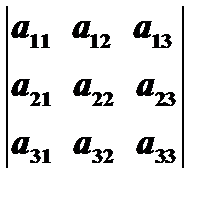, то минором элемента 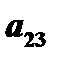будет определитель второго порядка 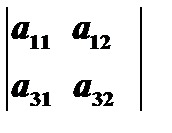и обозначается 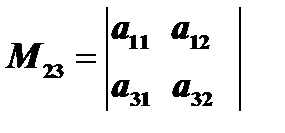. Условимся называть алгебраическим дополнением 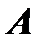некоторого элемента 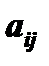соответствующий ему минор, взятый со знаком плюс или минус, смотря по тому, будет ли сумма номеров строки и столбца, которым принадлежит данный элемент, четным или нечетным числом, т.е.

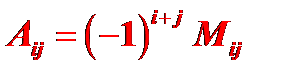
Вернемся к определителю третьего порядка:

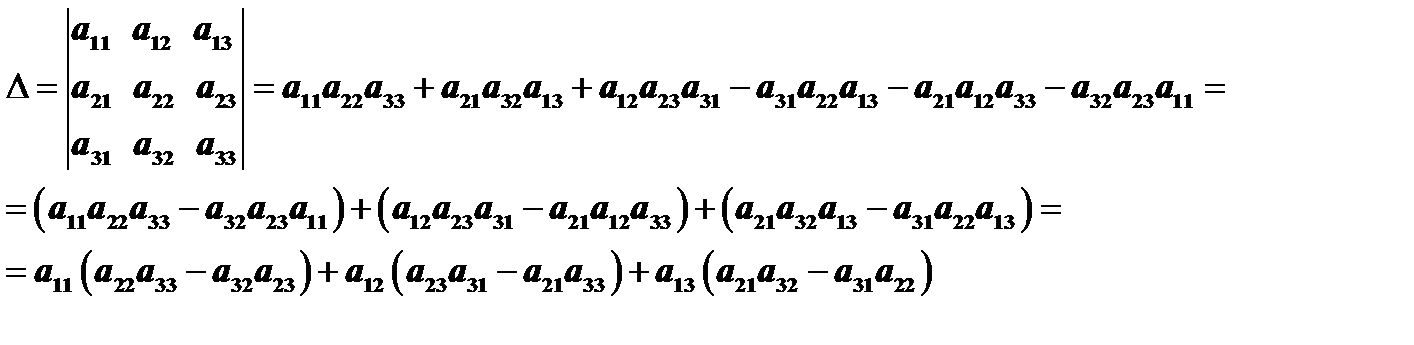
Заметим, что в скобках стоят алгебраические дополнения элементов 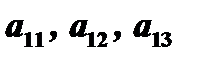, соответственно. Поэтому определитель можно переписать в виде 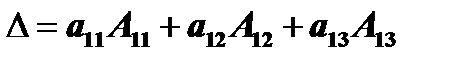. О последнем выражении говорят, что определитель разложен по элементам первой строки. Легко проверить, что аналогичная формула имеет место и по отношению к любому столбцу, а значит, и к любой строке.

Определителем 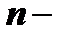го порядка, соответствующим квадратной матрице 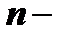го порядка, называется сумма произведений элементов какого-нибудь столбца (или строки) матрицы на их алгебраические дополнения.

Основные свойства определителей:

1. При замене строк столбцами величина определителя не меняется.

2. При перестановке двух столбцов (или строк) определитель меняет лишь знак.

3. Определитель с двумя одинаковыми столбцами (или строками) равен нулю.

4. Сумма произведений элементов некоторого ряда (столбца или строки) на алгебраические дополнения этих элементов равна определителю, а сумма произведений элементов некоторого ряда (столбца или строки) на алгебраические дополнения соответствующих элементов параллельного ряда (столбца или строки) равна нулю.

5. Множитель, общий элементам некоторого ряда (столбца или строки), можно выносить за знак определителя.

6. Определитель равен нулю, если все элементы некоторого его ряда (столбца или строки) равны нулю.

7. Если элементы некоторого ряда (столбца или строки) представляют собой сумму двух слагаемых, то определитель может быть представлен в виде суммы двух определителей, у которых элементы рассматриваемого ряда равны соответственным слагаемым.

8. Величина определителя не изменится, если к элементам некоторого ряда (столбца или строки) прибавить (или от них вычесть) элементы параллельного ряда (столбца или строки), предварительно умножив эти последние на один и тот же произвольный множитель.

Ранг матрицы

Рассмотрим матрицу типа :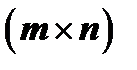

.

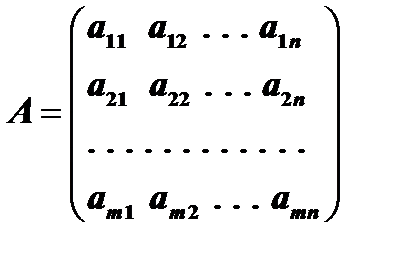Если в этой матрице выделить произвольно 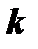столбцов и 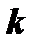строк, то элементы, стоящие на пересечении выделенных столбцов и строк, образуют квадратную матрицу 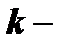го порядка. Напомним, что определитель этой матрицы 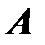обладает минорами любого порядка от 1 до наименьшего из чисел 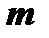и 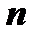. Среди всех отличных от нуля миноров матрицы 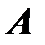найдется, по крайней мере, один минор, порядок которого будет наибольшим.

Наибольший из порядков миноров данной матрицы, отличных от нуля, называется рангом матрицы.

Если ранг матрицы равен , то это означает, что в матрице имеется, по крайней мере, один, отличный от нуля минор порядка , но всякий минор порядка, большего чем , равен нулю. Ранг матрицы обозначается через 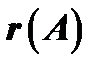или .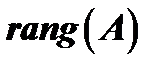

Ранг матрицы обладает следующими свойствами:

1. При транспонировании матрицы ее ранг не меняется.

2. Ранг матрицы не меняется при перестановке ее столбцов (или строк).

3. Ранг матрицы не меняется при умножении всех элементов ее столбца (или строки) на отличное от нуля число.

4. Ранг матрицы не изменится, если к одному из ее столбцов (или строк) прибавить другой столбец (соответственно строку), умножив его (ее) на некоторое число.

5. Ранг матрицы не изменится, если удалить из нее столбец, состоящий из одних нулей.

6. Ранг матрицы не изменится, если удалить из нее столбец, являющийся линейной комбинацией других столбцов.

В свойствах 5 и 6, разумеется, столбцы можно заменить строками.

Элементарными называются следующие преобразования матриц:

1) Перестановка двух любых столбцов (строк),

2) Умножение столбца (строки) на отличное от нуля число,

3) Прибавление к одному столбцу (строке) линейной комбинации других столбцов (строк).

Из свойств ранга матрицы следует, что при элементарных преобразованиях матрицы ее ранг не меняется.

Две матрицы называются эквивалентными, если одна из них получается из другой с помощью применения конечного множества элементарных преобразований. Эквивалентные матрицы не являются, вообще говоря, равными, но их ранги равны.

Канонической матрицей называется матрица, у которой в начале главной диагонали стоят подряд несколько единиц (число которых может равняться нулю), а все остальные элементы равны нулю, например

.

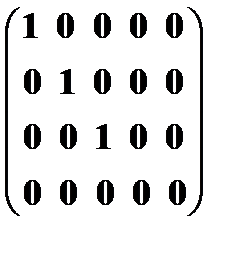При помощи элементарных преобразований строк и столбцов любую матрицу можно привести к канонической. Ранг канонической матрицы равен числу единиц на ее главной диагонали.

Замечание. На практике для вычисления ранга матрицы достаточно привести матрицу не к каноническому, а ступенчатому виду, например

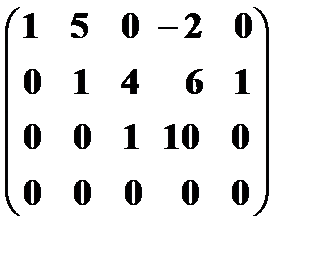
Обратная матрица

Пусть имеется невырожденная квадратная матрица 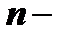го порядка

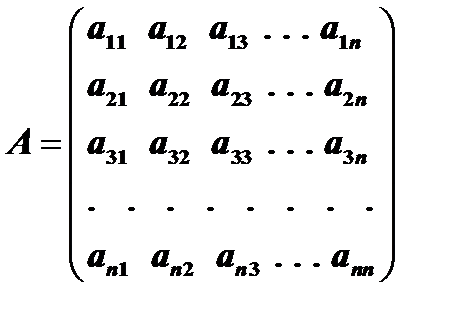, (2)

т.е. матрица, у которой определитель не равен нулю.

Обратной для данной матрицы 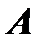вида (2) называется матрица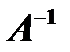 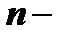го порядка, если произведение матрицы 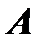на матрицу равно единичной матрице 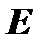, т.е. если

.

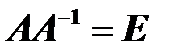Присоединенной матрицей 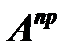к данной матрице (1) называется матрица, составленная из алгебраических дополнений элементов транспонированной матрицы .

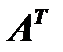Для определения обратной матрицы поступают следующим образом:

1. Пусть дана матрица (2)

2. Составим транспонированную матрицу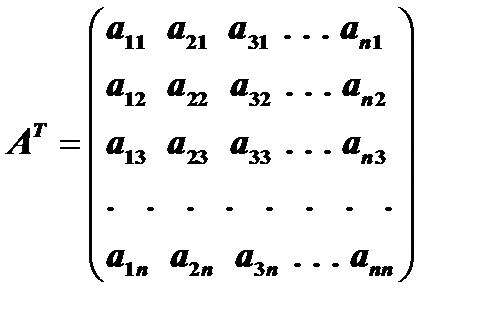

3. Составим присоединенную матрицу

4. Вычислим определитель матрицы (2)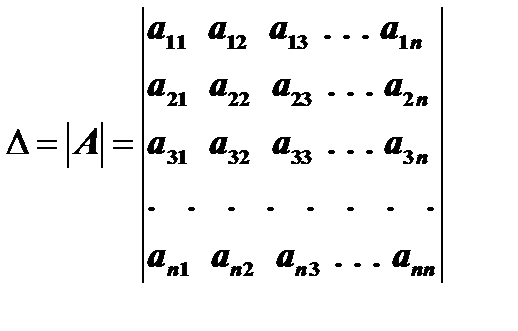

5. Обратная для данной матрицы (2) матрица 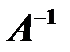получается из присоединенной к 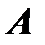матрицы 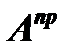путем умножения на число 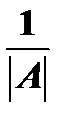, т.е. вычисляется по формуле

.

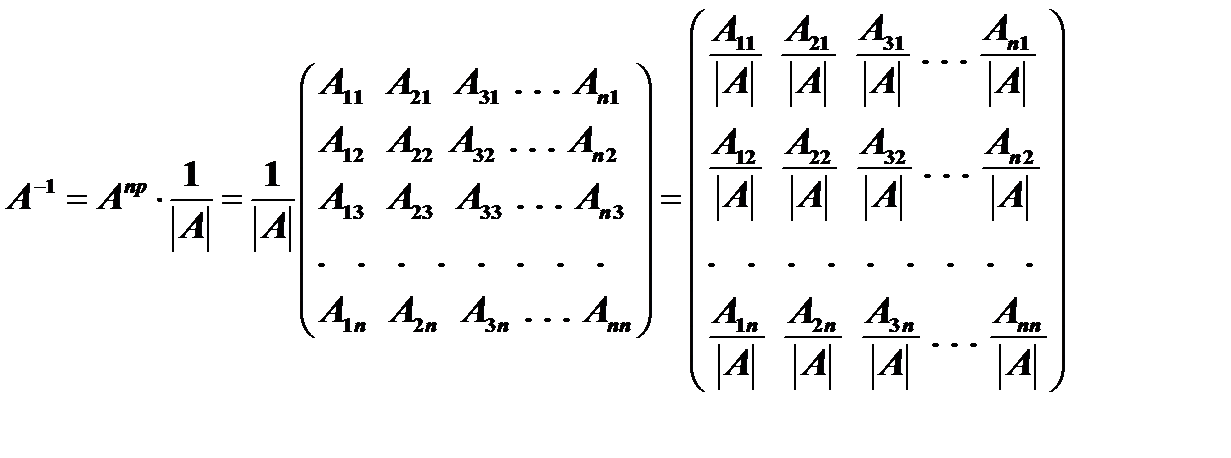Примечание. Обратную матрицу можно вычислить и с помощью элементарных преобразований. Любую квадратную матрицу 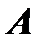путем элементарных преобразований только столбцов (или только строк) можно привести к единичной матрице 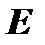. Если совершенные над матрицей 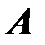элементарные преобразования в том же порядке применить к единичной матрице 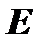, то в результате получится обратная матрица 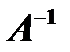. Удобно совершать элементарные преобразования над матрицам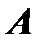и и 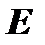одновременно, записывая обе матрицы рядом через черту. При отыскании канонического вида квадратной матрицы с целью нахождения ее ранга можно пользоваться преобразованиями строк и столбцов. В случае, когда одновременно надо найти обратную матрицу (если таковая существует), в процессе преобразований следует использовать только строки или только столбцы.

Решение системы 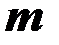линейных неоднородных уравнений

с 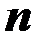неизвестными

Пусть дана система 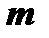линейных уравнений с 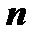неизвестными:

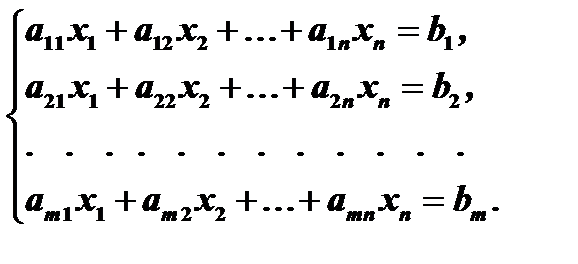
Составим матрицу из коэффициентов при неизвестных:

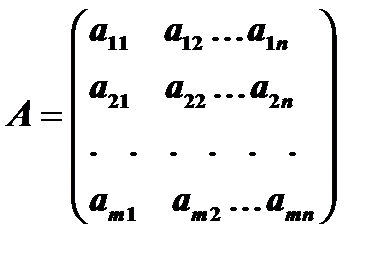
Матрица, полученная из матрицы 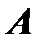путем добавления к ней справа столбца свободных членов 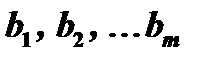, называется расширенной матрицей данной системы и обозначается символом :

.

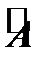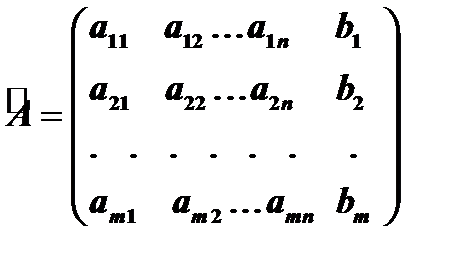Относительно данной системы имеет место следующая теорема:

Теорема Кронекера-Капелли. Система линейных уравнений совместна тогда и только тогда, когда ранг расширенной матрицы 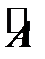равен рангу матрицы .

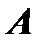Не доказывая теорему, заметим, что ранг матрицы 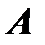, как это следует из определения расширенной матрицы, не может быть больше ранга расширенной матрицы 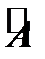. Следовательно, ранг матрицы 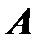меньше ранга расширенной матрицы 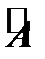или равен ему.

В теореме Кронекера-Капелли утверждается, что если ранг матрицы 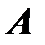равен рангу расширенной матрицы 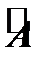, то данная система совместна, если – меньше, то система несовместна.

Если система совместна, то решение ее находят, пользуясь следующим првилом:

- если 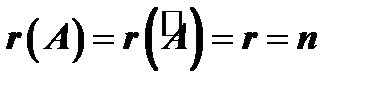, то система имеет единственное решение;

- если 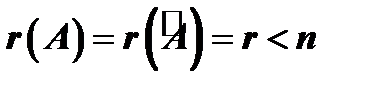, то система имеет бесчисленное множество решений.

Решение системы 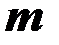линейных однородных уравнений с 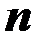неизвестными

Пусть дана система 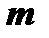линейных однородных уравнений с 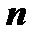неизвестными:

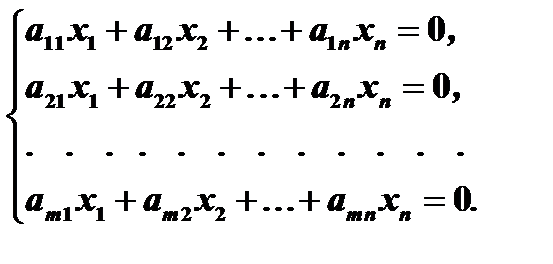
Так как последняя система получена из системы предыдущего параграфа путем замены свободных членов нулем, то для нее имеет место теорема Кронекера-Капелли. Но так как расширенная матрица для системы однородных уравнений получается из матрицы 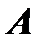системы добавлением столбца, состоящего из нулей, то ранг матрицы 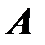этой системы всегда равен рангу расширенное матрицы 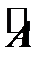, т.е. однородная система всегда совместна. При этом

- если 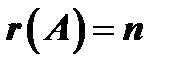, то однородная система имеет единственное нулевое решение (или, как говорят, тривиальное решение;

- если 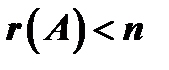, то однородная система имеет ненулевое решение.

В Е К Т О Р Ы