Неопределённый интеграл

Как известно, основной задачей дифференциального исчисления функции одной переменной является отыскание производной , или, иными словами, дифференцирование данной функции .

К вопросу отыскание производной приводит ряд задач математики и её приложений кфизики практике.

Пример 6.6.1.

Решая задачу об отыскании скорости V, которую имеем в данный момент t точка, движущаяся по закону: 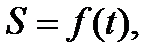мы сводим этот вопрос к отысканию производной: 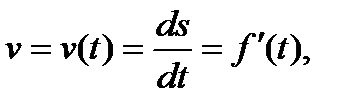так что скорость v есть производная от пути до времени.

Но часто встречается необходимость в решении задачи, обратной задаче о дифференцировании функции.

Задача состоит в следующем:

Дана функция 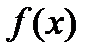, являющаяся производной некоторой функции 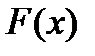; требуется найти функцию .

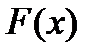(это и есть основная задача интегрального исчисления)

К такой математической задаче приводят многие физические, химические и другие задачи.

Например:

1) Задача о разыскании закона неравномерного движения материальной точки вдоль прямой по заданной скорости;

2) Задача о нахождении закона химической реакции по известной её скорости.