Исследование функций

На непрерывность

Пример6.5.1.

Найти точки разрыва функции и исследовать их характер:

а) у = 1/(х + 3); б) у =1/(1 + 2^1/х).

Построить схематично график функций в окрестности точек разрыва.

При решении примеров такого рода следует проверить выполнение условия непрерывности функции в точке

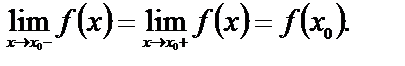
а) Функция у = 1/(х + 3) определена при всех значениях х, кроме х = -3. Так как это функция является элементарной, то она непрерывна в каждой точке своей области определения, состоящей из двух промежутков: (–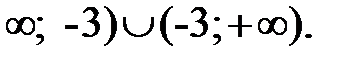

Следовательно, единственно возможной точкой разрыва является точка х = – 3. Функция определена в окрестности этой точки, в самой же точке нарушается условие непрерывности – функция в ней не определена. Для исследования характера разрыва найдем левый и правый пределы этой функции при стремлении аргумента к точке х = –3.

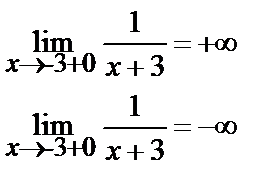
Следовательно, при х = –3 функция у = 1/(х + 3) имеет бесконечный разрыв, т.е.

y

-3

x

точка х = –3 есть точка разрыва 2 рода.

б) Рассуждая аналогично, получим, что возможной точкой разрыва функции является х = 0. Найдем односторонние пределы этой функции в точке х = 0:

y

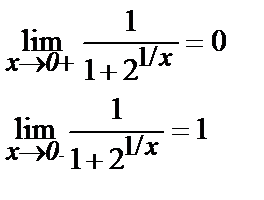
x

Таким образом, левый и правый пределы исследуемой функции при х = 0 конечны.

Поэтому х = 0 – точка скачка функции, разрыв I рода.