Первообразная функция.
Определение 1.Функция 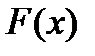 , определённая в промежутке
, определённая в промежутке 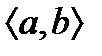 ,называется первообразной данной функции
,называется первообразной данной функции 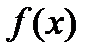 в этом промежутке , если для любого значения
в этом промежутке , если для любого значения 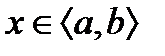 выполняется равенство:
выполняется равенство:
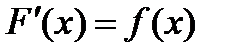 .
.
Пример 6.6.2.
1)функция 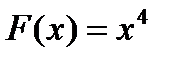 - первообразная функции
- первообразная функции
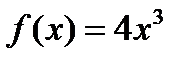 в интервале
в интервале 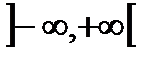 , поскольку
, поскольку 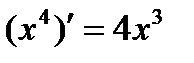 для всех Х;
для всех Х;
2)функция 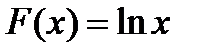 - первообразная функции
- первообразная функции 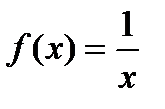 в интервале
в интервале 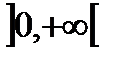 т.к.
т.к. 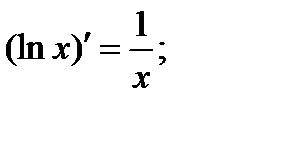
3) функция 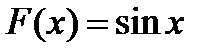 - первообразная функции
- первообразная функции 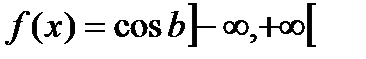 , ибо
, ибо 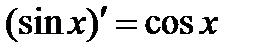 .
.
Возникает вопрос, всякая ли функция f(x) имеет на данном промежутке первообразную.
Очевидно, далеко не всякая.
В дальнейшем (в разделе “Определённый интеграл”) нами будет доказана следующая теорема:
Теорема. Любая, непрерывная на отрезке 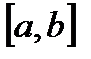 функция имеет на этом отрезке первообразную.
функция имеет на этом отрезке первообразную.
Далее возникает следующий вопрос:
Если некоторая функция имеет первообразную, то единственна ли эта первообразная?
Ответ и здесь будет отрицательным.
Так, для функциии 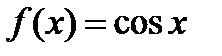 первообразной будет не только функция
первообразной будет не только функция 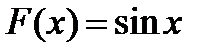 , но и
, но и
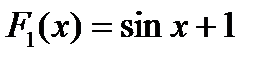 ,
, 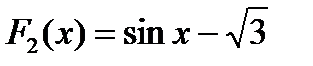 , и вообще всякая функция вида
, и вообще всякая функция вида 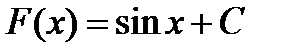 , где С – произвольная постоянная.
, где С – произвольная постоянная.
Функции такого вида исчерпывают все первообразные данной функции 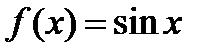 .
.
Справедлива следующая теорема, которая подтвердит последнее утверждение для любых функций.
Теорема. Если F(x) первообразная функции на 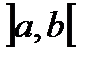 , f(х) , то
, f(х) , то 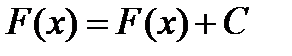 , где С производная постоянная, так же является её первообразной.
, где С производная постоянная, так же является её первообразной.
Определение 2. неопределённым интегралом от данной функции 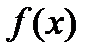 называется множество всех её первообразных:
называется множество всех её первообразных: 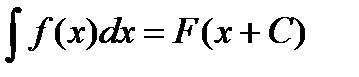 , где
, где 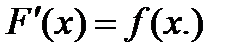
Знак 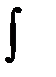 - называется знаком неопределённого интеграла; функция
- называется знаком неопределённого интеграла; функция 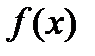 - подынтегральной функцией; выражение
- подынтегральной функцией; выражение 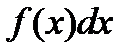 - подынтегральным выражением;
- подынтегральным выражением;  - переменное интегрирование.
- переменное интегрирование.
Операция нахождения первообразной данной функции называется интегрирование.
Таким образом, чтобы найти неопределенный интеграл от данной функции 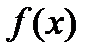 , достаточно найти какую - либо её первообразную
, достаточно найти какую - либо её первообразную 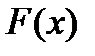 и составить сумму
и составить сумму 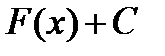 ,где С – производная постоянная.
,где С – производная постоянная.
Пример6.6.3. 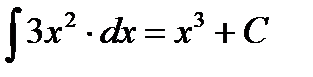 ;
; 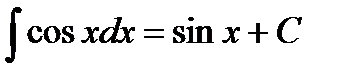 .
.
Дата добавления: 2016-06-05; просмотров: 2371;











