Уравнение гармонического баланса.

Составим уравнение по структурной схеме системы управления в канонической форме рис. 1, используя комплексное обозначение для гармонического сигнала ( 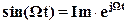) и очевидное соотношение x =- y. То получаем соотношение:

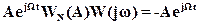(30)

Сокращаем на неравный нулю множитель и получаем:

(31)

Это уравнение называется уравнением гармонического баланса.

Если удастся найти два действительных числа А=А₀ и ω=Ω, которые обращают уравнение (31) в тождество, то ,согласно вышеприведенным рассуждениям, в системе имеют место автоколебания почти гармонической формы с частотой Ω и амплитудой А.

Подчеркнем, что мы имеем дело не с математическим доказательством, а только с правдоподобными рассуждениями!

Если в исходной системе нелинейный элемент заменить гармоническим коэффициентом усиления 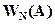, то нелинейная система превратится в некоторую линеаризованную систему, содержащую вместо нелинейного блока пропорциональное звено. Иными словами 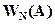можно рассматривать как некоторый коэффициент усиления, вообще говоря, комплексный.

Эта линеаризованная система по условию находится на границе устойчивости, т.к. в ней циркулирует гармоническое колебание. Этот факт и отражается уравнением гармонического баланса, которое можно рассматривать как уравнение границы устойчивости линейной системы с коэффициентом усиления .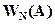

Уравнение (31) удобно решать графически, предварительно преобразовав его в соотношение:

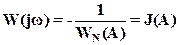(32)

Или в соотношение:

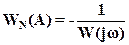(33)

На комплексной плоскости строятся два графика, один из которых оцифровывается по амплитуде, а другой по частоте. В точке пересечения этих графиков, если она имеет место, по оцифровке кривых определяем значение А и Ω.

Реально могут иметь место автоколебания, только если они устойчивые. В качестве критерия устойчивости, разумеется, весьма приближённого, воспользуемся следующим рассуждением, которое является обобщением критерия Найквиста, на случай, когда коэффициент усиления комплексный. Точку -1 у нас заменит точка 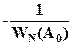( согласно принятым обозначениям J(A₀) ). Точка J(A₀) находится на кривой W(jω), т.е. гармоническая линеаризованная система находится на границе устойчивости. Предположим, что амплитуда увеличилась от А₀ к А₁. Если точка J(A₁) будет находится вне кривой W(jω), значит линеаризованная система устойчива и колебания затухают. Если точка J(A₁) переместится внутрь кривой, т.е. будет охватываться W(jω), то, следовательно, система станет неустойчивой и амплитуда А будет ещё больше возрастать. Таким образом, мы можем сформулировать следующий приближённый критерий: если при увеличении амплитуды точка J(A) сдвигается вне кривой W(jω), то автоколебания устойчивы. В том случае, когда с увеличением амплитуды точка J(A) сдвигается внутрь кривой W(jω), то колебания неустойчивые.

Некоторые свойства уравнения гармонического баланса.

Запишем 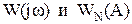в показательной форме.

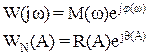(34)

Согласно (34) уравнение гармонического баланса можно переписать в форме системы уравнений (уравнения для модулей и уравнения для фаз).

Уравнение модулей:

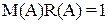
Уравнение фаз: (35)

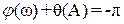
Из уравнения гармонического баланса, записанного в виде (35), следует важный вывод.

Если нелинейный элемент в системе однозначный, то частота автоколебаний совершенно не зависит от его формы и целиком определяется линейной частью.

Указанное свойство следует из того, что для однозначной функции N(x) гармонический коэффициент усиления действителен (q’(A) = 0, θ(A) = 0).