Передаточная функция W(p) выбрана таким образом, что линейная система на рисунке 1 обладает свойством условной устойчивости по Бодэ.
Коротко говоря, эти системы можно охарактеризовать следующим свойством:
существует такое значение К=К1, что система устойчива при К>К1 и неустойчива при К<К1, т.е. интервалу устойчивости предшествуетинтервал неустойчивости.
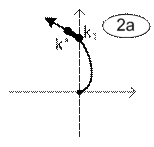
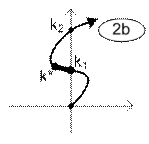
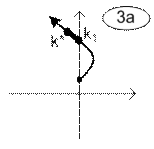
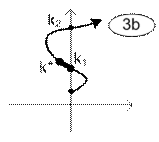
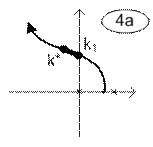
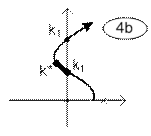
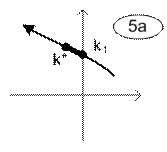
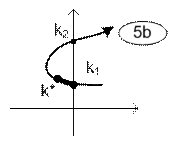
Возможны различные варианты расположения интервалов устойчивости и неустойчивости замкнутой линейной системы, условно показанные расположением траектории одного из корней характеристического уравнения в таблице 2.
В таблице 1 приведены аналитические выражения некоторых передаточных функций W(p) разомкнутых систем для условно устойчивых по Боде замкнутых систем.
Таблица 1 (передаточных функций разомкнутых систем для условно устойчивых по Боде замкнутых систем).
Передаточные функции W(p).
 1a 1a
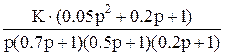
|  1b 1b
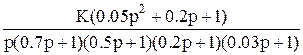
|
 2а 2а
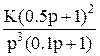
|  2b 2b
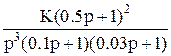
|
 3а 3а
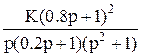
|  3b 3b
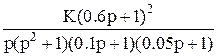
|
 4а 4а
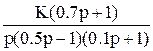
|  4b 4b
 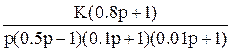
|
 5а 5а
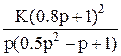
| 5b
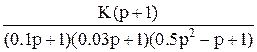
|
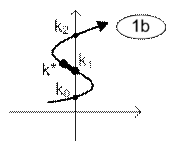
Таблица 2.
Варианты траекторий корней условно устойчивых систем.
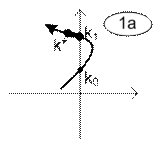
| 
|
| 
|
| 
|
| 
|
| 
|
Выбираем значение К из условий устойчивости замкнутой системы (рис. 2). Это значение должно находится внутри интервалаустойчивости:
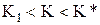
Где величина К* зависит от ряда конкретных причин, на которых не будем останавливаться, но существенно, что она близка к границе устойчивости.
Почему решили выбирать К именно таким образом, чтобы обнаружить влияние ограничения сигнала на динамику системы? Дело в том, что в ряде математических работ уже давно указывалось на то, что участок слева от границы устойчивости наиболее опасный.
Пример 1.
Рассмотрим случай, показанный в таблице 2 на рисунке 1а.
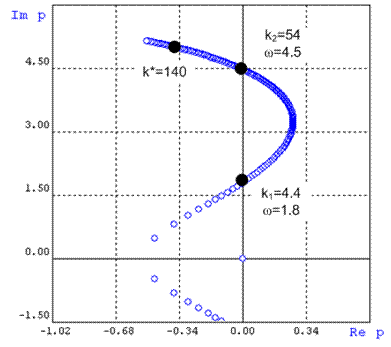
Рис. 4
Значимая часть корневого годографа.
На вход системы (рис.1) подается импульс, показанный на рисунке 3, высота которого h=10, а ширина T=1. При К 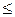 140 на выходе системы получаем автоколебания, к примеру, на рис.5 показаны автоколебания при К=139:
140 на выходе системы получаем автоколебания, к примеру, на рис.5 показаны автоколебания при К=139:
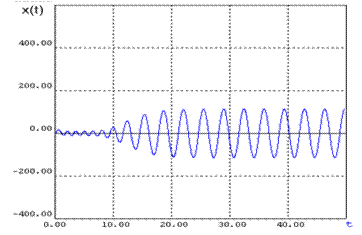
Рис. 5 Процесс регулирования.
При дальнейшем увеличении коэффициента усиления автоколебания исчезают. Например, при К > 140 на выходе системы получаем сходящийся процесс (рис. 6):
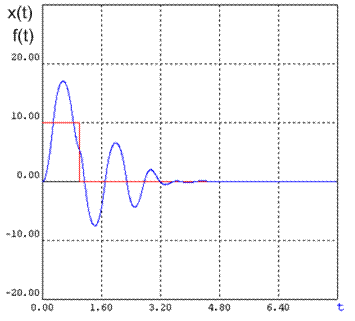
Рис. 6
Процесс регулирования.
Пример 2.
Рассмотрим случай, показанный в таблице 2 на рисунке 3b.
В этом примере рассмотрим самое опасное явление, к которому может приводить простейший нелинейный элемент насыщения – возникновение практически расходящихся колебаний.
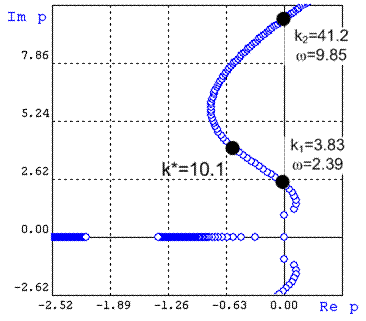
Рис. 7
Значимая часть корневого годографа.
Положим К=4 и подадим на вход замкнутой системы импульс, показанный на рисунке 3, высота которого h=6, а ширина T=1. Как видно на рис. 8, в системе имеет место расходящийся процесс:
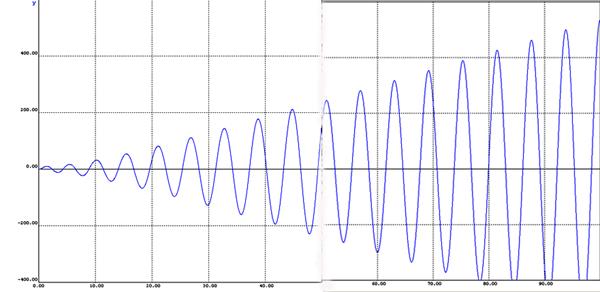
Рис. 8
Процесс регулирования.
При дальнейшем увеличении величины К, мы получим сходящийся процесс. На рисунке 9 показан сходящийся процесс при К=10,2.
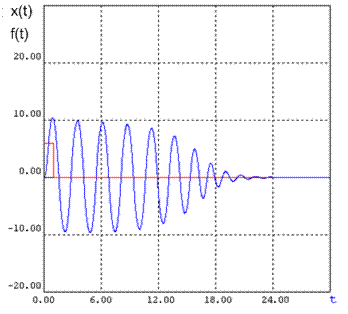
Рис. 9
Процесс регулирования.
Вывод.
На основе проведенного численного эксперимента можно сделать заключение, что даже такой простой нелинейный элемент, как ограничение модуля сигнала, может приводить к возникновению весьма опасных динамических процессов: возникновение автоколебаний с большой амплитудой или, что самое опасное, возникновение практически расходящегося процесса. Эти факты указывают на то, что ни в коем случае при составлении математической модели систем автоматического управления не следует бездумно пренебрегать нелинейными явлениями.
В заключение, рекомендуем читателю ознакомиться с книгой Б. Хэссарда, Н. Казаринова и И. Вэна, «Теория и приложения бифуркации рождения цикла», Москва «Мир» 1985, стр. 102, пример «Центробежный регулятор».
Дата добавления: 2017-01-16; просмотров: 1720;











