Гармонический коэффициент линеаризации нелинейного элемента.

Предположим, что на вход нелинейного элемента поступает гармонический сигнал.

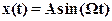(7)

Разлагаем сигнал u(t) в ряд Фурье, и отбрасываем все слагаемые, содержащие аргументом Ωk, где k>1, т.е. все гармоники выше первой.

Записываем коэффициенты первой гармоники разложения в ряд Фурье:

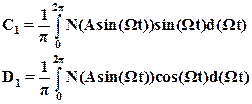(8)

Учитывая (7) и (8), сигнал на выходе нелинейного элемента можно записать

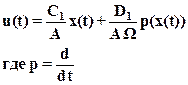(9)

Обозначим

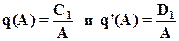(10)

«Штрих» в обозначении q(A) – не знак производной. (Просьба не путать!)

Функции q(A) и q’(A) называют гармоническими коэффициентами усиленияN(x).

Функцию

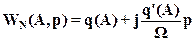(11)

называют гармонически линеаризованной передаточной функцией нелинейного элемента

Функцию

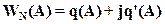(12)

называют амплитудно-фазовой характеристикой.

Выше мы использовали обозначения и терминологию Е.П.Попова, распространенную в учебной литературе по теории управления.

Отметим, что на наш взгляд гармоническим коэффициентом усиления N(x) целесообразно было бы назвать функцию .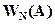

В основополагающей работе [x] Гольдфарб использовал терминологию из теории переменных токов: адмитанц (комплексное сопротивление) и импеданц (комплексная проводимость).

Согласно методу «мнимых амплитуд» в теории переменных токов входной сигнал можно записать в форме:

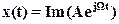(13)

А выходной сигнал соответственно:

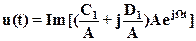(14)

Соотношении между входом и выходом, равное

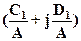(15)

Гольдфарб называл адмитанцем нелинейного элемента, обратную ему величину – импеданцем. Очевидно, что адмитанц равен .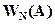

Впоследствии Л.С.Гольдфарб стал использовать для 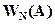название комплексный коэффициент усиления нелинейного элемента.

В данной работе мы условимся называть 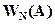гармоническим коэффициентом усиления. Условимся использовать обозначение:

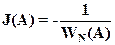(16)