Численный эксперимент. Опасные явления в нелинейных системах.

1. Методы исследования динамики линейных систем автоматического управления с постоянными коэффициентами разработаны исключительно полно. Для нелинейных систем положение несравненно хуже. Даже в простейшем случае, когда нелинейная система состоит из одного нелинейного статического и одного линейного блоков, могут возникать очень сложные проблемы. Поэтому мы проиллюстрируем эти явления численным экспериментом на ПК с помощью программ пакета TAY3 (в ряде случаев расчет дублировался на MathCAD11).

Цель данного приложения показать, к каким опасным динамическим процессам может привести столь не сложный нелинейный эффект, как ограничение величины сигнала в линии передачи системы.

Пусть структурная схема имеет вид, показанный на рисунке 1:

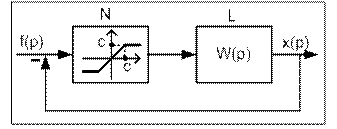
Рис. 1

Выясним путем численного эксперимента, что в структурной схеме на рисунке 1, состоящей из НЭ «насыщение» и линейного блока с передаточной функцией W(p), возможны, при определенных условиях, возникновение автоколебаний и, что гораздо хуже, возникновение практически расходящихся процессов. (Мы не имеем возможности утверждать, что возникает расходящийся процесс, и пишем только о практическирасходящемся процессе, так как речь идет о численном эксперименте).

2. Эксперимент проводится следующим образом.

Выбираем определенным способомвеличину коэффициента усиления линейного блока К. Величину К выбираем такой, чтобы линейная система, получаемая из исходной нелинейной (рис. 1), когда нет ограничения в блоке N (рис. 2), была устойчивой.

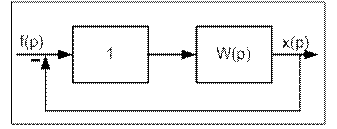
Рис. 2

Подаем на вход нелинейной системы (рис. 1) прямоугольный импульс, показанный на рисунке 3, и наблюдаем поведение сигнала х(t) на выходе системы.

Рис. 3

3. Перейдем к вопросу о выборе коэффициента усиления К в линейной системе, показанной на рисунке 1.