Некоторые важные свойства гармонического коэффициента усиления.
1) Если нелинейная функция N(x) однозначна, то коэффициент D1=0. Коэффициент D1 ≠0 только если N(x) имеет петлю гистерезиса. Дело в том, что D1 , как будет показано ниже, равен площади этой петли гистерезиса, умноженной на константу. Докажем этот факт.
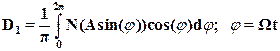 (17)
(17)
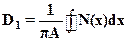 (18)
(18)
Пусть график N(x) имеет вид:
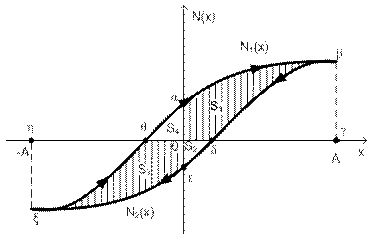 Рис. 6
Рис. 6
|
Площадь петли 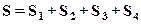
При возрастании х ( 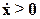 ) N(x)=N1(x), т.е. движение осуществляется по линии ξθαβ.
) N(x)=N1(x), т.е. движение осуществляется по линии ξθαβ.
При убывании х ( 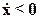 ) N(x)=N2(x), т.е. движение осуществляется по линии βδεξ.
) N(x)=N2(x), т.е. движение осуществляется по линии βδεξ.
Переменная х изменяется в интервале (-А;А).
Площадь петли
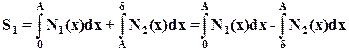 (19)
(19)
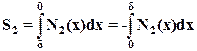 (20)
(20)
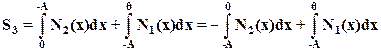 (21)
(21)
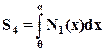 (22)
(22)
Переменная х изменяется по синусоидальному закону, как показано на рисунке
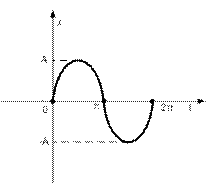 Рис. 7
Рис. 7
|
Вычисление интеграла от нуля до двух пи для вычисления коэффициента можно записать
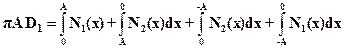 (23)
(23)
Учитывая, что (23)
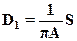 (24)
(24)
Таким образом, если функция N(x) однозначна, и , следовательно, площадь петли величина S равна нулю, то коэффициент D1 также равен нулю.
2) Если функция N(x) однозначна, то ее гармонический коэффициент усиления является действительнозначной функцией амплитуды (q(A)).
Если функция N(x) однозначна и симметрична относительно начала координат, то разложение Фурье содержит только нечетные значения k (1,3,5…).
Дата добавления: 2017-01-16; просмотров: 1737;











