Метод гармонического баланса для исследования автоколебаний, имеющих форму, близкую к синусоиде.

В сороковых годах Л.С.Гольдфарбом был предложен удивительно простой метод [x] определения автоколебаний в системах автоматического управления. Метод не является математически доказанным утверждением и базируется на правдоподобных рассуждениях. Этот метод позднее был с исключительной полнотой развит в работах Е.П.Попова [x]. Сразу же отметим очень важное обстоятельство. Метод не дает информации о жестком или мягком режиме возникновения автоколебаний.

Перейдём к его описанию. Л.С.Гольдфарб обратил внимание, что очень часто автоколебания в технических системах авторегулирования на выходе объекта имеют почти гармонический характер. Запись колебаний выходной координаты y(t) может быть аппроксимировано функцией Asin(Ωt), если соответственно подобрать числа А и Ω. На основе этого наблюдения Л.С.Гольдфарб построил логику своих рассуждений на следующем исходном предположении.

Сигнал на входе нелинейного элемента (x(t)=-y(t)) следует принять равным

x(t)=Asin(Ωt) (2)

где числа А и Ω необходимо вычислить.

Из исходного предположения вытекает, что автоколебания в системе имеют период:

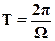(3)

Сигнал на выходе нелинейного элемента u(t)=N(Asin(Ωt)) является периодической функцией с периодом Т, но форма его колебаний может быть очень далека от гармонической, например, прямоугольная волна и т.д. сигнал u(t) представляет собой ряд Фурье:

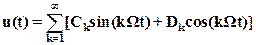(4)

(Для простоты предположим, что постоянная составляющая отсутствует, т.е. D₀=0.)

Далее по логике рассуждений необходимо, чтобы линейный блок пропускал только первую гармонику сигнала u(t), т.е. АЧХ W(p) имело форму фильтра высоких частот.

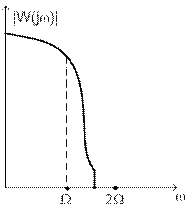Рис. 3

Физически такая АЧХ невозможна у линейного блока, однако допустима ситуация, когда АЧХ имеет форму, показанную на рисунке 4. В этом случае говорят, что линейный блок удовлетворяет «гипотезе фильтра».

Возможна ситуация, когда АЧХ линейного блока удовлетворяет гипотезе резонанса и имеет вид, показанный на рисунке 5, но этот случай часто встречается в теории колебаний и нехарактерен для задач авторегулирования. Далее будем предполагать, что АЧХ удовлетворяет гипотезе фильтра.

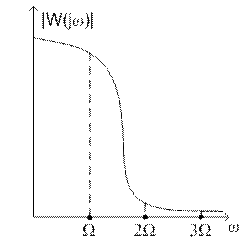Рис. 4а

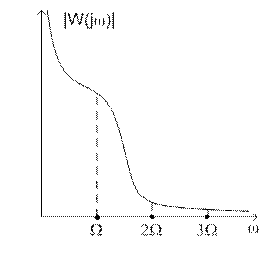Рис. 4b

На рисунке 4а приведена амплитудно-частотная характеристика в случае, когда W(p) не содержит интегрирующее звено, на рисунке 4b – когда содержит.

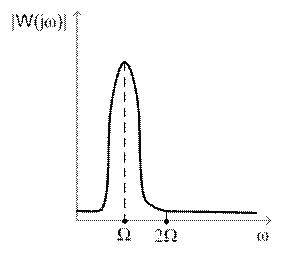Рис. 5

Автоколебания – это стационарный процесс, поэтому при его рассмотрении мы предполагаем, что он длится уже достаточно долго, и переходный процесс линейного блока давно затух. Следовательно, на выходе линейного блока мы можем рассматривать только установившийся процесс, который будет равен

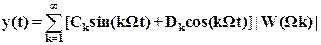(5)

Предполагаем, что для k > 1 величина |W(Ωk)| пренебрежимо мала, что соответствует «гипотезе фильтра».

Если удовлетворяется «гипотеза фильтра», то приближённо можно записать

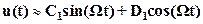(6)

Отметим, что идеальный случай, когда |W(Ωk)|=0 при k>1, принципиально невозможен.

Подчеркнем, что в формуле (6) мы отбросили высшие гармоники не потому, что они малы, а потому, что их влияние на выходной сигнал системы пренебрежимо мало благодаря «гипотезе фильтра».

Таким образом, задача состоит в том, чтобы зная N(x) и W(p), вычислить числа А и Ω. Для решения этой задачи предварительно введем два важных понятия.