Производная функции, заданной неявно
Неявная функция-это функции f(x,y)=0, в которой переменные x и y расположены «вперемешку». Например, 4 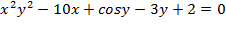 . Причем никакими способами невозможно выразить «игрек» только через «икс».
. Причем никакими способами невозможно выразить «игрек» только через «икс».
Находить производную от функции, заданной неявно, в общем то, не так сложно! Все правила дифференцирования, таблица производных элементарных функций остаются в силе. Разница в одном своеобразном моменте, переменная у воспринимается как сложная функция.
Пример 1. Продифференцируем обе части выражение 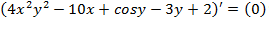 .
.
Решение.
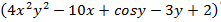 =4
=4  2
2 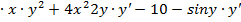 =
=
8x 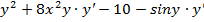 =0
=0
Теперь сгруппируем элементы равенства и выразим выражение явно относительно производной y’:
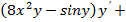 8x
8x 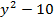 =0 или
=0 или 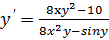
Таким образом, если предствить функцию в виде F(x.y)=0, то можно записать формулу производной в виде:
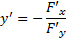
Пример 2.
Найти производную от функции, заданной неявно 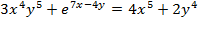
Навешиваем штрихи на обе части:
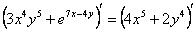
Используем правила линейности:
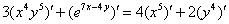
Находим производные:
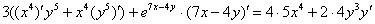
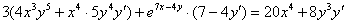
Раскрываем все скобки:
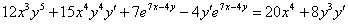
Переносим все слагаемые с 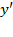 в левую часть, остальные – в правую часть:
в левую часть, остальные – в правую часть:
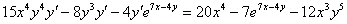
В левой части выносим 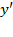 за скобку:
за скобку:
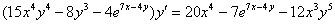
Окончательный ответ:
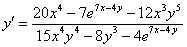
Правило Лопиталя для нахождения предела функции.
1. Теорема. Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных (конечному или бесконечному), если последний существует в указанном смысле.
т.е. при раскрытии неопределенностей вида 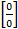 или
или  можно использовать формулу:
можно использовать формулу:
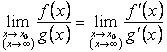 .
.
Пример.
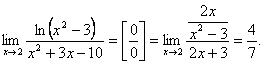
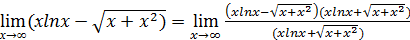 =
= 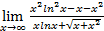 =
= 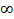
Пример: Найти предел 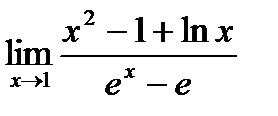 .
.
Как видно, при попытке непосредственного вычисления предела получается неопределенность вида 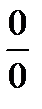 . Функции, входящие в числитель и знаменатель дроби удовлетворяют требованиям теоремы Лопиталя.
. Функции, входящие в числитель и знаменатель дроби удовлетворяют требованиям теоремы Лопиталя.
f¢(x) = 2x + 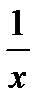 ; g¢(x) = ex;
; g¢(x) = ex;
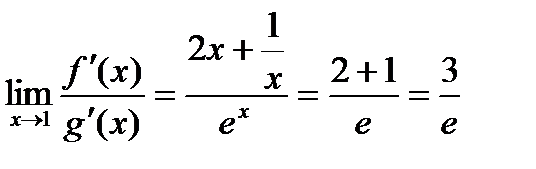 ;
;
Пример: Найти предел 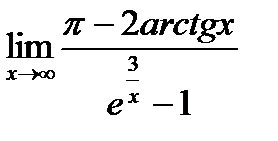 .
.
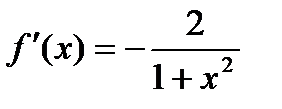 ;
; 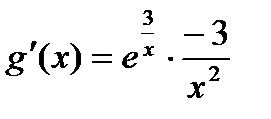 ;
;
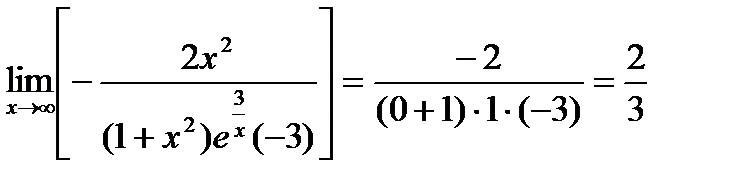 .
.
Если при решении примера после применения правила Лопиталя попытка вычислить предел опять приводит к неопределенности, то правило Лопиталя может быть применено второй раз, третий и т.д. пока не будет получен результат. Естественно, это возможно только в том случае, если вновь полученные функции в свою очередь удовлетворяют требованиям теоремы Лопиталя.
Пример: Найти предел 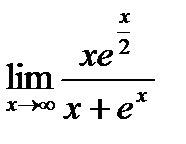 .
.
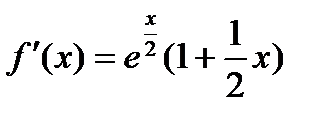 ;
; 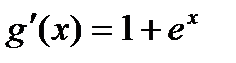 ;
;
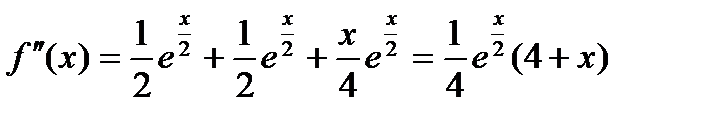 ;
; 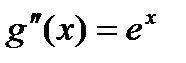 ;
;
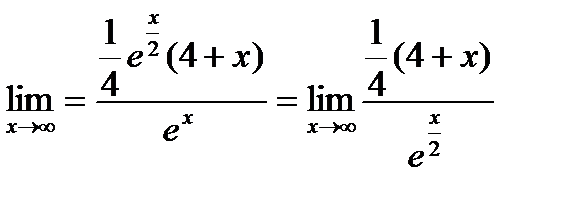
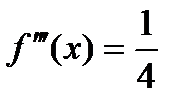 ;
; 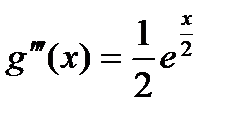 ;
; 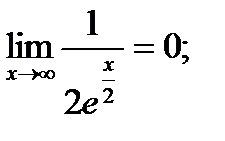
Следует отметить, что правило Лопиталя – всего лишь один из способов вычисления пределов. Часто в конкретном примере наряду с правилом Лопиталя может быть использован и какой – либо другой метод (замена переменных, домножение и др.).
Пример: Найти предел 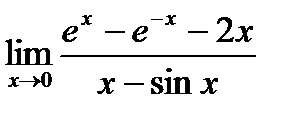 .
.
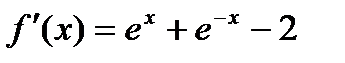 ;
; 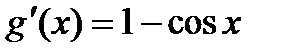 ;
;
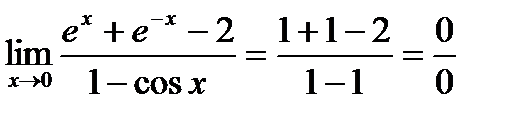 - опять получилась неопределенность. Применим правило Лопиталя еще раз.
- опять получилась неопределенность. Применим правило Лопиталя еще раз.
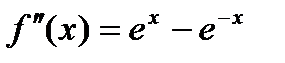 ;
; 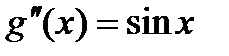 ;
;
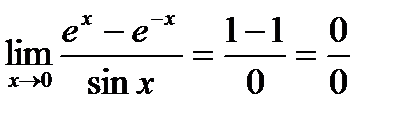 - применяем правило Лопиталя еще раз.
- применяем правило Лопиталя еще раз.
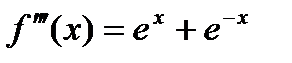 ;
; 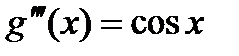 ;
;
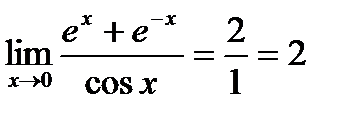 ;
;
Неопределенности вида 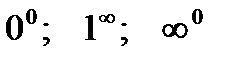 можно раскрыть с помощью логарифмирования. Такие неопределенности встречаются при нахождении пределов функций вида
можно раскрыть с помощью логарифмирования. Такие неопределенности встречаются при нахождении пределов функций вида 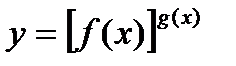 , f(x)>0 вблизи точки а при х®а. Для нахождения предела такой функции достаточно найти предел функции lny = g(x)lnf(x).
, f(x)>0 вблизи точки а при х®а. Для нахождения предела такой функции достаточно найти предел функции lny = g(x)lnf(x).
Пример: Найти предел 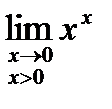 .
.
Здесь y = xx, lny = xlnx.
Тогда 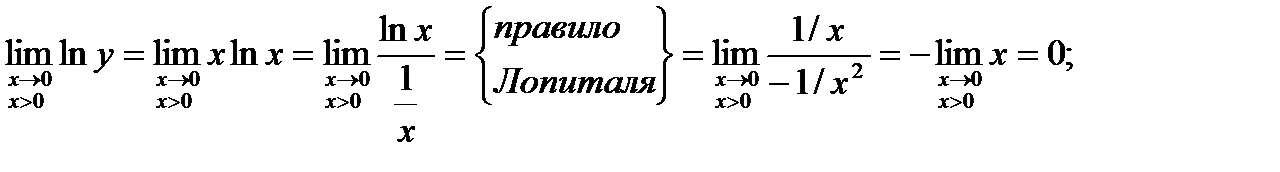 .
.
Следовательно 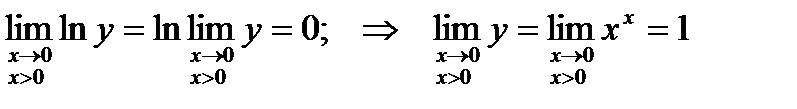
Пример: Найти предел 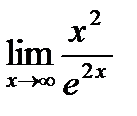 .
.
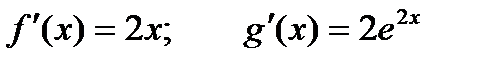 ;
; 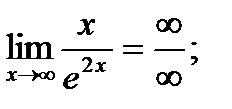 - получили неопределенность. Применяем правило Лопиталя еще раз.
- получили неопределенность. Применяем правило Лопиталя еще раз.
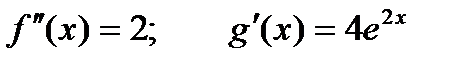 ;
; 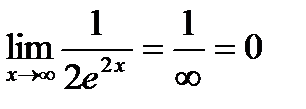 ;
;
Дата добавления: 2016-06-05; просмотров: 2134;











