Производная сложной функции.
На практике с производной сложной функции приходится сталкиваться очень часто. Правило дифференцирования сложной функции в общем виде таково: 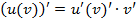 . Можно так сказать: «производная сложной функции равна произведению производных»
. Можно так сказать: «производная сложной функции равна произведению производных»
Здесь у нас две функции – u и v, причем функция v, образно говоря, вложена в функцию u. Функция такого вида (когда одна функция вложена в другую) и называется сложной функцией. Например, y=lnsinx.
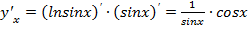 Здесь в логарифм вложена функция синус. Поэтом в начале берём производную от логарифма, а затем производную от аргумента, т.е. от синуса.
Здесь в логарифм вложена функция синус. Поэтом в начале берём производную от логарифма, а затем производную от аргумента, т.е. от синуса.
Пример двойного вложения. 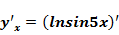 =
= 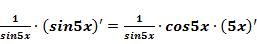 =
= 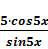
Другие примеры
Найти производную функции:
1.у= 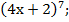
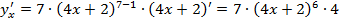 =28
=28 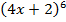
Здесь главной является степенная функция. Соответственно производня берются по правилам степенной функции: 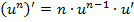
2.Найти производную. 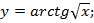 Здесь в символах u(v) главной является функция arctg, а аргументом является
Здесь в символах u(v) главной является функция arctg, а аргументом является 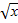 , поэтому по таблице производных распишем:
, поэтому по таблице производных распишем:
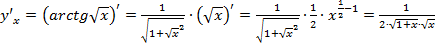
3. Найти производную y= 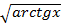 ; Здесь главной функцией является степенная зависимость, которую лучше представить в виде y=
; Здесь главной функцией является степенная зависимость, которую лучше представить в виде y= 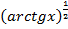 и далее применить формулу
и далее применить формулу 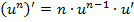
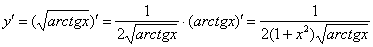
4. Сравните результаты производных двух функций: y= 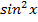 и y=sin
и y=sin 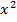 .
.
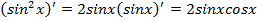 и
и
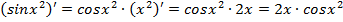
5. Найти производную функции y=y= 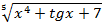
Здесь имеется корень, а для того, чтобы продифференцировать корень, его нужно представить в виде степени 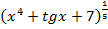 . Таким образом, сначала приводим функцию в надлежащий для дифференцирования вид:
. Таким образом, сначала приводим функцию в надлежащий для дифференцирования вид:
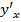 =
= 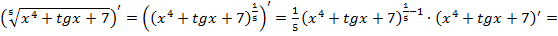
= 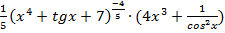 =
= 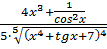 .
.
6. Найти производную функции 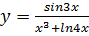
Здесь можно использовать правило дифференцирования частного 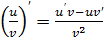
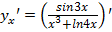 =
= 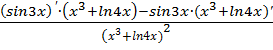 =
=
= 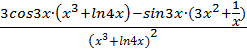 .
.
7. Найти производную функции y= 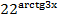 . Число 22 являтся основанием показательной функции.
. Число 22 являтся основанием показательной функции.
Это есть показательная функция, которая дифференцируется по правилу:
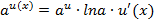 , т.е. эта функция вначале повторяется. затем умножается на натуральный логарифм от основания и далее берётся производная от степени. Твким образом, имеем:
, т.е. эта функция вначале повторяется. затем умножается на натуральный логарифм от основания и далее берётся производная от степени. Твким образом, имеем:
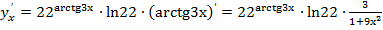 =
= 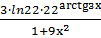
8.Найти производную y= 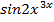
Когда в показательной функции основанием является не число, а функция, такая функция называется сложно показательной функцией. Вычисление производной при этом производится через логарифмирование функции по формуле:
y= 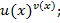 lny=ln
lny=ln 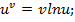
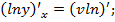
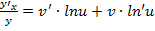 ;
;
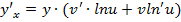 . Таким, образом можем для данной функции записать:
. Таким, образом можем для данной функции записать:
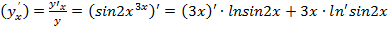 = 3lnsin2x+3x
= 3lnsin2x+3x 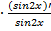
Или окончательно: 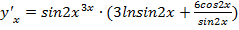
Производная функции, заданная параметрически
Пусть задана функция y=f(x) через параметр t:
x=x(t) и y=y(t). Необходимо определить производную 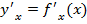 . Выразим эту производную через отношения дифференциалов:
. Выразим эту производную через отношения дифференциалов:
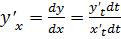 =
= 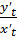 - это есть производная первого порядка.
- это есть производная первого порядка.
Определим теперь производную второго порядка. Для этого представим вычисление второй производной как повторная производная от первой производной:
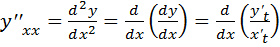 =
= 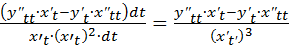
Пример.
1. Найти первую и вторую производные от функции.
x = 3 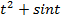
y = cos2t
Решение . 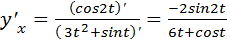
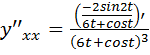 =
= 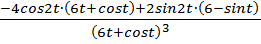
Задание для самостоятельной работы
Найти производную функций: Ответы:
1. y= 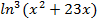 1.
1. 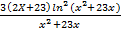
2. y= 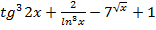 2.6
2.6 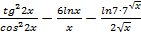
3. y= 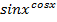
4. y=ctg2x 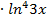
5.y= 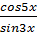
.
Дата добавления: 2016-06-05; просмотров: 2647;











