Вычисление площади криволинейной трапеции заданной в параметрической форме
Вычисление площадей плоских фигур
Если функция 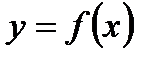 , определена и интегрируема на отрезке
, определена и интегрируема на отрезке 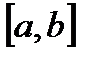 , причем
, причем 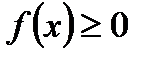 на этом отрезке, то площадь криволинейной трапеции определяется определенным интегралом.
на этом отрезке, то площадь криволинейной трапеции определяется определенным интегралом. 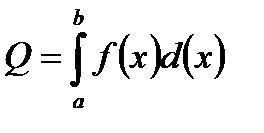 . Если функция
. Если функция 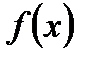 отрицательна на отрезке
отрицательна на отрезке
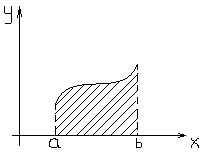
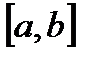 , то
, то 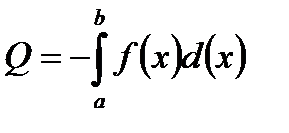 . Если функция принимает как положительные, так и отрицательные значения, то для определения площади криволинейной трапеции в обычном смысле, необходимо разбить отрезок
. Если функция принимает как положительные, так и отрицательные значения, то для определения площади криволинейной трапеции в обычном смысле, необходимо разбить отрезок 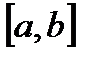 , на части, соответствующие участкам знакопостоянства функции
, на части, соответствующие участкам знакопостоянства функции 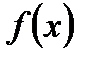 . Площадь криволинейной трапеции будет выражена:
. Площадь криволинейной трапеции будет выражена: 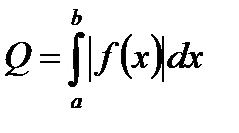 . Если требуется вычислить площадь области ограниченной двумя кривыми
. Если требуется вычислить площадь области ограниченной двумя кривыми 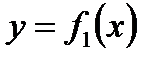 и
и 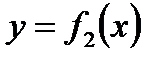 на отрезке
на отрезке 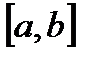 . Причем
. Причем 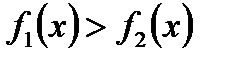 , то достаточно представить искомую площадь в виде разности площадей двух криволинейных трапеций.
, то достаточно представить искомую площадь в виде разности площадей двух криволинейных трапеций.
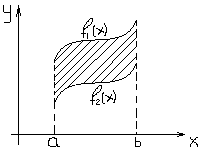
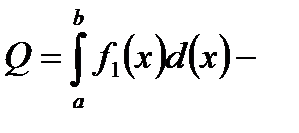
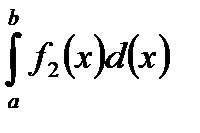
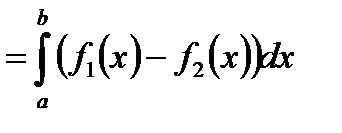
В случае более сложных областей, искомую площадь разбивают на части и каждую часть рассчитывают по отдельности.
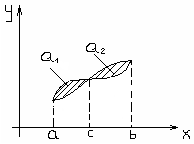
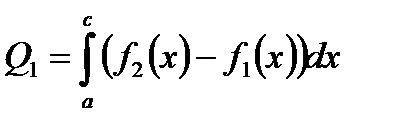
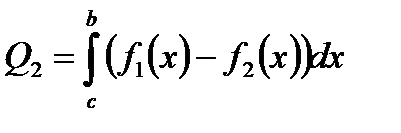
Вычисление площади криволинейной трапеции заданной в параметрической форме
Пусть функция y=f(x) на отрезке [a,b] задана параметрически
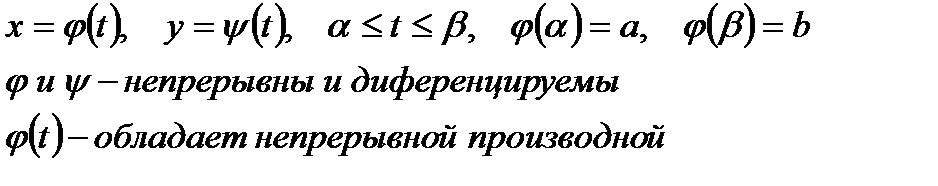
Следовательно, площадь криволинейной трапеции может быть вычислена по формуле
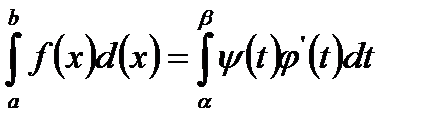
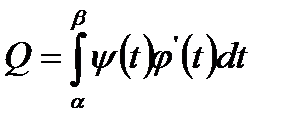
Пример. Вычислить площадь эллипса. 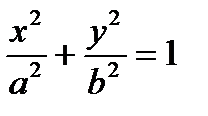
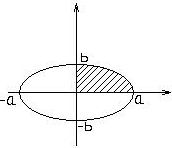 Эллипс- фигура симметричная по всем осям, для вычисления площади эллипса достаточно вычислить площадь заштрихованной части. Используя тригонометрическую параметризацию
Эллипс- фигура симметричная по всем осям, для вычисления площади эллипса достаточно вычислить площадь заштрихованной части. Используя тригонометрическую параметризацию 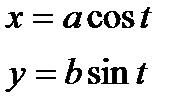
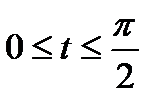 , получим
, получим
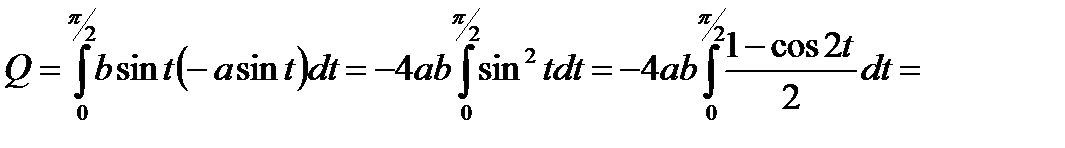
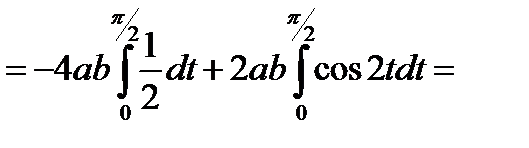
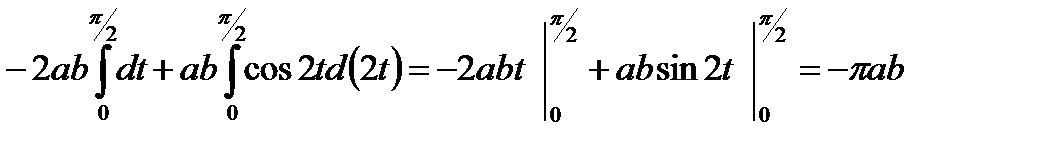
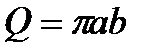 .
.
Дата добавления: 2017-06-13; просмотров: 2494;











