Взаимосвязь понятий «дифференцируемость» и «производная».
Теорема. Если f есть функция одной переменной, т.е. 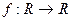 , то существует конечная производная в точке
, то существует конечная производная в точке 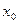
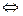 функция дифференцируема в точке
функция дифференцируема в точке 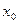 .
.
Доказательство. Необходимость.
Пусть существует производная в точке, 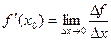 . Докажем, что функция дифференцируема. Если
. Докажем, что функция дифференцируема. Если 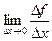 равен числу
равен числу 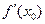 , то сама эта функция, которая под знаком предела, представима в виде: это число + какая-то бесконечно малая.
, то сама эта функция, которая под знаком предела, представима в виде: это число + какая-то бесконечно малая. 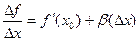 .
.
Если домножить на 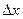 то
то 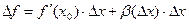 . Здесь обозначим
. Здесь обозначим 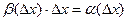 , причём эта
, причём эта 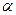
более высокого порядка, ведь на уже существующую бесконечно-малую домножается ещё одна, а именно 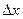 , т.е. порядок возрастает на 1. Получили
, т.е. порядок возрастает на 1. Получили 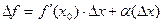 . Определение дифференцируемости выполняется.
. Определение дифференцируемости выполняется.
Достаточность. Пусть f дифференцируема. Выполняется равенство 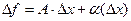 . Разделим его на
. Разделим его на 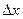 : получим
: получим 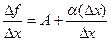 . Перейдём к пределу.
. Перейдём к пределу. 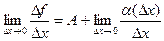 .
.
Но ведь 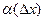 - бесконечно малая более высокого порядка, то есть там содержится
- бесконечно малая более высокого порядка, то есть там содержится 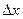 не в первой, а какой-то более высокой степени. Тогда
не в первой, а какой-то более высокой степени. Тогда 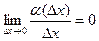 . Осталось
. Осталось 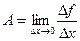 . Заодно доказали, что константа А в этом равенстве - это и есть производная в точке, то есть
. Заодно доказали, что константа А в этом равенстве - это и есть производная в точке, то есть 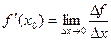 .
.
Замечание. В одном из прошлых примеров, а именно 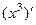 , элемент
, элемент 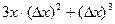 это и есть та самая бесконечно малая более высокого порядка
это и есть та самая бесконечно малая более высокого порядка 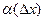 . Здесь она содержит 2 и 3 степени, и как видно, даже после деления на
. Здесь она содержит 2 и 3 степени, и как видно, даже после деления на 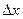 она станет
она станет 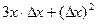 , то есть содержит в каждом слагаемом хоть какие-то степени от
, то есть содержит в каждом слагаемом хоть какие-то степени от 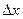 , и поэтому стремится к 0.
, и поэтому стремится к 0.
Лекция № 12. 25. 11. 2016
Основные правила дифференцирования.
Сумма и разность: 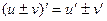 .
.
Произведение: 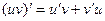 . Частное:
. Частное: 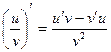 .
.
Композиция: 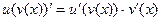 .
.
Запомнить можно так: для произведения между 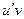 и
и 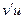 знак плюс, а для частного минус. Но в формуле частного есть ещё лишнее v2 в знаменателе. Почему же производная произведения это не просто
знак плюс, а для частного минус. Но в формуле частного есть ещё лишнее v2 в знаменателе. Почему же производная произведения это не просто 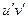 ? И откуда появляется ещё и v2 в знаменателе для частного? Эти формулы вовсе не являются очевидными. Сейчас докажем формулы для произведения и частного.
? И откуда появляется ещё и v2 в знаменателе для частного? Эти формулы вовсе не являются очевидными. Сейчас докажем формулы для произведения и частного.
Доказательство формулы 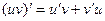 .
.
Запишем производную по определению.
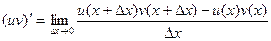
Но тут есть сдвиг на 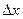 и по u, и по v. Добавим и вычтем такое слагаемое, в котором сдвиг по одной функции есть, а по второй нет:
и по u, и по v. Добавим и вычтем такое слагаемое, в котором сдвиг по одной функции есть, а по второй нет:
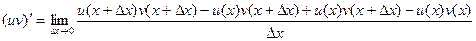 теперь слагаемых стало 4, но зато их можно сгруппировать по два, и даже разбить на две дроби, так, что дельта прибавляется только на одном из мест.
теперь слагаемых стало 4, но зато их можно сгруппировать по два, и даже разбить на две дроби, так, что дельта прибавляется только на одном из мест.
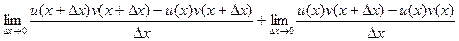
Теперь можно вынести тот множитель, который одинаков в каждой разности:
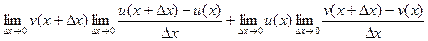
Видно, то, что осталось в дробях, это и есть производные для u или v соответственно, т.е. в итоге:
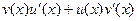 . Итак,
. Итак, 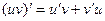 .
.
Докажем формулу 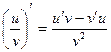 .
.
Запишем по определению: 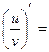
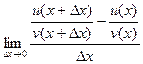 .
.
В том выражении, которое есть в числителе, приведём к общему знаменателю.
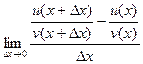 =
= 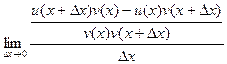 =
=
= 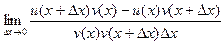 .
.
Аналогично как в прошлом случае, добавим и вычтем слагаемое, чтобы получилось 4 слагаемых а не два, и чтобы в каждой паре был сдвиг только по одной из функций. Можно для этой цели прибавить и отнять, например, 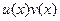 .
.
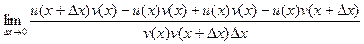 =
=
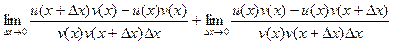
Если во втором пределе переставить два слагаемых и при этом, конечно, добавить знак минус, то часть, содержащая дельта-икс, получится раньше, что и приведёт к записи точь в точь, как в определении производной для v.
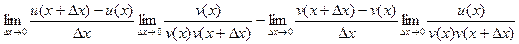 =
=
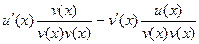 =
= 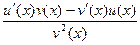 .
.
С помощью правил дифференцирования решим несколько примеров.
Пример.Найти производную тангенса (мы фактически докажем одну из формул таблицы интегралов).
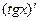 =
= 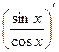 =
= 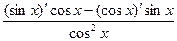 =
= 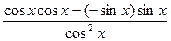 =
= 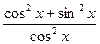 =
= 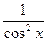 .
.
Итак, 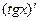 =
= 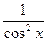 .
.
Пример. Найти 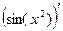 . Примерим формулу дифференцирования композиции.
. Примерим формулу дифференцирования композиции.
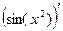 =
= 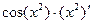 =
= 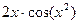 .
.
Дата добавления: 2016-11-29; просмотров: 1934;











