Вычисление длины дуги кривой L, заданной в полярной системе координат.

Пусть кривая L задана в полярной системе координат:

.

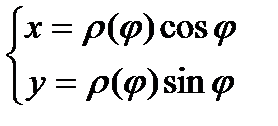
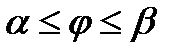Тогда L=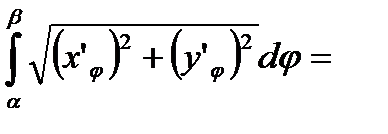

= =

= .

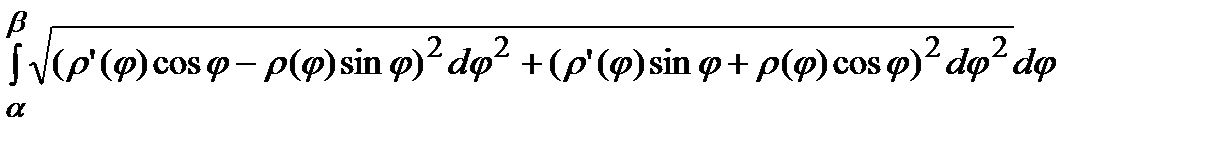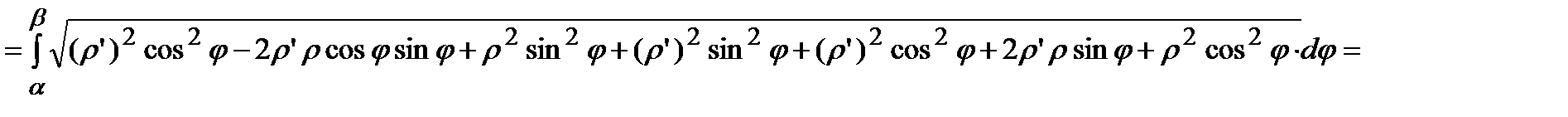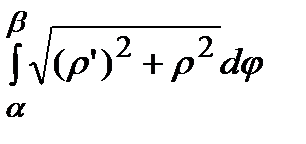Длина дуги кривой в полярной системе координат L= .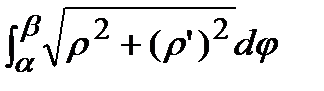

Пример: Вычислить длину кардиоиды .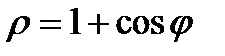

В силу симметричности кривой вычислим ½ длины.

½L= .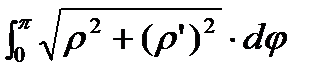

= =

= = = = =

= =

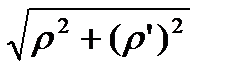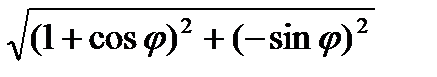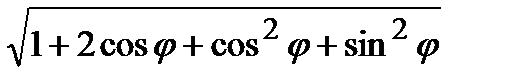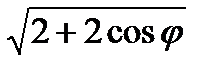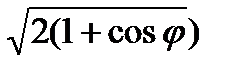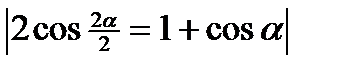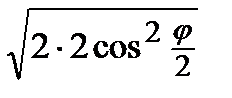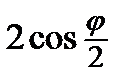
½L= 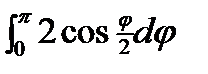= =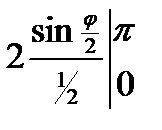4(1-0)=4 ÞL=4∙2=8.

Дифференциал дуги.

Пусть в формуле L= 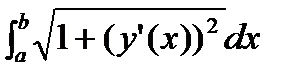для длины дуги нижняя граница остается постоянной, а верхняя граница изменяется. Чтобы подчеркнуть это, обозначим верхнюю границу буквой x, а переменную интегрирования – буквой t. Учтем, что длина дуги L есть функция верхней границы, тогда получим:

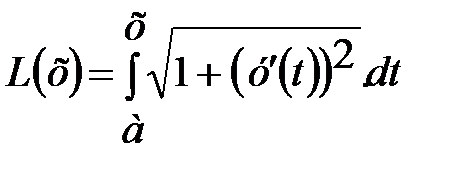
Согласно теореме о производной интеграла по верхней границе эта функция дифференцируема, и ее производная находится по формуле:

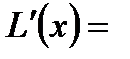
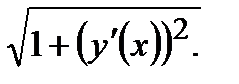
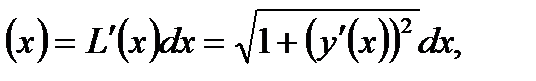
Отсюда дифференциал дуги dL или, в сокращенной записи, dL= 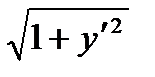dx. Так как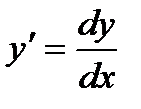 , то dL= 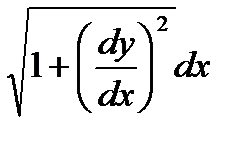, или dL=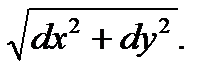

Учитывая полученный результат и то, что дифференциал функции равен приращению ординаты касательной, приходим к следующему геометрическому смыслу дифференциала дуги: дифференциал дуги dL равен длине отрезка касательной от точки касания с абсциссой x до точки с абсциссой x+dx.