Эталоны решения типовых задач
Задача №1. Проводившиеся в некотором районе многолетние наблюдения показали, что из 50000 двадцатилетних граждан до 50 лет доживает в среднем 18120 человек, до 80 лет-724. Найти вероятности для двадцатилетних и пятидесятилетних дожить до 80 лет.
Решение.
Дано: Решение:
n=50000 Вероятность дожить до 80 лет 20-летному гражданину Р(А1)
m1=18120 равна:
m2=724 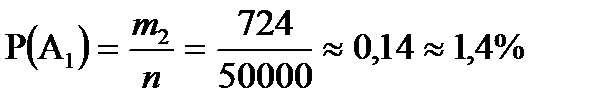
P(A1)-? Вероятность дожить пятидесятилетному до 80 лет Р(А2) равна:
P(A2)-? 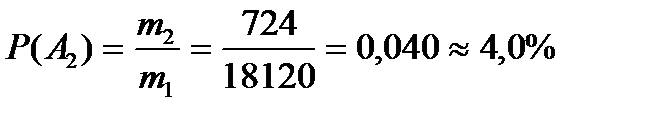
Ответ: P(A1)=1,4% P(A2)= 4%
Задача №2. Вероятность вызова врача в течение часа P(A)=0,47. Найти вероятность, что в течение часа вызова врача не последует.
Дано: Решение:
P(A)=0,47 Сумма вероятностей двух противоположных событий равна 1:
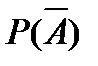 -?
-? 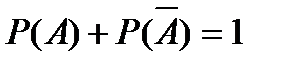
Отсюда: 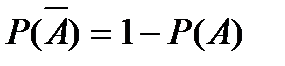
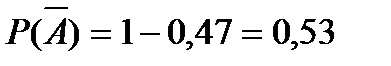
Ответ: 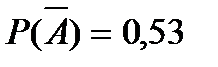
Задача №3. Аптечный склад получает лекарства из городов А,В,С и Д. Вероятность поступления лекарств из города А - Р(А)=0,11; из города В – Р(В)=0,28 и из города Д – Р(Д)=0,32. Найти вероятность поступления лекарств из города С.
Дано: Решение:
P(A)=0,11 Сумма вероятностей событий, составляющих полную
P(В)=0,28 систему, равна единице (условие нормировки)
P(Д)=0,32 P(А)+P(В)+Р(С)+P(Д)=1
P(С)-? Р(С)=1-(Р(А)+Р(В)+Р(Д))=1-(0,11+0,28+0,32)=1-0,71=0,29
Ответ: Р(С)=0,29=29%
Задача №4. На обследование прибыла группа из 50 человек. Семеро из них больны. В кабинет врача приглашали по 2 человека. Найти вероятность того, что:
а) оба больны,
б) оба здоровы,
в) один болен, один здоров.
Дано: Решение:
n=50 а) Пусть Р(А) вероятность того, что первый
m=7 вошедший болен, а Р(В) – второй вошедший болен. Р(А и В)-? Р(А и В, или С и Д)-? События А и В зависимые.
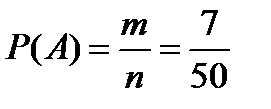
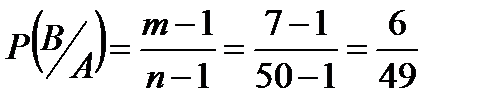
Р(А и В)=Р(А) 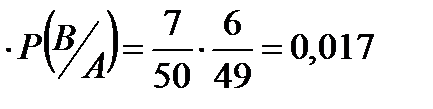

б) А- первый здоров, В-второй здоров.
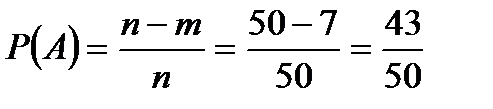
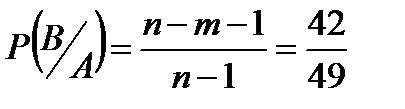
Р(А и В)=Р(А) 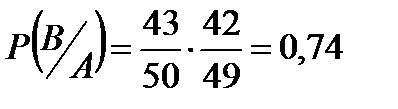
в) Первая ситуация:
А-первый болен, В- второй здоров
Р(А)= 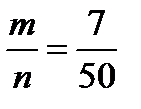
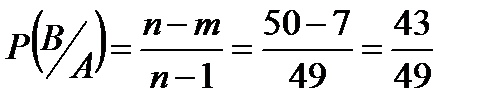
Р(А и В)=Р(А) 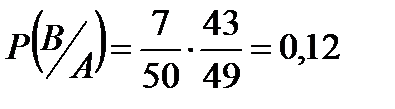
Вторая ситуация:
С-первый здоров, Д- второй болен
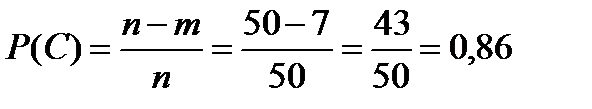
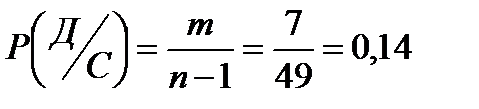
Р(С и Д)=Р(С) 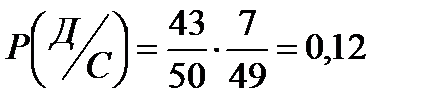
Общая вероятность равна:
Р(А и В, или С и Д)=Р(А и В)+Р(С и Д)=0,12+0,12=0,24
Ответ: а. Р(А и В)=0,017
б. Р(А и В)=0,74
в. Р(А и В, или С и Д)=0,24
Задача №5. Из 20 ампул с лекарственными препаратами ёмкостью по 2 мл в 5 ампулах количество препарата отличалось от нормы. Какова вероятность, что из трёх наугад взятых ампул хотя бы одна окажется нестандартной?
Дано: Решение:
n=20 Задача решается от противного. Противоположными будут
m=5 события, что во всех трёх ампулах лекраственного препарата
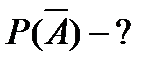 содержится в норме (2мл).
содержится в норме (2мл).
Вероятность, что в первой ампуле содержится норма препарата:
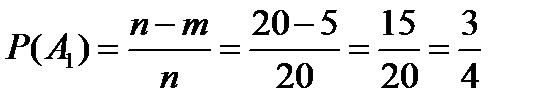 ;
;
во второй:
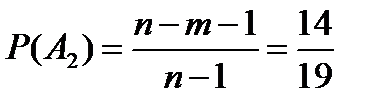 ;
;
в третьей:
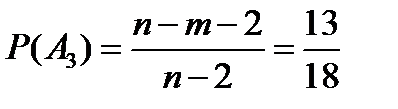 .
.
Вероятность, что во всех трёх ампулах содержится норма лекраственного препарата:
Р(А)=Р(А1 и А2 и А3)=Р(А1)·Р(А2)·Р(А3)= 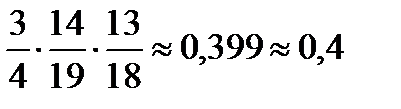
Сумма вероятностей противоположных событий равна единице
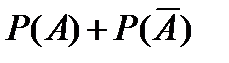 =1
=1
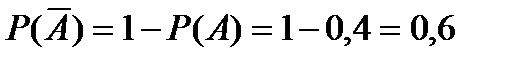
Ответ: 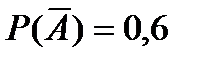
ПРАКТИЧЕСКАЯ ЧАСТЬ
Дата добавления: 2016-06-05; просмотров: 3734;











