Амбиполярная диффузия слабоионизированной плазмы поперек магнитного поля

Рассмотрим плазму, удерживаемую магнитным полемВ = B₀z. Пустьдля простоты плазма имеет форму слоя, неограниченного и однородногов продольных направлениях у и z, с градиентом плотности, направленнымвдоль оси х. В рассматриваемой геометрии диффузия в направлениях уиz не приводит к разделению зарядов. Если толщина плазмы в направлении х меньше дебаевского радиуса, то коэффициенты свободной диффузии будут правильно описывать скорости диффузии ионов и электронов, причем ионы будут диффундировать быстрее электронов, так как D_┴i>>D_┴e. Однако, еcли толщина плазмы в направлении х больше дебаевского радиуса, на диффузию влияют электрические поля, возникающие при стремлении ионов оторваться от электронов. Как и в рассмотренной выше ситуации, эти электрические поля видоизменяют скорости диффузии отдельно для ионов и электронов таким образом, что результирующий поток ионов оказывается равным потоку электронов. Эти потоки имеют вид

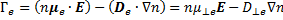
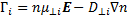
Полагая Г_е = Г_i, можно получить коэффициент амбиполярной диффузии поперек магнитного поля в слабоионизованной плазме, а именно

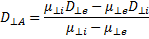(19.1)

В случае сильного магнитного поля ( 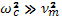) из этого выражения следует, что
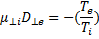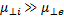и . Таким образом, коэффициент амбиполярной диффузии поперек сильного магнитного поля определяется выражением

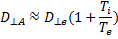(19.2)

Если температуры электронов и ионов одинаковы, то коэффициент амбиполярной диффузии поперек магнитного поля в два раза больше коэффициента свободной диффузии более медленной компоненты, в данном случае электронов. Коэффициент амбиполярной диффузии поперек магнитного поля отличается от коэффициента амбиполярной диффузии в отсутствие магнитного поля. Это отличие состоит в том, что при 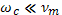имеем D_А = 2D_i, в товремя как при D_⊥A=2D_⊥e.

Диффузия слабоионизованной замагниченной плазмы конечных размеров; эффект короткого замыкания.

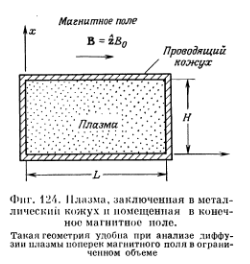
В предыдущем разделе плазма предполагалась ограниченной в направлении х и бесконечной в направлениях у и z. Рассмотрим теперь плазму, ограниченную также в направлении z, совпадающем с направлением магнитногополя В_z (фиг. 124). Пусть плазма находится в идеально проводящем кожухевысотой Н и шириной L, причем L и Н много больше как средней длины свободного пробега между столкновениями, так и дебаевского радиуса.

На основании предыдущего рассмотрения можно было бы ожидать, чтов кожухе с L≈Hплазма будет диффундировать в направлении оси х,т. е. поперек магнитного поля со скоростью, определяемой коэффициентомамбиполярной диффузии D_⊥A=2D_⊥e,а вдоль оси z, т. е. вдоль магнитногополя, со скоростью, определяемой коэффициентом амбиполярной диффузииD_А = 2D_i. Полная диффузия должнатогда представлять сумму этих процессов. Это неверно, поскольку потоки nV_x и nV_zсвязаны друг с другомпосредством уравнения непрерывности 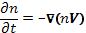. Коэффициент диффузии находится из уравнения непрерывности или уравнения диффузии

,

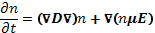которое для электронов имеет вид

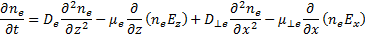(19.3)

и для ионов

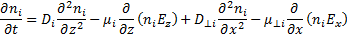(19.4)

Предполагая Е_z ~ Е_х, можно исключить E_z из этих уравнений. Членами с μ_┴eи μ_┴iможно пренебречь на том основании, что подвижностьпоперекВв направлении оси х много меньше подвижности вдоль оси z вследствие того, что млгнитное поле направлено по z, т.е.

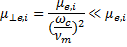(19.5)

Исключая Е_z из уравнений (19.3) и (19.4), получаем уравнение

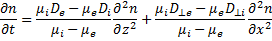(19.6)

Таким образом, коэффициенты диффузии вдоль и поперек магнитного поляне равны друг другу и отличаются от изученных в двух предыдущих случаях,где отношение размеров плазмы вдоль и поперек магнитного поля было оченьбольшим или очень малым. В рассматриваемом случае ограниченной слабоионизованной плазмы эффективные коэффициенты диффузии записываютсяв виде

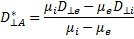(19.7)

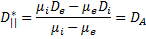(19.8)

Таким образом, эффективный коэффициент диффузии вдоль поля совпадаетс коэффициентом амбиполярной диффузии в отсутствие магнитного поля.Используя неравенства μ_e>>μ_iи D_┴i>>D_┴e, можно упростить выражениедля эффективного коэффициента диффузии поперек поля. В результате получаем приближенное равенство

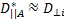(19.9)

которое показывает, что коэффициент диффузии поперек магнитного поляне равен удвоенному коэффициенту диффузии электронов, как предсказывается одномерной моделью, а совпадает с коэффициентом диффузии ионовпоперек магнитного поля. Уравнение диффузии для электронов и ионовпринимает вид

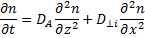(19.10)

Такие значения коэффициентов диффузии получаются потому, чтов одномерных расчетах диффузии вдоль и поперек магнитного поля требовалось, чтобы совпадали объемные потоки ионов и электронов, в то времякак в только что рассмотренной ограниченной задаче требовалось, чтобысовпадали только полные потоки ионов и электронов на стенки. Это означает,что электроны могут двигаться вдоль магнитного поля под действием электрических полей, возникших в процессе ионной диффузии поперек поля. Потокэлектронов на торцевые стенки экспериментальной камеры уменьшает полепространственного заряда, которое препятствовало бы диффузии ионовв одномерной задаче. Таким образом, диффузия ионов поперек поля происходит так, как будто поле пространственного заряда отсутствует. Данное явление называется эффектом короткого замыкания Саймона.

(источник:Н.Кролл, А.Трайвелпис, Основы физики плазмы, гл.6, §11)

Волны в плазме. Электромагнитные волны в плазме. Диэлектрическая проницаемость, дисперсионное уравнение. Низкочастотные волны в плазме. Альфвеновские волны. Ионный звук, пространственная дисперсия. Ленгмюровские волны. Уравнение Власова. Затухание Ландау. Правило обхода Ландау. Понятие о неустойчивостях плазмы. Магнитогидродинамические и кинетические неустойчивости. Пучковая неустойчивость. Квазилинейная теория релаксации. Нелинейные явления в плазме. Понятие о турбулентности плазмы. Аномальные процессы переноса.

Основные понятия и определения

Холодной мы называем плазму, у которой газовое давление мало в сравнении с магнитным

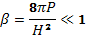
Если это условие выполнено, то при рассмотрении большинства вопросов, относящихся к колебаниям плазмы, можно полностью пренебречь тепловым движением и рассматривать только усредненное движение под действием внешних сил. Будем сначала пренебрегать также столкновениями и всеми процессами, приводящими к затуханию колебаний, т. е. к рассеянию (диссипации) энергии. Такое приближение иногда называют приближением идеальной плазмы. Затухание введем позже как малую поправку.

Теория колебаний холодной плазмы заключается в совместном рассмотрении уравнений движения проводящей среды и уравнений электродинамики Максвелла. Для анализа колебаний уравнения Максвелла удобно преобразовать.

Применяя операции rot к обеим частям уравнения

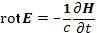(20.1)

получаем

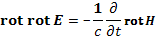
Подстановка сюда уравнения

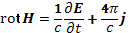(20.2)

дает

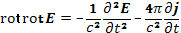
Раскрывая операцию rotrot по формулам векторного анализа, приходим к результату

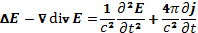(20.3)

Ищем решение в виде плоской волны, распространяющейся вдоль оси х, в которой любая величина f должна зависеть от координаты и времени как

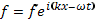(20.4)

где 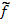— комплексная амплитуда; ω — круговая частота; k — волновое число. Фазовая скорость волны u_ф=ω/k; групповая скорость 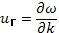. Уравнение, связывающее ω и k, называется дисперсионным уравнением. Показатель преломления N= с/u_ф=kc/ω, где с — скорость света в пустоте. Если фазовая скорость не зависит от частоты (ω: : k), то групповая скорость численно равна фазовой; в этом случае можно говорить просто о скорости распространения волны. Зависимость фазовой скорости от частоты называется дисперсией; она приводит к различию между групповой и фазовой скоростями.

Чтобы определить фазовую и групповую скорости не только по величине, но и по направлению, вводят волновой вектор k, длина которого равна волновому числу, а направ- направление определено таким образом, чтобы в плоской волне любая величина f зависела от координат и времени как

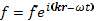(20.4a)

Направление фазовой скорости есть направление волнового вектора, т. е. направление, в котором распространяется определенная фаза волны. В анизотропной среде частота связана не только с величиной, но и с направлением волнового вектора, т. е. дисперсионное уравнение имеет вид

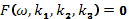
где k_l, k₂, k₃ — составляющие волнового вектора. В результате дифференцирования этого уравнения получим

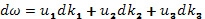
Коэффициенты u₁,u₂, u₃ имеют размерность скорости и рассматриваются как составляющие вектора групповой скорости. В векторной форме

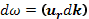
что иногда записывают символически как

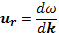
Направление групповой скорости есть направление переноса энергии волной.

В дальнейшем оси координат будем выбирать так, чтобы k₂ = 0. Под k₁ будет пониматься составляющая волнового вектора по нормали к магнитному полю, под k₃ — вдоль поля. В линейном приближении уравнения для комплексных амплитуд 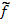имеют такой же вид, как и уравнения для величин f. В дальнейшем не будем делать различия между обозначениями комплексных амплитуд и переменных величин там, где это специально не необходимо. Для плоской волны дифференциальным операторам отвечают алгебраические операции:

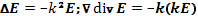
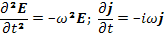
Уравнение (20.3) дает

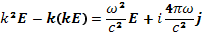(20.5)

Уравнения движения электронов и ионов без учета столкновений и других диссипативных процессов имеют вид:

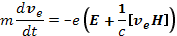(20.6)

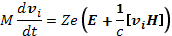(20.7)

Будем рассматривать линейные колебания. Тогда лагранжеву производную d/dt можно заменить частной производной ∂/∂t и в произведении [vH] пренебречь собственным полем волны, т. е. заменить Н на постоянное внешнее полеН_о. В дальнейшем собственное магнитное поле волны, когда оно нам понадобится, будем обозначать 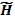. Преобразуем уравнения (20.6) и (20.7) так, чтобы получить уравнения для массовой скорости

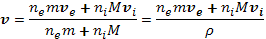(20.8)

и плотноститока

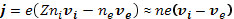(20.9)

При этом будем пользоваться условием квазинейтральности

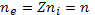(20.10)

и пренебрегать массой электрона m в сравнении с массой иона М. Сложение уравнений (20.6) и (20.7) с весами n_em и n_iМ дает гидродинамическое уравнение

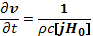(20.11)

Вычитание этих уравнений с пренебрежением членами, содержащими большую массу М в знаменателе, дает уравнение для плотности тока

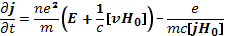(20.12)

Система уравнений (20.11)—(20.12) совпадает с системой уравнений магнитной гидродинамики для идеального проводника, из которых выброшены силы давления. В соответствии с этим приближение холодной плазмы называют иногда гидродинамическим приближением. Удобно ввести характерные частоты плазмы: плазменную частоту

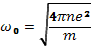(20.13)

и циклотронные частоты

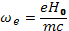(20.14)

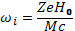(20.15)

Тогда уравнение (20.12) перепишется как

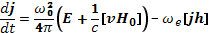(20.16)

гдеh — единичный вектор в направлении постоянного внешнего магнитного поля. Для плоской волны вида (20.4) уравнения (20.11) и (20.16) принимают вид:

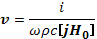(20.17)

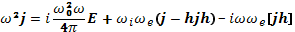(20.18)

В последнем уравнении двойное векторное произведение раскрыто по формуле [А[ВС]]=В(АС)—С(АВ) и использовано соотношение

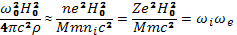(20.19)

Теперь рассмотрение всех типов колебаний холодной плазмы сводится к совместному решению системы уравнений (20.5) и (20.18). При выводе этой системы сделаны следующие допущения:

1) амплитуды всех переменных величин в волне полагаются малыми, чтобы можно было пренебречь всеми квадратичными членами (линейное приближение);

2) тепловое (газовое) давление считается малым в сравнении с магнитным давлением (приближение холодной плазмы);

3) пренебрегается всеми диссипативными процессами, т. е. колебания полагаются адиабатическими. Это приближение иногда называют приближением идеальной плазмы;

4) отбрасываются члены порядка отношения массы электрона к массе иона. Это допустимо, если приближение проведено аккуратно в математическом отношении.

Таким образом, можно сказать, что система (20.5)—(20.18) описывает линейные адиабатические колебания холодной плазмы, или линейные колебания холодной идеальной плазмы.

Кроме того, в настоящей книге речь идет о полностью ионизованной плазме.