Рассеяние (замедление) нейтронов на ядрах среды.

Основным процессом, приводящим к замедлению нейтронов, является упругое рассеяние. Потеря энергии при упругом рассеянии зависит от массового числа ядра замедлителя, начальной энергии нейтрона и угла рассеяния.

При столкновении с ядром нейтрона с энергией в несколько электрон-вольт (эВ) происходит передача части кинетической энергии нейтрона ядру (энергия отдачи). В первом приближении, даже ядра, связанные в молекулах и/или в твердых телах, можно считать свободными и применять методы классической механики, например, рассматривать упругий удар двух тел.

Исходя из нерелятивистских соотношений (скорость нейтрона 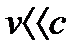, где с – скорость света) - закона сохранения энергии и импульса, записанные в лабораторной системе координат,

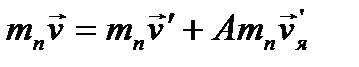
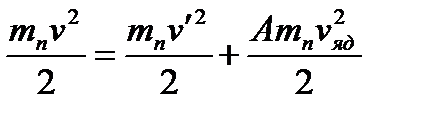
легко получить связь между скоростью (энергией) нейтрона после рассеяния со скоростью (энергией) до рассеяния:

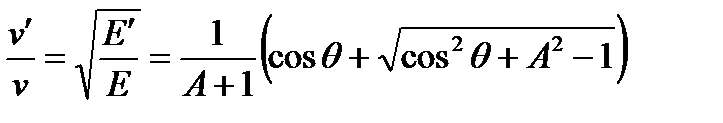
Здесь 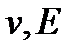- скорость и энергия нейтрона до рассеяния; 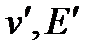- после рассеяния; 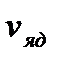-скорость, приобретенная ядром после рассеяния; 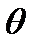- угол рассеяния нейтрона, А – массовое число ядра. В приведенных выше кинематических соотношениях использованы два приближения: 1) ядро до взаимодействия с нейтроном покоится (учет теплового движения и химических связей является отдельной сложной задачей); 2) масса ядра полагается равной сумме масс внутриядерных нуклонов (здесь разницей между массами нейтронов и протонов пренебрегается, т.е. .)

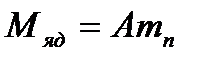Максимальное уменьшение энергии нейтрона для всех ядер-мишеней, кроме водорода происходит в случае лобового удара ( ):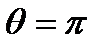

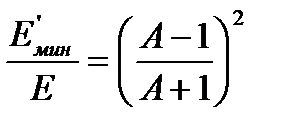
Видно, что потери энергии нейтроном в одном акте рассеяния тем больше, чем легче ядро-мишень. Отсюда же видно, что в случае водорода (А=1)

,

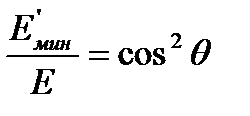а предельный угол рассеяния нейтрона равен 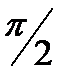. При рассеянии на угол 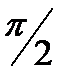нейтрон останавливается, передавая ядру водорода всю энергию. Таким образом, водород является самым эффективным замедлителем нейтронов.

Диапазон энергий, в котором будет находиться энергия нейтрона после рассеяния можно записать в виде

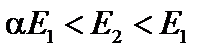, (4.21)

где параметр a определяет максимальную долю потерю энергии при упругом рассеянии. Диапазон энергий (4.21), в котором находится энергия нейтрона после единичного акта упругого рассеяния, называют ступенькой замедления, 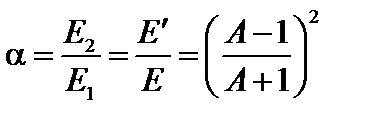.Чем тяжелей ядро (чем больше А), тем меньшая часть энергии теряется нейтроном, тем меньше ступенька замедления.

Закон упругого замедления нейтронов: в результате однократного упругого рассеяния нейтрон с равными вероятностями приобретает любую энергию в пределах ступеньки замедления. В качестве характеристики потерь энергии нейтрона в одном столкновении принято использовать величину, называемую средней логарифмической потерей энергии, которая определяется как

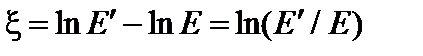. (4.41)

где E`,E – энергия нейтрона до и после взаимодействия соответственно. Среднелогарифмическая потеря энергии 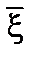не зависит от начальной энергии нейтрона.

Значение средней логарифмической потери энергии для водорода равна 1, с увеличением А быстро падает. Для расчета 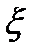обычно используется формула:

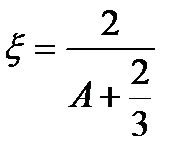
Для удобства вычислений вводится еще одна безразмерная величина – летаргия – величина, увеличивающаяся при уменьшении энергии нейтрона в процессе замедления

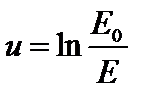. (4.45)

Удобство использования летаргии заключается в том, что при уменьшении энергии нейтрона в процессе замедления:

- ширина ступеньки замедления DЕ по шкале энергии уменьшается:

;

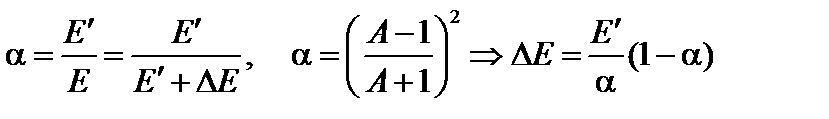- ширина ступеньки Dи по шкале летаргии не изменяется (постоянна):

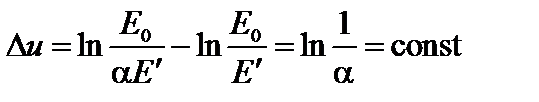. (4.46)

Используя среднее логарифмические потери энергии на одно столкновение, можно легко посчитать число столкновений (n), необходимое нейтрону, чтобы замедлиться от энергии Е_нач до Е_кон:

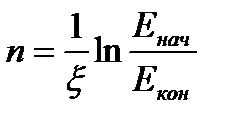
Используя введенную выше энергетическую переменную – летаргию, полное число столкновений нейтронов в интервале энергий от Е_нач(u_нач) до Е_кон (u_кон), можно записать как

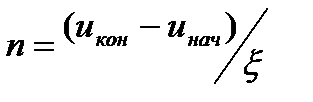
Очевидно, зная 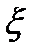можно легко решить и обратную задачу – определить энергию нейтрона (Е_n) после n-го столкновения:

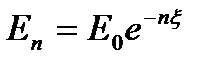
Знания среднелогарифмических потерь энергии в одном столкновении недостаточно, чтобы судить о качестве материала как замедлителя. Значительно полнее характеризует замеляющие свойства вещества параметр, учитывающий наряду с потерями энергии в столкновении и среднее число столкновений нейтрона на единице пути. Таким параметром является произведение 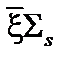. Величина 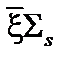определяет среднюю логарифмическую потерю энергии нейтрона при прохождении им 1 см пути в веществе - Замедляющая способность.

Замедляющая способность 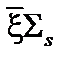[см^-1] является величиной, полностью характеризующей замедляющие свойства среды (вещества).

Замедляющую способность сплавов или химических соединений рассчитывают по формуле

.

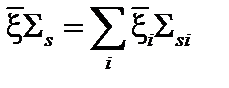Коэффициентом замедления называется безразмерная величина, равная отношению замедляющей способности среды и эффективного макросечения поглощения среды (вещества):

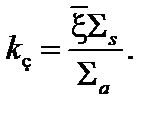
Коэффициент замедления служит показателем соотношения замедляющих и поглощающих свойств.

Оптимальный замедлитель должен обладать следующими ядерными свойствами:

· большим сечением рассеяния (Σs);

· небольшим сечением поглощения (Σа);

· способностью максимально уменьшать энергию нейтрона в одном столкновении.