Амбиполярная диффузия

Рассмотрим заполненную газом полость, в которой к стенкам диффундируют как ионы, так и электроны. Как правило, в такого рода задачах можно пренебречь взаимодействием положительно и отрицательно заряженных частиц при плотностях последних ниже 10⁷—10⁸ см^-3; при больших степенях ионизации влияние объемного заряда из-за кулоновского взаимодействия электронов с положительными ионами начинает играть важную роль, и этот эффект нельзя не учитывать.

Можно показать, что в сильно ионизованном газе плотность электронов приблизительно равна плотности положительно заряженных ионов в любой точке, за исключением области вблизи границы, газа с поверхностью, толщина которой порядка дебаевского радиуса экранирования[14]. Любое отклонение распределения зарядов от нейтрального приводит к появлению электростатических сил, препятствующих разделению зарядов и стремящихся вернуть нарушенное равновесие. Вследствие того, что коэффициент диффузии электронов значительно больше коэффициента диффузии ионов, электроны быстрее ионов диффундируют в области с меньшей концентрацией зарядов, однако их движение замедляется полем возникающего пространственного заряда. Это же поле ускоряет ионы, заставляя их диффундировать быстрее, чем в отсутствие электронов. В итоге заряженные частицы обоих знаков диффундируют с одинаковой скоростью, и, поскольку в потоках частиц противоположных знаков различия нет, такая диффузия зарядов носит название «амбиполярной». Понятие амбиполярной диффузии было введено Шоттки в 1924 г. при исследовании положительного столба тлеющего разряда.

Теперь мы выведем выражение для коэффициента амбиполярной диффузии. Пусть общая плотность электронов и положительных ионов равна п, a v_a — скорость амбиполярной диффузии. Предположим далее, что давление газа достаточно высоко для того, чтобы частицы часто испытывали столкновения. Тогда понятие подвижности применимо не только для ионов,но и для электронов. Предположим, что в результате разделения зарядов возникает электрическое поле 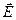. Поскольку скорость диффузии для частиц обоих знаков одинакова, мы имеем

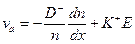
и

,

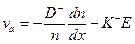где K⁺ и K^- — подвижности ионов и электронов соответственно,
D⁺ и D^- — их обычные, или «свободные», коэффициенты диффузии.

Все четыре коэффициента являются положительными числами. Исключая E из написанных уравнений, находим

,

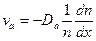где D_a — коэффициент амбиполярной диффузии, определяемый выражением

.

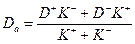Коэффициент D_a характеризует диффузионное движение частиц обоих знаков.

Если предположить, что 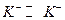и , и 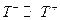использовать соотношение Эйнштейна : 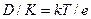, то в результате получим

.

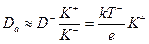С другой стороны, при 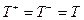найдем, что

.

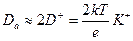В случае амбиполярной диффузии частиц нестационарное уравнение диффузии, имеет вид

.

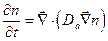Если предположить, что D_a не зависит от координаты, а плотность числа частиц затухает как 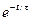, то стационарное уравнение амбиполярной диффузия запишется в форме

.

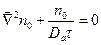Для ряда частных случаев коэффициент D_a определяется через постоянную времени затухания τ и длину диффузии 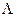согласно равенству

.

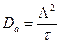Мы видим, таким образом, что коэффициент амбиполярной диффузии D_a можно рассчитать на основе данных о скорости распада заряженных частиц в плазме после выключения источника ионизации. В случае равенства температур электронов, ионов и нейтральных частиц газа из уравнения следует, что коэффициент диффузии и подвижность ионов могут быть определены на основе измерений коэффициента D_a . Приведенная подвижность ионов K₀ при нулевом поле связана с коэффициентом амбиполярной диффузииD_a уравнением

.

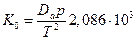Здесь давление р измеряется в мм рт.ст., а температура Т, при которой определяется коэффициент D_a, — в кельвинах; наконец, приведенная подвижность K₀ выражается в единицах см²/(В×с), а D_a — в единицах см²/с.

3 Кинетическая теория диффузии и подвижности ионов