ЭДС взаимной индукции

ЭДС, индуктируемые в первом и втором контурах, с учетом (2.48, 2.49) можно записать в виде

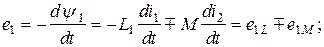
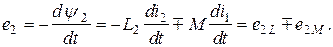
Таким образом, ЭДС каждой катушки определяется алгебраической суммой ЭДС самоиндукции и взаимной индукции. Для определения знака ЭДС взаимной индукции размечают зажимы индуктивно связанных элементов цепи. Два зажима называют одноименными, если при одинаковом направлении токов относительно этих зажимов магнитные потоки самоиндукции и взаимной индукции складыва­ются. Такие выводы обозначают на схемах одинаковыми условными значками, например, точками или звездочками (рис. 2.20 а, б). 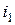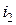Одинаково направленные токи и (рис. 2.20 а) относительно зажимов 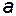и 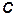вызывают совпадающие по направлению потоки самоиндукции 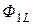( 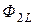) и взаимной индукции 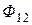( 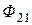). Следовательно, зажимы 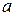и 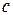являются одноименными. 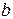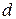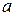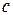Одноименной является и другая пара зажимов и , но условными значками обозначают только одну пару одноимен­ных выводов, например, и (рис. 2.20 а). Если ток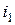и и 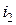направ­лены неодинаково относительно одноименных зажимов (рис. 2.20 б), то имеет место встречное направление потоков самоиндукции и взаимоиндукции.

На схемах магнитопроводы, как правило, не показывают и ограничиваются только обозначением одноименных зажимов (рис. 2.20 в, г).

Одноименные зажимы можно определить опытным путем. Для этого одну из катушек включают в цепь источника постоянного тока, а к другой присоеди­няют вольтметр постоянного тока. Если в момент подключения ис­точника стрелка измерительного прибора отклоняется, то зажимы индуктивно связанных

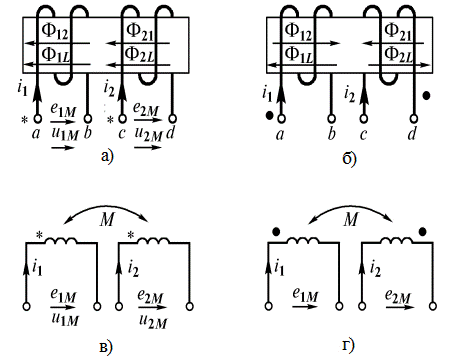
Рис. 2.20

катушек, подключенные к положительному полюсу источника и поло­житель­ному зажиму измерительного прибора, являются одноименными.

Определим знаки ЭДС и напряжения взаимной индукции. Допустим, пер­вая катушка (рис. 2.20 а) разомкнута, а во второй протекает ток . Выберем поло­жительные направления для 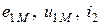одинаковыми относительно одноимен­ных зажимов. ЭДС и напряжение взаимной индукции равны, но противоположны по знаку. Действительно, когда 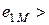0, потенциал зажима b больше потенциала зажима а, следовательно, 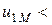0.

По правилу Ленца знак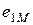и и 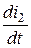всегда противоположны, поэтому

.

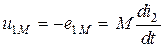В комплексной форме уравннеие имеет вид

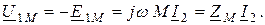(2.50)

При встречном включении катушек (рис. 2.20 б)

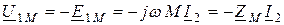. (2.51)

Из (2.50) и (2.51) видно, что вектор напряжения на взаимной индуктивности 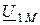сдвинут по фазе относительно вектора тока 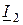на угол ±90°.

Сопротивление 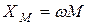называется сопротивлением взаимной индуктивно­сти, а 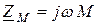– комплексным сопротивлением взаимной индуктивно­сти.

Таким образом, при согласном направлении токов падение напряжения на взаимной индуктивности имеет знак «плюс», при встречном – знак «минус».

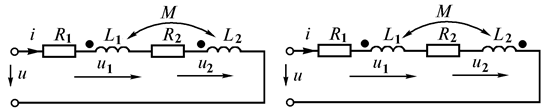
2.6.3. Последовательное соединение двух индуктивно связанных
катушек

Рассмотрим две катушки, соединенные последовательно и имеющие актив­ные сопротивления 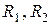, индуктивности 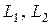и взаимную индуктивность 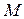. Возможны два вида их включения – согласное (рис. 2.21 а) и встречное (рис. 2.21 б). При согласном включении ток в обеих катушках направлен одинаково относи­тельно одноименных зажимов, поэтому падение напряжения на взаимной индук­тивности в уравнениях Кирхгофа для мгновенных значений запишем со знаком «плюс»

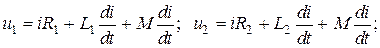
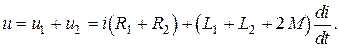
Эти же уравнения в комплексной форме

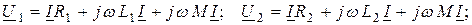
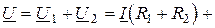
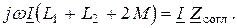(2.52)

а) б)

Рис. 2.21

Полное сопротивление цепи при согласном включении

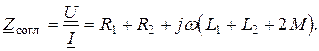
При встречном включении (рис. 2.21 б) ток в катушках направлен противопо­ложно относительно одноименных зажимов, поэтому напряжения на взаимной индуктивности записывают со знаком «минус». В этом случае уравне­ния Кирхгофа в комплексной форме имеют вид

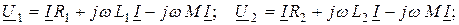
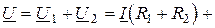
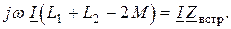(2.53)

Полное сопротивление цепи при встречном включении

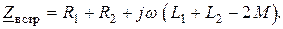
Полное сопротивление цепи при согласном включении больше, чем при встречном. Этим можно пользоваться для определения опытным путем одно­именных зажимов индуктивно связанных катушек.

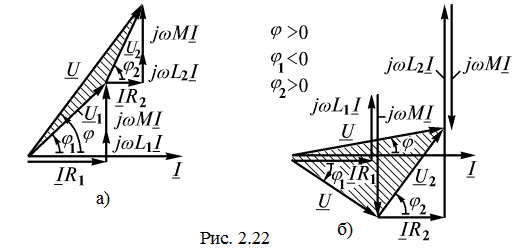
На рис. 2.22 построены векторные диаграммы для согласного и встречного включения катушек. Начальная фаза вектора тока, являющегося общим для всех элементов цепи, принята равной нулю. По вектору тока сориентированы в по­рядке записи все слагаемые напряжени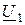й и 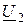(2.52, 2.53). Упрощает выбор направления векторов правило о том, что умножение комплекса на 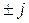соответст­вует его повороту на ± 90°. Многоугольники векторов 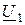, , 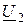, 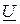построенные на диаграмме соответственно с законом Кирхгофа, для наглядности заштрихо­ваны.

Векторная диаграмма (рис. 2.22 б) при встречном включении катушек по­строена в предположении, что 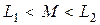. При таком соотношении параметров в первой катушке наблюдается емкостный эффект, т.к. напряжение 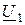отстает от тока 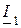. В цепи нет конденсаторов, но индуктивность первой катушки 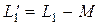получается отрицательной, что равноценно включению конденса­тора. Однако в целом цепь всегда имеет индуктивный характер, т.к. вектор тока отстает от вектора напряжения на входе в виду того, что .

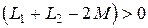При согласном включении катушек емкостный эффект невозможен.