Мощности в комплексной форме

Формулы для определения полной, активной и реактивной мощностей записаны раньше

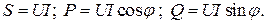
Рассмотрим простой прием, позволяющий найти активную и реактивную мощности по комплексным напряжению и току. Для этого умножим комплекс напряжения на сопряженный комплекс тока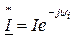

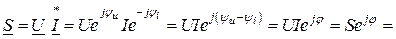
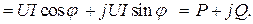(2.46)

Полученное значение 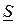называют комплексом полной мощности. Из (2.46) видно, что вещественная часть комплексной мощности равна активной мощности, мни­мая часть – реактивной:

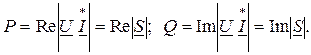(2.47)

Пример 2.4. Определить активную, реактивную и полную мощности, если мгновенные значения тока и напряжения заданы уравнениями

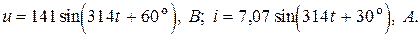
Решение. Запишем комплексы действующих значений напряжений и тока

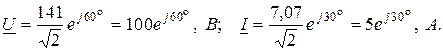
Комплекс полной мощности

+

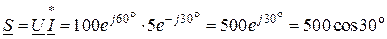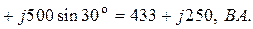
Таким образом, 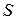= 500 ВА, 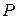= 433 Вт, 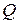= 250 вар.

2.5. Повышение коэффициента мощности в цепях синусоидального
тока

Большинство современных потребителей электрической энергии имеют ин­дуктивный характер нагрузки, токи которой отстают по фазе от напряжения ис­точника. Активная мощность таких потребителей при заданных значениях тока и напряжения зависит от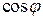

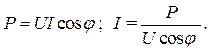
Следовательно, повышение коэффициента мощности приводит к уменьше­нию тока.

Если обозначить сопротивление проводов линии 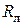, то потери мощности в ней можно определить так:

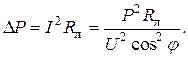
Таким образом, чем выше 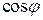потребителя, тем меньше потери мощности в линии и дешевле передача электроэнергии. Коэффициент мощности показывает, как используется номинальная мощность источника. Так, для питания приемника 1000 кВт при 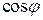= 0,5 мощность генератора должна быть

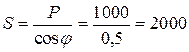кВА,

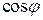а при = 1 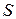= 1000 кВА.

Следовательно, повышение 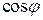увеличивает степень использования мощно­сти генераторов. Чтобы повысить экономичность энергетических устано­вок, принимают повышают 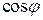– используют батареи конденсаторов, подключаемые параллельно индуктивной нагрузке (рис. 2.18 а).

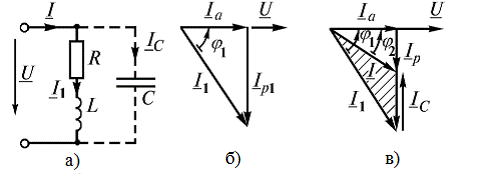
Рис. 2.18

Емкость конденсатора, необходимую для повышения 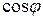от существующего зна­чения 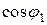до требуемого , можно определить по диаграмме (рис. 2.18 б, в). При построении векторной диаграммы в качестве исходного вектора принят вектор напряжения источника. Если нагрузка представляет собой индуктив­ный характер, то вектор тока 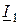отстает от вектора напряжения на угол 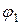. Актив­ная составляющая тока 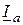совпадает по направлению с напряжением, реак­тивная составляющая тока 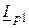отстает от него на 90° (рис. 2.18 б).

После подключения к потребителю батареи конденсаторов ток 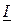определя­ется как геометрическая сумма векторов 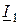и 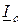. При этом вектор емкост­ного тока 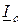опережает вектор напряжения на 90° (рис. 2.18 в). Из вектор­ной диаграммы видно, что 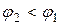, т.е. после включения конденсатора коэффици­ент мощности повышается от 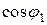до .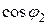

Емкость конденсатора можно рассчитать при помощи вектор­ной диаграммы токов (рис. 2.18 в)

.

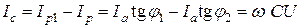Учитывая, что 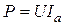, запишем емкость конденсатора

.

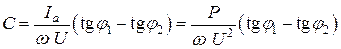На практике обычно коэффициент мощности повышают не до 1,0, а до 0,90...0,95, так как полная компенсация требует дополнительной установки кон­денсаторов, что часто экономически не оправдано.

2.6. Электрические цепи с взаимной индуктивностью

Общие сведения

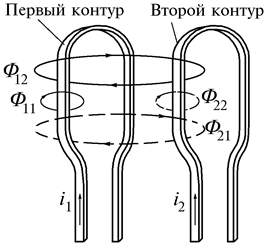Рис. 2.19

При рассмотрении цепей синусоидального тока до сих пор учитывалось только явле­ние самоиндукции катушек, обусловлен­ное током в цепи. Цепи, в которых наво­дятся ЭДС между двумя (и более) взаимно связанными катушками, называются индуктивно связанными цепями.Рассмот­рим явление возникновения ЭДС в одном из контуров при изменении тока в другом.

Контуры (рис. 2.19) представляют собой плоские тонкие катушки с числами витков 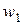и 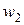. Поток самоиндукции 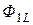, созданный то­ком 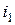, может быть представлен в виде потока рассеяния 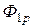, пронизывающего только пер­вый контур, и потока 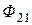, пронизывающего второй контур

= + .

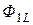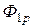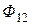Аналогично определяем поток самоиндукции второго контура

= + .

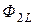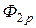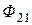Поток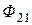и и 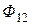называют потоками взаимной индукции. Их принято обо­значать двумя индексами: первый индекс указывает, с каким контуром сцепляется поток, второй – номер тока, вызвавшего данный поток. Например, поток 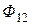вы­зван током 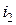, сцепляется с первым контуром. Если направление потока взаимной индукции совпадает с направлением потока самоиндукции данного контура, то говорят, что магнитные потоки и токи контуров направлены согласно. В случае противоположного направления говорят о встречном направлении потоков. Суммарные потоки, пронизывающие первый и второй контуры

= ± ; = ± ,

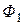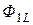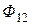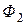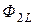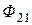где «+» соответствует согласному направлению потоков, «–» – встречному на­правлению.

Полные потокосцепления первого и второго контуров

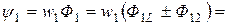
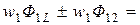
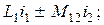(2.48)

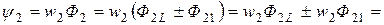
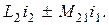(2.49)

Отношение потокосцепления взаимной индукции в одной цепи к току в дру­гой называется взаимной индуктивностью

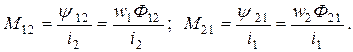
Для линейных электрических цепей всегда выполняется равенство

.

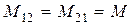Взаимная индуктивность двух катушек зависит от числа витков, геометри­ческих размеров магнитопровода и взаимного расположения катушек, а также от абсолютной магнитной проницаемости среды (материала магнитопровода). Ин­дуктивную связь двух катушек характеризуют коэффициентом связи

.

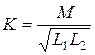Этот коэффициент всегда меньше единицы, так как магнитный поток взаим­ной индукции всегда меньше потока самоиндукции и может быть увеличен за счет уменьшения потоков рассеяния бифилярной намоткой катушек (двойным проводом) или применением для магнитопровода материала с высокой абсолют­ной магнитной проницаемостью.