Мощности цепи синусоидального тока

Энергетические соотношения в отдельных элементах 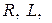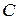рассматрива­лись в предыдущей теме. Рассмотрим участок электрической цепи, напряжение на котором 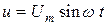, а ток .

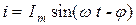Определим мгновенную мощность

.

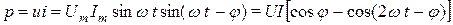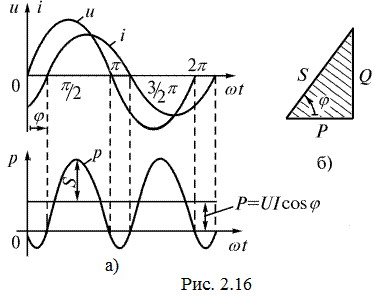
Полученное уравнение со­держит две составляющие: по­стоянную и синусоидальную, имеющую удвоенную частоту по сравнению с частотой тока и на­пряжения. Мгновенные значения тока, напряжения и мощности при индуктивном характере цепи ( 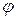> 0) показаны на рис. 2.16 а.

В промежутках времени, когда 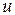и и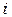меют одинаковые знаки, мгновенная мощность положительна, энергия посту­пает от источника в приемник, потребляется резистором и запасается в магнитном поле катушки. Когда же 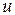и 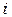имеют разные знаки, мгновенная мощность отрица­тельна и энергия частично возвращается от приемника к источнику. Ак­тивная мощность, поступающая в приемник, равна среднему значению мгно­венной мощности за период

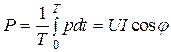
. (2.33)

Тригонометрическая функция 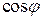называется коэффициентом мощности. Как видно из (2.33), активная мощность равна произведению действующих значений напряже­ния и тока, умноженному на коэффициент мощности. Чем ближе угол 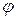к нулю, тем ближе 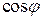к единице и, следовательно, тем большая при заданных значе­ниях напряжения и тока активная мощность передается от источника к нагрузке.

Формулу активной мощности можно преобразовать с учетом полученных ранее соотношений

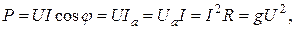Вт. (2.34)

Произведение действующих значений тока и напряжения на входе цепи назы­вается полной мощностью и измеряется в вольт-амперах (ВА)

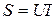. (2.35)

Графически полная мощность характеризует амплитуду колебаний мгновен­ной мощности относительно средней (активной) мощности (рис. 2.16 а). Полная мощ­ность является расчетной мощностью электрических установок (генераторов, трансформаторов и др.), для которых она указывается в качестве номинальной, например, для генератора номинальная (полная) мощность равна его активной максималь­ной мощности, которая может быть получена при 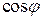= 1. Однако для большинства потребителей 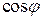< 1. Поэтому даже при номинальных значениях напряжения и тока энергетические возможности источника используются не пол­ностью, так как .

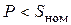При расчетах электрических цепей и эксплуатации электрооборудования пользуются также понятием реактивной мощности, которая вычисляется по формуле

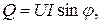вар. (2.36)

Реактивная мощность характеризует собой энергию, которой обмениваются генератор и приемник. Она определяется максимальным значением мощности на участке цепи с реактивными элементами

.

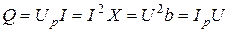Реактивная мощность цепи может быть положительной и отрицательной в зависимости от знака угла 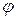. При индуктивном характере входного сопротивле­ния ( 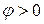) реактивная мощность положительна, при емкостном характере ( 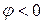) – отрицательна.

Сравнив формулы (2.34)...(2.36), нетрудно установить связь между актив­ной, реактивной и полной мощностями

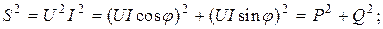
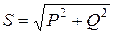. (2.37)

Соотношение (2.37) удобно представить в виде прямоугольного треуголь­ника мощностей (рис. 2.16 б), который можно получить из треугольника напря­жений умножением сторон на ток. Из треугольника мощностей имеем соотноше­ния, широко используемые при расчетах

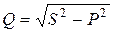; tgj = Q/P; cosj = P/S. (2.38)

Активная мощность, потребляемая приемником, не может быть отрицатель­ной, поэтому всегда 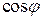> 0, т. е. на выходе цепи 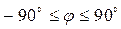. Активная мощность отображает совершаемую работу или передаваемую энер­гию в единицу времени.