Комплексный метод расчета цепей синусоидального тока

Широкое распространение на практике получил метод расчета цепей синусои­дального тока, который принято называть комплексным. Сущность ме­тода состоит в том, что синусоидальные токи, напряжения и ЭДС изображаются комплексными числами, а геометрические операции над векторами заменяются алгебраическими операциями над комплексными числами. Этот метод позволяет рассчитывать цепи синусоидального тока алгебраически аналогично цепям посто­янного тока.

2.4.1. Векторное представление синусоидальных величин

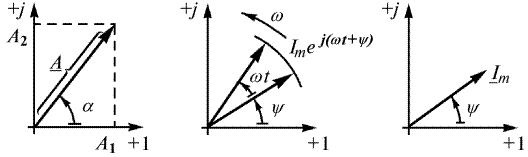
Вращающийся вектор, который изображает синусоидальную функцию, можно поместить на комплексную плоскость, в систему перпендикулярных осей: 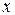– действительных чисел, 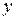– мнимых чисел. Положительные направления осей на комплексной плоскости обозначаются индексами: +1 – ось действительных чи­сел; + 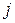– ось мнимых чисел, где 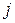= 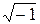– мнимая единица (рис. 2.17).

а) б) в)

Рис. 2.17

Известно, что координаты точки на комплексной плоскости определяются радиусом–вектором этой точки, т.е. вектором, начало которого совпадает с нача­лом координат, а конец находится в точке, соответствующей заданному ком­плексному числу (рис. 2.17 а).

Показательная форма записи

,

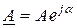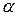где – модуль; – аргумент или фаза, отсчитываемая от оси +1 против часовой стрелки.

Применив формулу Эйлера, можно получить тригонометрическую и соответ­ственно алгебраическую форму записи комплексного числа:

,

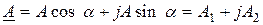где ; .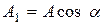

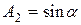Очевидно

; .

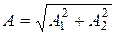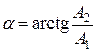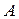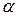Заменим в уравнении для показательной формы записи на , а на 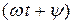. Получим комплекс тока

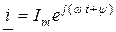, (2.39)

который является символическим (комплексным) изображением функции 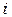и называется комплекс мгновенного значения тока.

Комплексы обозначаются теми же буквами, что и их действительные ориги­налы, только с чертой внизу. Модуль комплекса мгновенного значения 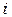равен амплитуде синусоидального тока 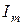, а его переменный аргумент ( 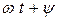) явля­ется аргументом изображаемой синусоиды (рис. 2.17 б). Из формулы (2.39) можно записать комплекс тока в тригонометрической форме

,

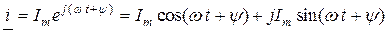а также получить изображение функции (оригинала)

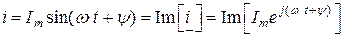, (2.40)

т.е. мгновенное значение тока равно мнимой части комплекса мгновенного значе­ния тока. Ток (2.39) можно представить в виде

,

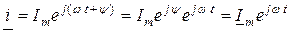где 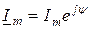является другим символом, называемым комплексом амплитуд­ного значения. Это аналитическое представление неподвижного вектора, длина которого равна амплитуде тока, а угол между направлениями вектора и осью «+1» на комплексной плоскости равен начальной фазе 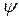(рис. 2.17 в). Комплексом дейст­вующего значения называют изображение

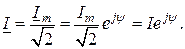
Пример 2.2. Записать комплексы действующих значений напряже­ния и тока, если их мгновенные значения представлены уравнениями

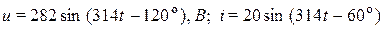, А.

Решение. Действующее значение напряжения 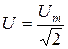=200 В, начальная фаза 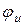= –120°. В соответствии с определением комплекс действующего значе­ния напряжения

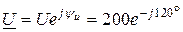В.

Аналогично для тока 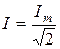= 14,1 А, начальная фаза тока 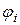= –60°, а ком­плекс ток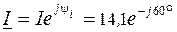а

А.

Пример 2.3. Для комплекса действующего значения напряжения

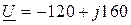B

записать мгновенное значение.

Решение. От алгебраической формы переходим к показательной

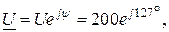B,

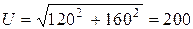где В; .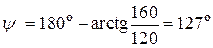

Комплекс находится во второй четверти комплексной плоскости.

Мгновенное значение напряжения

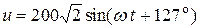, B.

В заключение рассматриваемого вопроса рекомендуем усвоить следующие очевидные равенства

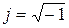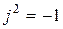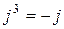; ; и т.д.

;

.

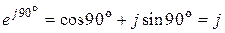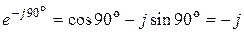Отметим, что умножение на оператор 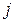означает поворот вектора на 90° про­тив часовой стрелки, а умножение на 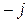означает поворот вектора на 90° по часовой стрелке.

2.4.2. Комплекс полного сопротивления и комплекс полной
проводимости. Законы Кирхгофа в комплексной форме

Отношение комплекса напряжения к комплексу тока называется комплек­сом полного сопротивления цепи

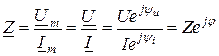. (2.41)

Модуль комплексного сопротивления равен полному сопротивлению 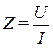, его аргумент – углу сдвига фаз 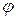. Комплексное сопротивление в алгебраи­ческой форме выглядит следующим образом

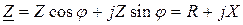. (2.42)

Следовательно, активное сопротивление есть вещественная часть, а реактив­ное – мнимая часть комплекса полного сопротивления цепи. Частные слу­чаи формулы (2.42) приведены в таблице 2.1

Таблица 2.1

Участок электрической цепи	Комплексное сопротивление

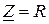
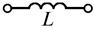
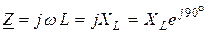
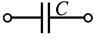
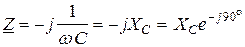
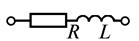
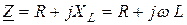
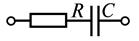
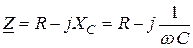
Величина, обратная комплексу полного сопротивления, называется комплек­сом полной проводимости

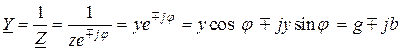, (2.43)

где 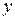, , 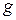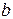– полная, активная, реактивная проводимости цепи соответственно.

Для цепей синусоидального тока законы Кирхгофа формулируются так же, как и для цепей постоянного тока, но только для комплексных значений токов и напряжений. Первый закон Кирхгофа: «алгебраическая сумма комплексов тока в узле электрической цепи равна нулю»

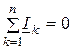. (2.44)

Второй закон Кирхгофа: «в любом замкнутом контуре электрической цепи алгебраическая сумма комплексных ЭДС равна алгебраической сумме комплекс­ных напряжений на всех пассивных элементах этого контура»

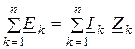. (2.45)

Таким образом, при комплексном представлении всех параметров методы расчета сложных цепей постоянного тока, основанные на законах Ома и Кирхгофа (контурных токов, узловых потенциалов, эквивалентного генератора, преобразо­вания и др.), можно применять для расчета цепей синусоидального тока.